كيفية إجراء تحليل المكونات الرئيسية في sas

تحليل المكونات الرئيسية (PCA) هو أسلوب تعلم آلي غير خاضع للرقابة يسعى إلى العثور على المكونات الرئيسية – مجموعات خطية من متغيرات التوقع – التي تفسر جزءًا كبيرًا من التباين في مجموعة البيانات.

إن أبسط طريقة لتنفيذ PCA في SAS هي استخدام عبارة PROC PRINCOMP ، التي تستخدم بناء الجملة الأساسي التالي:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

إليك ما تفعله كل تعليمات:

• البيانات : اسم مجموعة البيانات المراد استخدامها لـ PCA
• out : اسم مجموعة البيانات المراد إنشاؤها والتي تحتوي على جميع البيانات الأصلية بالإضافة إلى درجات المكون الرئيسي
• outstat : يحدد أنه يجب إنشاء مجموعة بيانات تحتوي على الوسائل والانحرافات المعيارية ومعاملات الارتباط والقيم الذاتية والمتجهات الذاتية.
• var : المتغيرات التي سيتم استخدامها لـ PCA من مجموعة بيانات الإدخال.

يوضح المثال التالي خطوة بخطوة كيفية استخدام عبارة PROC PRINCOMP عمليًا لإجراء تحليل المكونات الأساسية في SAS.

الخطوة 1: إنشاء مجموعة بيانات

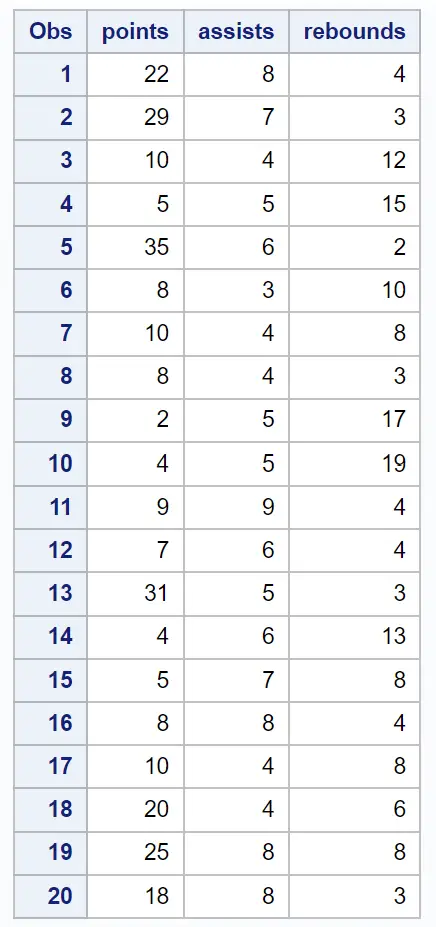
لنفترض أن لدينا مجموعة البيانات التالية التي تحتوي على معلومات متنوعة حول 20 لاعب كرة سلة:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

الخطوة 2: إجراء تحليل المكونات الرئيسية

يمكننا استخدام عبارة PROC PRINCOMP لإجراء تحليل المكون الرئيسي باستخدام متغيرات النقاط والمساعدات والارتدادات في مجموعة البيانات:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

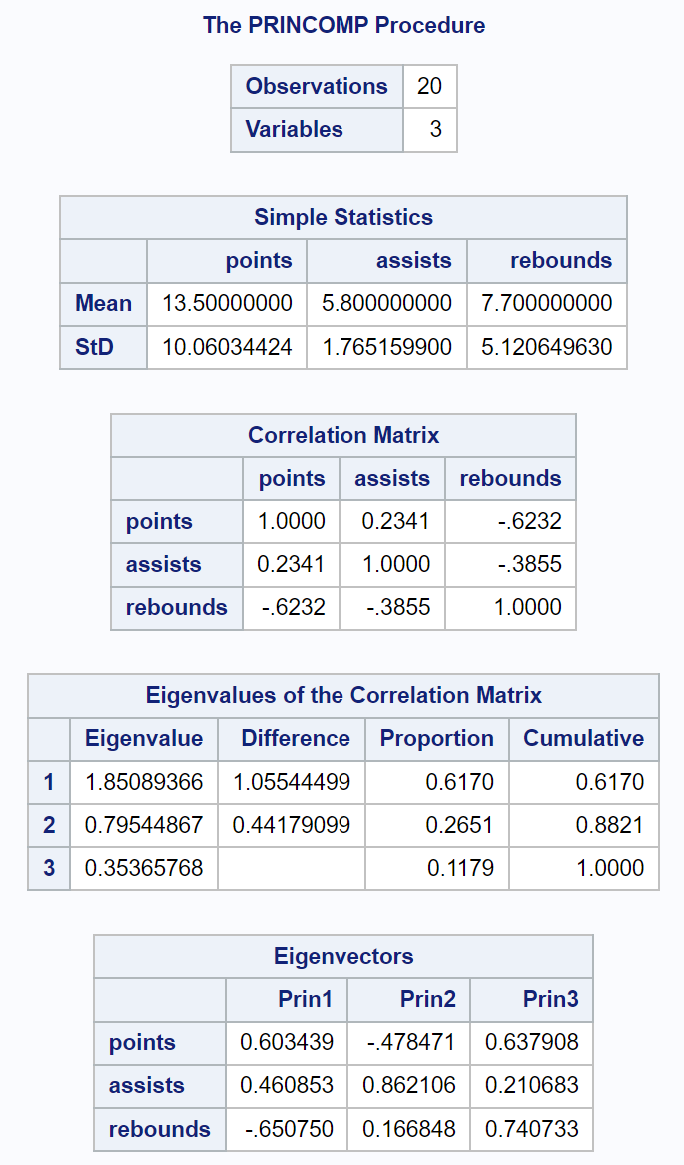
يعرض الجزء الأول من الإخراج إحصائيات وصفية مختلفة، بما في ذلك المتوسطات والانحرافات المعيارية لكل متغير إدخال، ومصفوفة الارتباط، وقيم القيم الذاتية والمتجهات الذاتية:

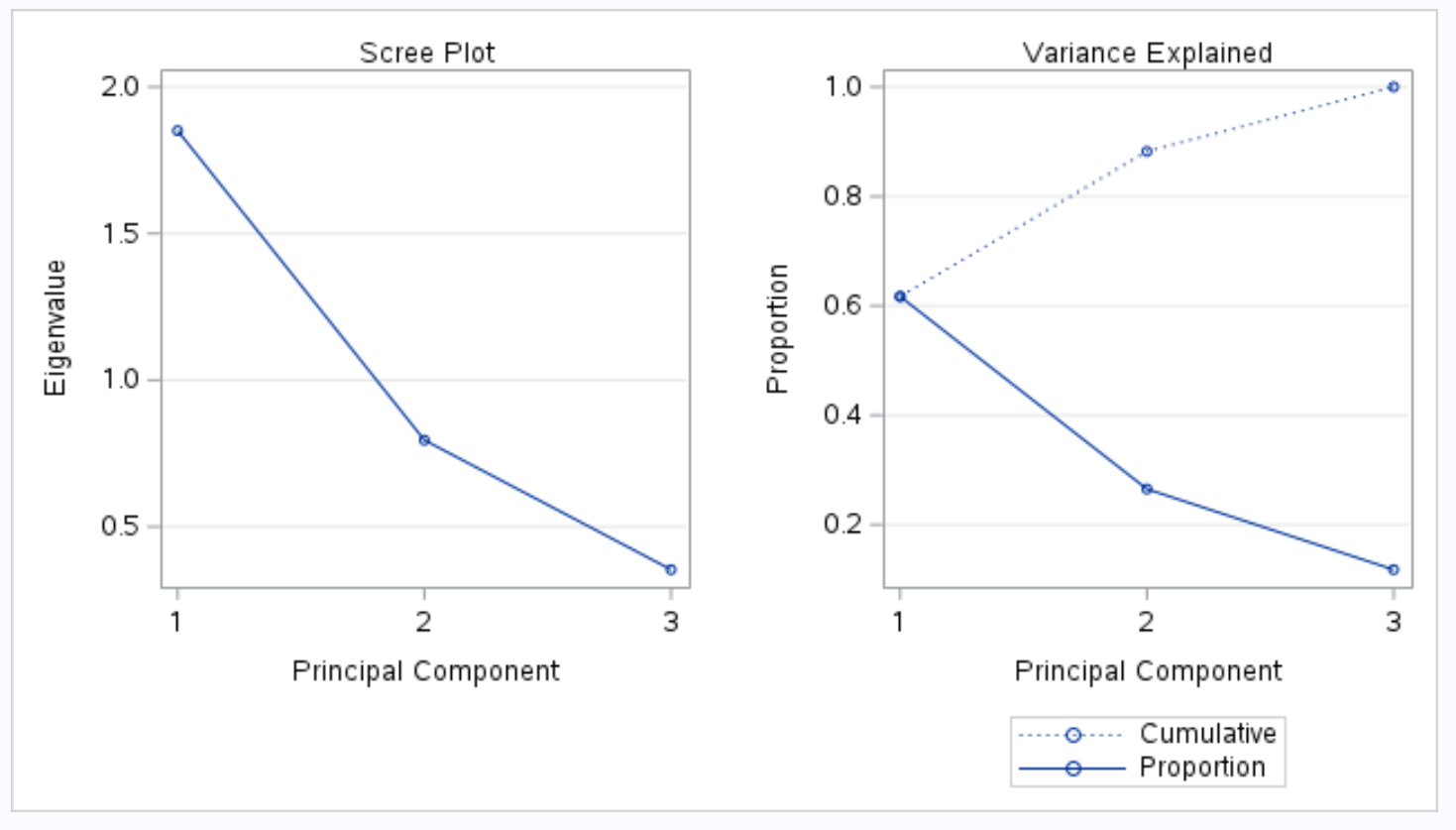
يعرض الجزء التالي من الإخراج مخططًا متماسكًا ومؤامرة تباين موضحة :

عندما نقوم بإجراء PCA، غالبًا ما نريد أن نفهم النسبة المئوية للتباين الإجمالي في مجموعة البيانات التي يمكن تفسيرها بواسطة كل مكون رئيسي.

يتيح لنا الجدول الناتج الذي يحمل عنوان القيم الذاتية لمصفوفة الارتباط معرفة النسبة المئوية للتباين الإجمالي الذي يفسره كل مكون رئيسي:

• يشرح المكون الرئيسي الأول 61.7% من إجمالي التباين في مجموعة البيانات.
• ويشرح المكون الرئيسي الثاني 26.51% من إجمالي التباين في مجموعة البيانات.
• ويشرح المكون الرئيسي الثالث 11.79% من إجمالي التباين في مجموعة البيانات.

لاحظ أن جميع النسب المئوية تصل إلى 100%.

تسمح لنا الحبكة التي تحمل عنوان “شرح التباين” بتصور هذه القيم.

يعرض المحور السيني المكون الرئيسي ويعرض المحور الصادي النسبة المئوية لإجمالي التباين الموضح بواسطة كل مكون رئيسي فردي.

الخطوة 3: قم بإنشاء مخطط ثنائي لتصور النتائج

لتصور نتائج PCA لمجموعة بيانات معينة، يمكننا إنشاء مخطط ثنائي ، وهو مخطط يعرض كل ملاحظة في مجموعة بيانات على مستوى يتكون من أول مكونين رئيسيين.

يمكننا استخدام بناء الجملة التالي في SAS لإنشاء مخطط ثنائي:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

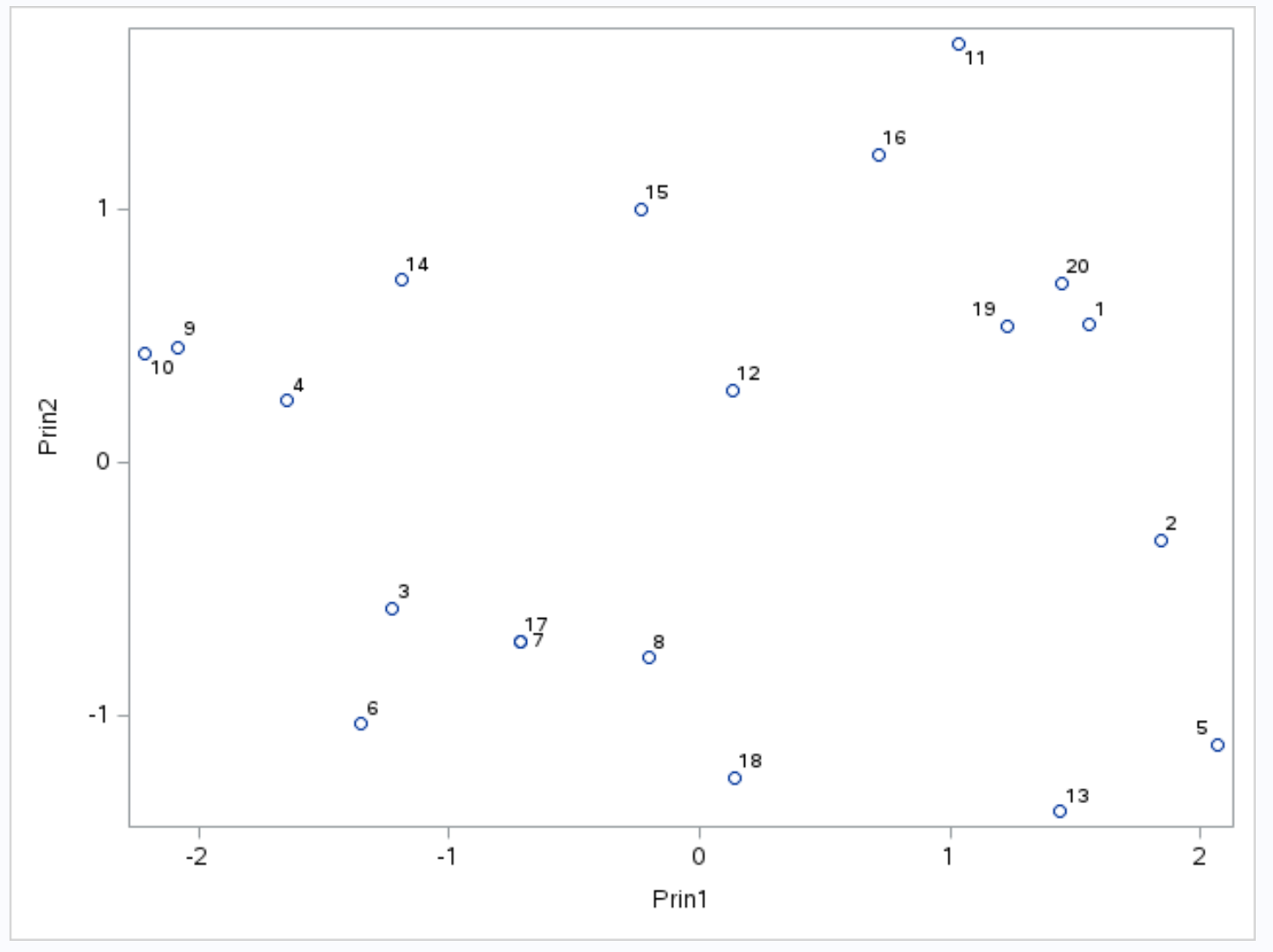
يعرض المحور السيني المكون الرئيسي الأول، ويعرض المحور الصادي المكون الرئيسي الثاني، ويتم عرض الملاحظات الفردية من مجموعة البيانات داخل الرسم البياني كدوائر صغيرة.

الملاحظات التي تكون جنبًا إلى جنب على الرسم البياني لها قيم مماثلة للمتغيرات الثلاثة من النقاط والتمريرات والمرتدات .

على سبيل المثال، في أقصى يسار الرسم البياني، يمكننا أن نرى أن الملاحظات رقم 9 ورقم 10 قريبة جدًا من بعضها البعض.

إذا عدنا إلى مجموعة البيانات الأصلية، يمكننا أن نرى القيم التالية لهذه الملاحظات:

• الملاحظة رقم 9 : 2 نقطة، 5 تمريرات حاسمة، 17 كرة مرتدة
• الملاحظة رقم 10 : 4 نقاط، 5 تمريرات حاسمة، 19 كرة مرتدة

القيم متشابهة لكل من المتغيرات الثلاثة، وهو ما يفسر سبب قرب هذه الملاحظات من بعضها البعض على المخطط الثنائي.

ورأينا أيضًا في جدول النتائج الذي يحمل عنوان القيم الذاتية لمصفوفة الارتباط أن المكونين الرئيسيين الأولين يمثلان 88.21% من إجمالي التباين في مجموعة البيانات.

نظرًا لأن هذه النسبة مرتفعة جدًا، فمن الصحيح تحليل الملاحظات في المخطط الثنائي القريبة من بعضها البعض، لأن المكونين الرئيسيين اللذين يشكلان المخطط الثنائي يمثلان تقريبًا جميع الاختلافات في مجموعة البيانات.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في SAS:

كيفية إجراء الانحدار الخطي البسيط في SAS
كيفية إجراء الانحدار الخطي المتعدد في SAS
كيفية إجراء الانحدار اللوجستي في SAS