ما هو التحليل أحادي المتغير؟ (التعريف & #038؛ مثال)

يشير مصطلح التحليل أحادي المتغير إلى تحليل متغير واحد. يمكنك تذكر ذلك لأن البادئة “uni” تعني “واحد”.

الهدف من التحليل أحادي المتغير هو فهم توزيع القيم لمتغير واحد. ويمكن مقارنة هذا النوع من التحليل بما يلي:

• التحليل ثنائي المتغير : تحليل متغيرين.
• التحليل متعدد المتغيرات: تحليل متغيرين أو أكثر.

على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية:

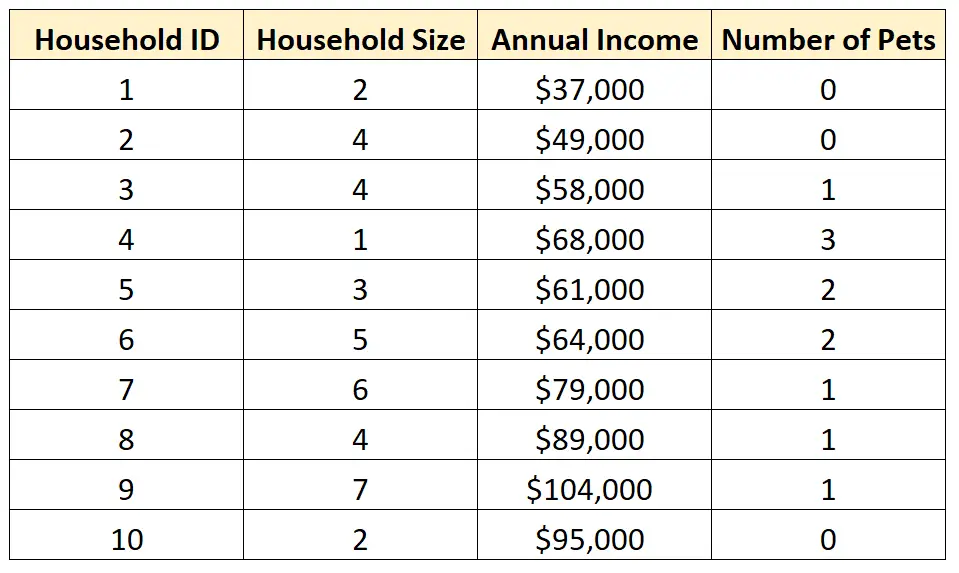
قد نختار إجراء تحليل أحادي المتغير على أحد المتغيرات الفردية في مجموعة البيانات لفهم توزيع القيم بشكل أفضل.

على سبيل المثال، يمكننا اختيار إجراء تحليل أحادي المتغير على المتغير حجم الأسرة :

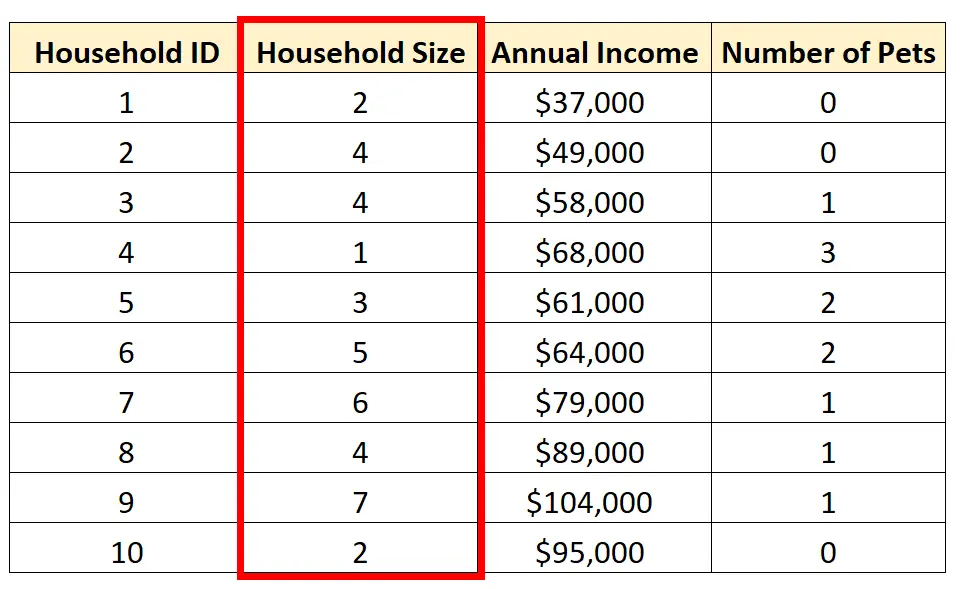
هناك ثلاث طرق شائعة لإجراء التحليل أحادي المتغير:

1. إحصائيات موجزة

الطريقة الأكثر شيوعًا لإجراء التحليل أحادي المتغير هي وصف متغير باستخدام إحصائيات الملخص .

هناك نوعان شائعان من الإحصائيات الموجزة:

• مقاييس النزعة المركزية : تصف هذه الأرقام مكان مركز مجموعة البيانات. وتشمل الأمثلة المتوسط والوسيط .
• مقاييس التشتت : تصف هذه الأرقام توزيع القيم في مجموعة البيانات. تتضمن الأمثلة الفاصل الزمني والمدى الربيعي والانحراف المعياري والتباين .

2. توزيعات التردد

هناك طريقة أخرى لإجراء تحليل أحادي المتغير وهي إنشاء توزيع تكراري يصف عدد مرات ظهور قيم مختلفة في مجموعة البيانات.

3. الرسومات

هناك طريقة أخرى لإجراء التحليل أحادي المتغير وهي إنشاء رسوم بيانية لتصور توزيع القيم لمتغير معين.

تشمل الأمثلة الشائعة ما يلي:

• بوكسبلوتس
• الرسوم البيانية
• منحنيات الكثافة
• كاممبرت

توضح الأمثلة التالية كيفية إجراء كل نوع من التحليل أحادي المتغير باستخدام متغير حجم الأسرة من مجموعة البيانات المذكورة سابقًا:

احصائيات ملخصة

يمكننا حساب المقاييس التالية للاتجاه المركزي لحجم الأسرة:

• المتوسط (متوسط القيمة): 3.8
• الوسيط (القيمة المتوسطة): 4

تعطينا هذه القيم فكرة عن مكان وجود القيمة “المركزية”.

يمكننا أيضًا حساب مقاييس التشتت التالية:

• النطاق (الفرق بين الحد الأقصى والحد الأدنى): 6
• المقياس الرباعي (توزيع الـ 50% الوسطى من القيم): 2.5
• الانحراف المعياري (مقياس متوسط الانتشار): 1.87

هذه القيم تعطينا فكرة عن توزيع قيم هذا المتغير.

التوزيع بتكرار

يمكننا أيضًا إنشاء جدول التوزيع التكراري التالي لتلخيص عدد مرات ظهور القيم المختلفة:

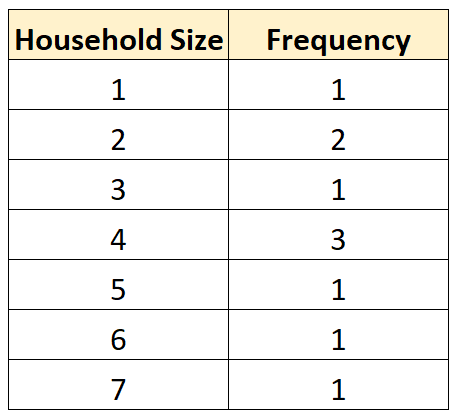
يتيح لنا هذا أن نرى بسرعة أن حجم الأسرة الأكثر شيوعًا هو 4 أشخاص .

المصدر: يمكنك استخدام حاسبة التكرار هذه لإنتاج توزيع تكراري لأي متغير تلقائيًا.

الرسومات

يمكننا إنشاء الرسوم البيانية التالية لمساعدتنا في تصور توزيع القيم لحجم الأسرة:

1. بوكسبلوت

Boxplot هو رسم بياني يعرض ملخصًا مكونًا من خمسة أرقام لمجموعة بيانات.

يتضمن ملخص الأرقام الخمسة ما يلي:

• الحد الأدنى للقيمة
• الربع الأول
• القيمة المتوسطة
• الربع الثالث
• القيمة القصوى

إليك ما سيبدو عليه مخطط boxplot لمتغير حجم الأسرة:

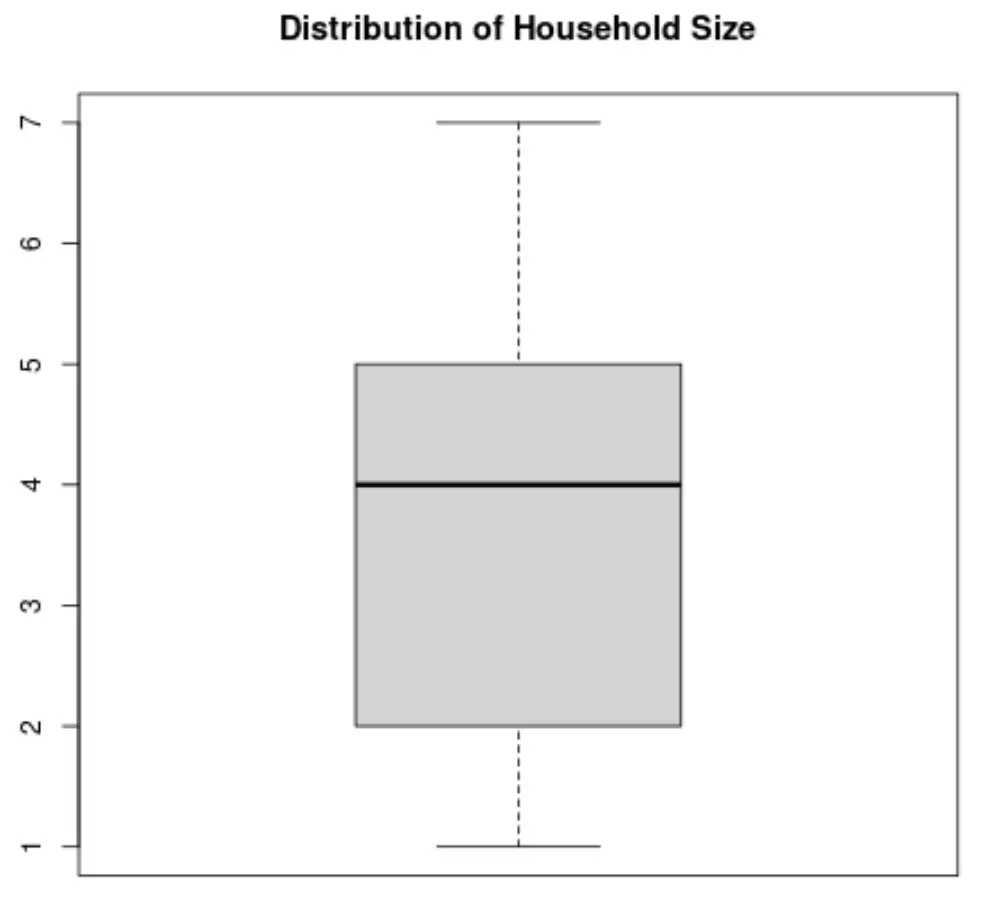
المصدر: يمكنك استخدام منشئ boxplot هذا لإنتاج boxplot تلقائيًا لأي متغير.

2. الرسم البياني

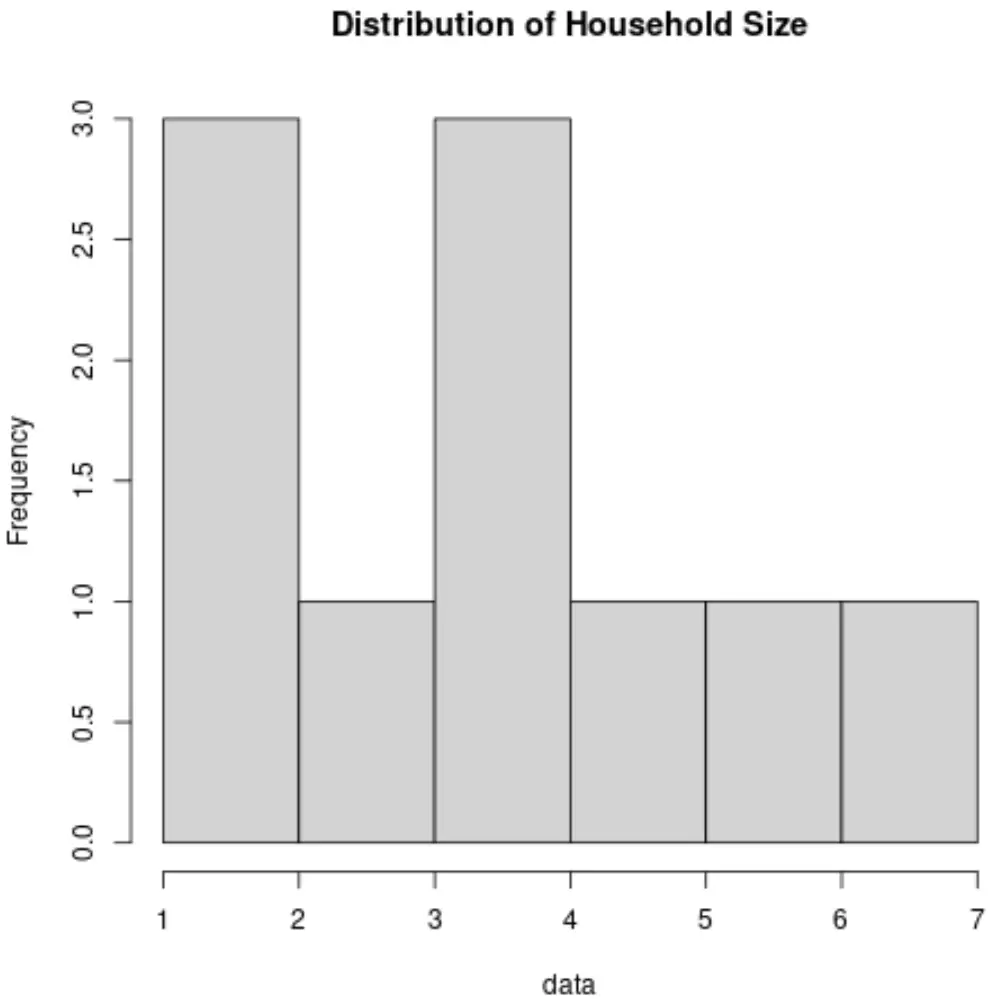
الرسم البياني هو نوع من المخططات التي تستخدم أشرطة عمودية لعرض الترددات. يعد هذا النوع من المخططات طريقة مفيدة لتصور توزيع القيم في مجموعة البيانات.

هذا هو الشكل الذي سيبدو عليه الرسم البياني لمتغير حجم الأسرة:

3. منحنى الكثافة

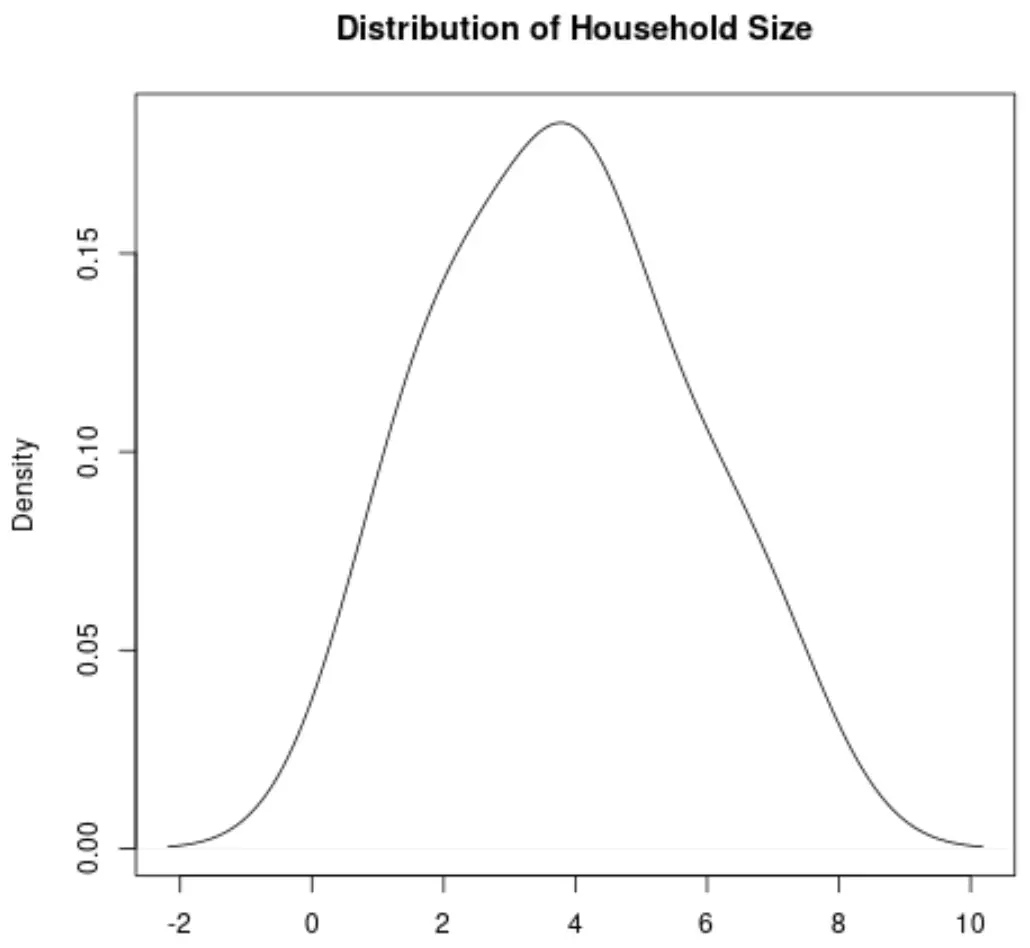
منحنى الكثافة هو منحنى على الرسم البياني الذي يمثل توزيع القيم في مجموعة من البيانات.

إنه مفيد بشكل خاص لتصور “شكل” التوزيع، بما في ذلك ما إذا كان التوزيع يحتوي على “ذروة” واحدة أو أكثر من القيم المتكررة أم لا وما إذا كان التوزيع منحرفًا إلى اليسار أو اليمين أم لا .

إليك الشكل الذي سيبدو عليه منحنى الكثافة لمتغير حجم الأسرة:

4. الرسم البياني الدائري

المخطط الدائري هو نوع من المخططات على شكل دائرة ويستخدم شرائح لتمثيل نسب الكل.

إليك ما سيبدو عليه المخطط الدائري لمتغير حجم الأسرة:

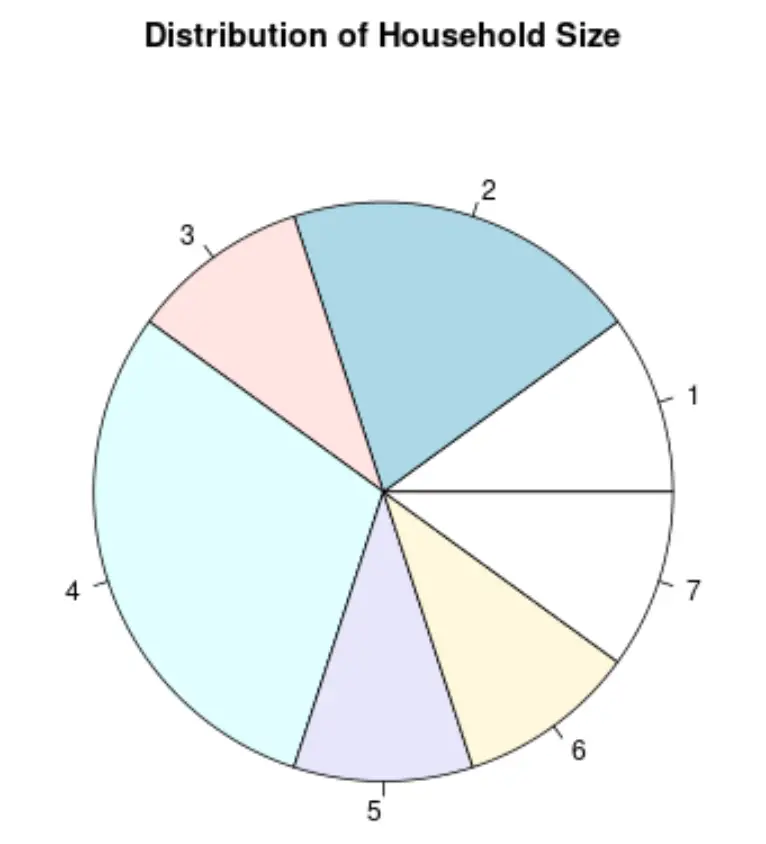
اعتمادًا على نوع البيانات، قد يكون أحد هذه المخططات أكثر فائدة من المخططات الأخرى لتصور توزيع القيم.