كيفية إجراء تحليل ثنائي المتغير في بايثون: مع أمثلة

يشير مصطلح التحليل ثنائي المتغير إلى تحليل متغيرين. يمكنك تذكر ذلك لأن البادئة “bi” تعني “اثنين”.

الهدف من التحليل ثنائي المتغير هو فهم العلاقة بين متغيرين

هناك ثلاث طرق شائعة لإجراء التحليل ثنائي المتغير:

1. نقطة الغيوم

2. معاملات الارتباط

3. الانحدار الخطي البسيط

يوضح المثال التالي كيفية إجراء كل نوع من هذه الأنواع من التحليل ثنائي المتغير في بايثون باستخدام الباندا التالية DataFrame التي تحتوي على معلومات حول متغيرين: (1) الساعات التي تم قضاؤها في الدراسة و (2) درجة الامتحان التي حصل عليها 20 طالبًا مختلفًا:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. نقطة الغيوم

يمكننا استخدام الصيغة التالية لإنشاء مخطط مبعثر لساعات الدراسة مقابل نتائج الامتحان:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

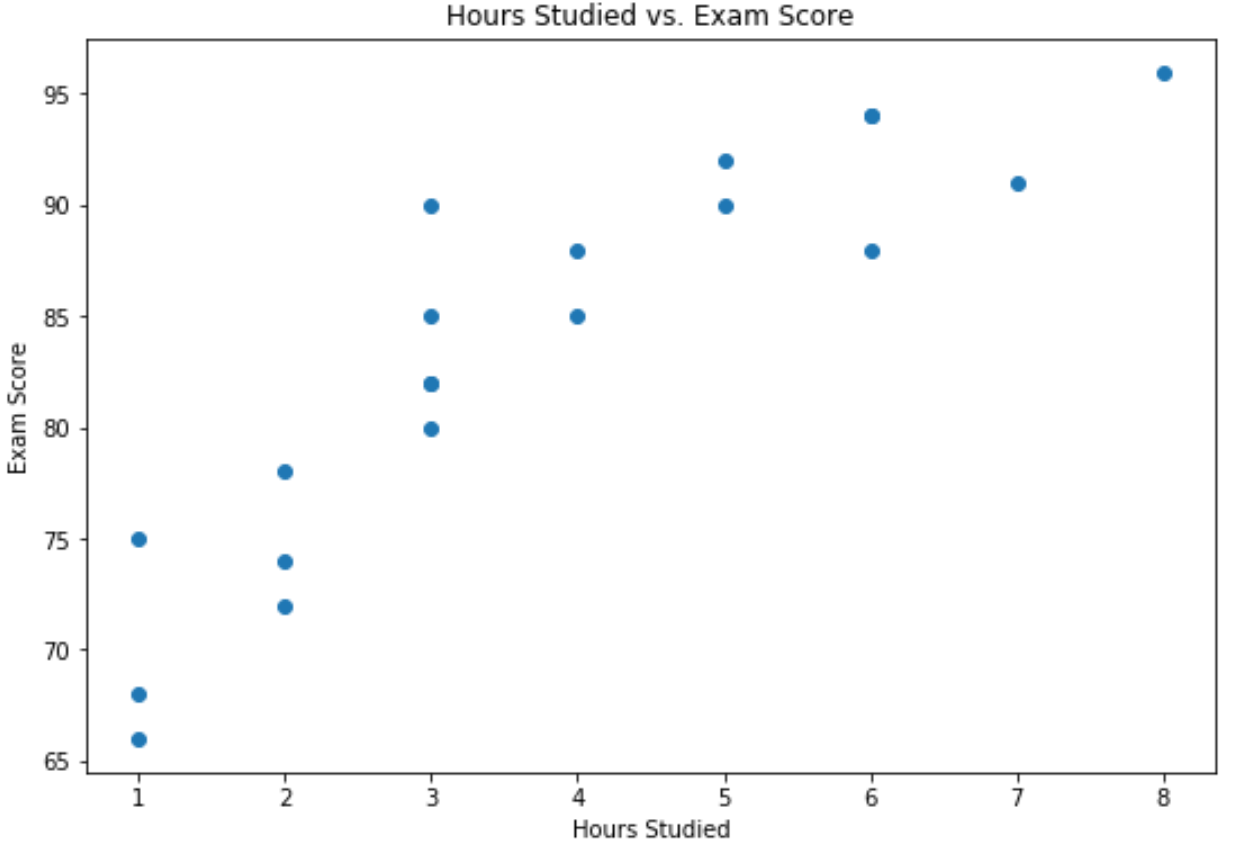
يُظهر المحور “س” الساعات التي تمت دراستها، بينما يُظهر المحور “ص” الدرجة التي تم الحصول عليها في الاختبار.

ويبين الرسم البياني أن هناك علاقة إيجابية بين المتغيرين: فكلما زاد عدد ساعات الدراسة، تميل درجات الامتحانات أيضا إلى الارتفاع.

2. معاملات الارتباط

معامل ارتباط بيرسون هو وسيلة لقياس العلاقة الخطية بين متغيرين.

يمكننا استخدام الدالة corr() في الباندا لإنشاء مصفوفة الارتباط:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

وتبين أن معامل الارتباط هو 0.891 . ويشير هذا إلى وجود علاقة إيجابية قوية بين ساعات الدراسة ودرجة الامتحان.

3. الانحدار الخطي البسيط

الانحدار الخطي البسيط هو طريقة إحصائية يمكننا استخدامها لتحديد العلاقة بين متغيرين.

يمكننا استخدام الدالة OLS() من حزمة statsmodels لملاءمة نموذج الانحدار الخطي البسيط بسرعة لساعات الدراسة ونتائج الامتحانات المستلمة:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

وتبين أن معادلة الانحدار المجهزة هي:

درجة الامتحان = 69.0734 + 3.8471*(ساعات الدراسة)

وهذا يخبرنا أن كل ساعة إضافية تتم دراستها ترتبط بمتوسط زيادة قدرها 3.8471 في درجة الامتحان.

يمكننا أيضًا استخدام معادلة الانحدار المجهزة للتنبؤ بالنتيجة التي سيحصل عليها الطالب بناءً على إجمالي عدد الساعات المدروسة.

على سبيل المثال الطالب الذي يدرس لمدة 3 ساعات يجب أن يحصل على 81.6147 :

• درجة الامتحان = 69.0734 + 3.8471*(ساعات الدراسة)
• درجة الامتحان = 69.0734 + 3.8471*(3)
• نتيجة الامتحان = 81.6147

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول التحليل ثنائي المتغير:

مقدمة للتحليل ثنائي المتغير
5 أمثلة للبيانات ثنائية المتغير في الحياة الحقيقية
مقدمة للانحدار الخطي البسيط
مقدمة لمعامل ارتباط بيرسون