كيفية تحويل البيانات في بايثون (السجل، الجذر التربيعي، الجذر التكعيبي)

تفترض العديد من الاختبارات الإحصائية أن مجموعات البيانات يتم توزيعها بشكل طبيعي. ومع ذلك، هذا ليس هو الحال في كثير من الأحيان في الممارسة العملية.

إحدى طرق حل هذه المشكلة هي تحويل توزيع القيم في مجموعة بيانات باستخدام أحد التحويلات الثلاثة:

1. تحويل السجل: تحويل متغير الاستجابة من y إلى log(y) .

2. تحويل الجذر التربيعي: تحويل متغير الاستجابة من y إلى √y .

3. تحويل الجذر التكعيبي: تحويل متغير الاستجابة من y إلى y ^1/3 .

ومن خلال إجراء هذه التحويلات، تصبح مجموعة البيانات موزعة بشكل طبيعي أكثر.

توضح الأمثلة التالية كيفية تنفيذ هذه التحويلات في بايثون.

تحويل السجل في بيثون

يوضح التعليمة البرمجية التالية كيفية إجراء تحويل لوغاريتمي على متغير وإنشاء مخططات جنبًا إلى جنب لعرض التوزيع الأصلي وتوزيع البيانات المحولة بالسجل:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 4 , b= 15 , size= 300 )

#create log-transformed data
data_log = np. log (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Log-Transformed Data ')

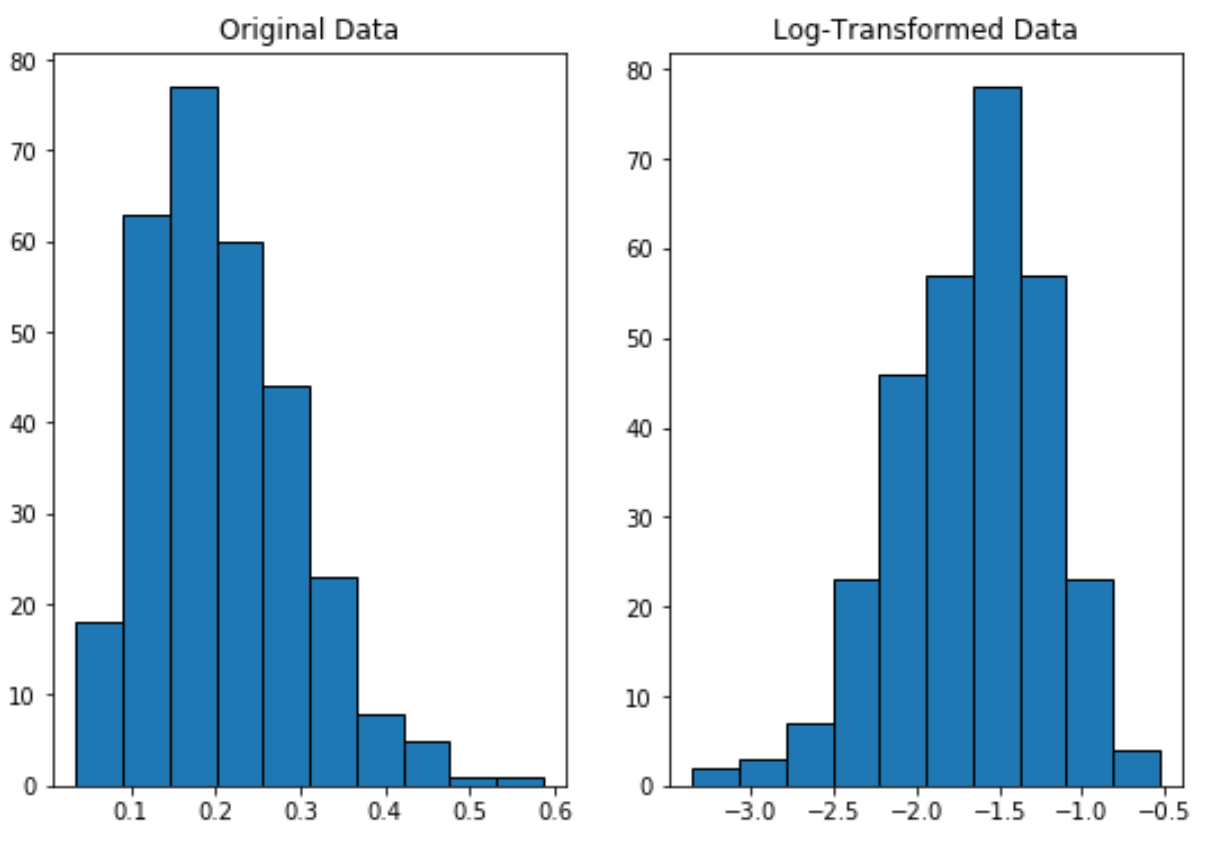
لاحظ كيف يتم توزيع التوزيع المحول بالسجل بشكل طبيعي أكثر من التوزيع الأصلي.

لا يزال “شكل الجرس” غير مثالي ولكنه أقرب إلى التوزيع الطبيعي من التوزيع الأصلي.

تحويل الجذر التربيعي في بايثون

يوضح التعليمة البرمجية التالية كيفية إجراء تحويل الجذر التربيعي على متغير وإنشاء مخططات جنبًا إلى جنب لعرض التوزيع الأصلي وتوزيع الجذر التربيعي المحول للبيانات:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. sqrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Square Root Transformed Data ') 

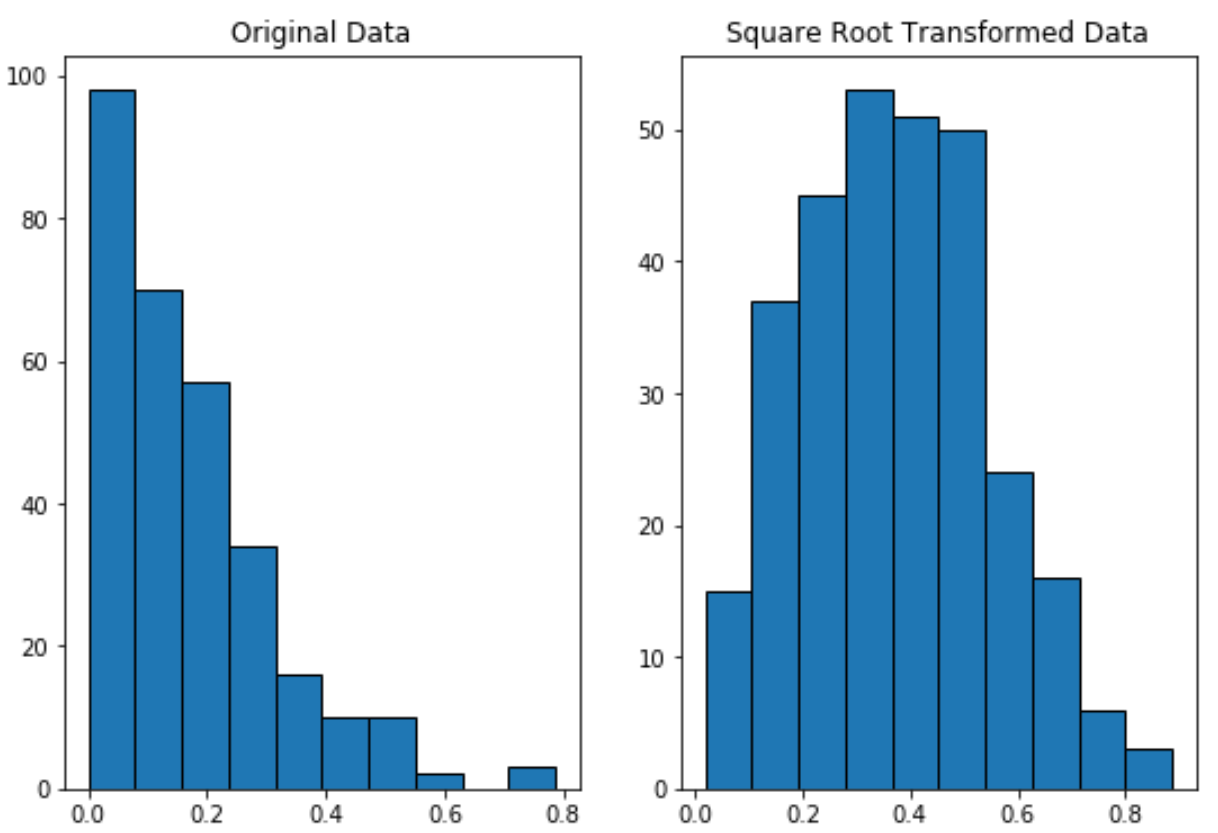
لاحظ كيف يتم توزيع البيانات المحولة بالجذر التربيعي بشكل طبيعي أكثر من البيانات الأصلية.

تحويل الجذر التكعيبي في بايثون

يوضح التعليمة البرمجية التالية كيفية إجراء تحويل الجذر التكعيبي على متغير وإنشاء مخططات جنبًا إلى جنب لعرض التوزيع الأصلي وتوزيع الجذر المكعب المحول للبيانات:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. cbrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Cube Root Transformed Data ') 

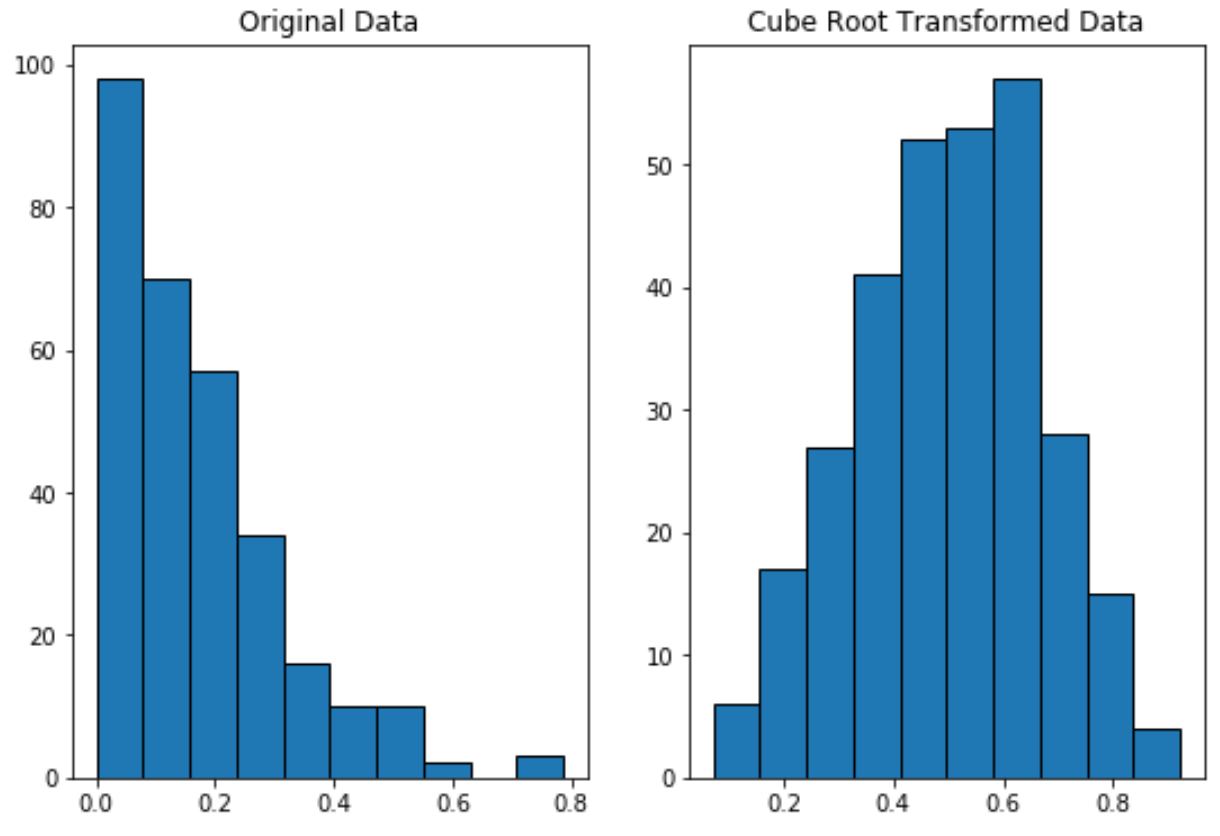
لاحظ كيف يتم توزيع البيانات المحولة بالجذر التكعيبي بشكل طبيعي أكثر من البيانات الأصلية.

مصادر إضافية

كيفية حساب درجات Z في بايثون
كيفية تطبيع البيانات في بايثون
ما هو الافتراض الطبيعي في الإحصاء؟