كيفية إجراء تحويل box-cox في بايثون

يعد تحويل box-cox طريقة شائعة الاستخدام لتحويل مجموعة بيانات غير موزعة بشكل طبيعي إلى مجموعة موزعة بشكل طبيعي .

الفكرة الأساسية وراء هذه الطريقة هي إيجاد قيمة لـ lect بحيث تكون البيانات المحولة قريبة قدر الإمكان من التوزيع الطبيعي، باستخدام الصيغة التالية:

• y() = (y ^ – 1) /  إذا y ≠ 0
• y(lect) = log(y) إذا كانت y = 0

يمكننا إجراء تحويل box-cox في بايثون باستخدام الدالة scipy.stats.boxcox() .

يوضح المثال التالي كيفية استخدام هذه الوظيفة عمليًا.

مثال: تحويل Box-Cox في بايثون

لنفترض أننا قمنا بإنشاء مجموعة عشوائية مكونة من 1000 قيمة من التوزيع الأسي :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

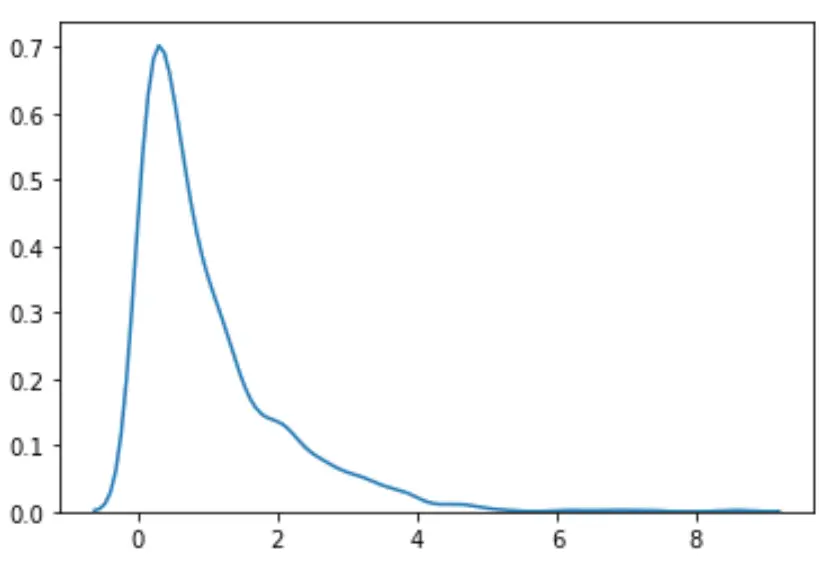
يمكننا أن نرى أن التوزيع لا يبدو طبيعيا.

يمكننا استخدام الدالة boxcox() ‎ للعثور على القيمة المثلى لـ lambda التي تنتج توزيعًا أكثر طبيعية:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

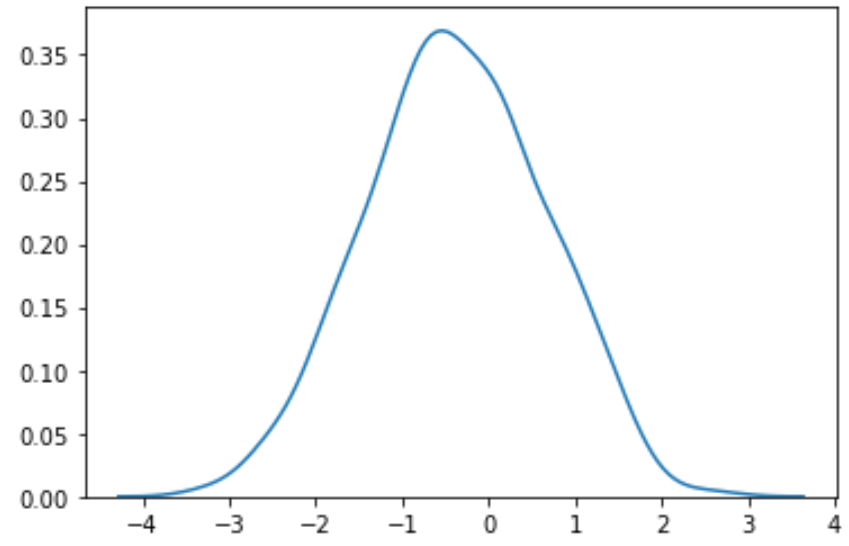
يمكننا أن نرى أن البيانات المحولة تتبع توزيعًا طبيعيًا أكثر بكثير.

يمكننا أيضًا العثور على قيمة لامدا الدقيقة المستخدمة لإجراء تحويل Box-Cox:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

تم العثور على لامدا الأمثل ليكون حوالي 0.242 .

وبالتالي، تم تحويل كل قيمة بيانات باستخدام المعادلة التالية:

الجديد = (القديم ^0.242 – 1) / 0.242

يمكننا التأكد من ذلك من خلال النظر إلى قيم البيانات الأصلية مقابل البيانات المحولة:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

القيمة الأولى في مجموعة البيانات الأصلية كانت 0.79587 . لذلك، قمنا بتطبيق الصيغة التالية لتحويل هذه القيمة:

جديد = (.79587 ^0.242 – 1) / 0.242 = -0.222

يمكننا أن نؤكد أن القيمة الأولى في مجموعة البيانات المحولة هي بالفعل -0.222 .

مصادر إضافية

كيفية إنشاء وتفسير مؤامرة QQ في بايثون
كيفية إجراء اختبار الحالة الطبيعية لشابيرو ويلك في بايثون