مقدمة لانحدار ريدج

في الانحدار الخطي المتعدد العادي، نستخدم مجموعة من متغيرات التوقع p ومتغير الاستجابة لتناسب نموذج النموذج:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

ذهب:

• Y : متغير الاستجابة
• X _j : ^{المتغير} التنبئي j
• β _j : متوسط التأثير على Y لزيادة وحدة واحدة في X _j ، مع تثبيت جميع المتنبئات الأخرى
• ε : مصطلح الخطأ

يتم اختيار قيم β ₀ , β ₁ , B ₂ , …, β _p باستخدام طريقة المربعات الصغرى التي تقلل مجموع مربعات البقايا (RSS):

RSS = Σ(y _i – ŷ _i ) ²

ذهب:

• Σ : رمز يوناني معناه المجموع
• y _i : قيمة الاستجابة الفعلية للملاحظة ^{رقم i}
• ŷ _i : قيمة الاستجابة المتوقعة بناءً على نموذج الانحدار الخطي المتعدد

ومع ذلك، عندما تكون متغيرات التوقع مترابطة بشكل كبير، يمكن أن تصبح العلاقة الخطية المتعددة مشكلة. وهذا يمكن أن يجعل تقديرات معامل النموذج غير موثوقة وتظهر تباينًا كبيرًا.

إحدى الطرق للتغلب على هذه المشكلة دون إزالة بعض المتغيرات المتوقعة من النموذج بشكل كامل هي استخدام طريقة تعرف باسم انحدار التلال ، والتي تسعى بدلاً من ذلك إلى تقليل ما يلي:

آر إس إس + Σβ _ي ²

حيث ينتقل j من 1 إلى p و ≥ ≥ 0.

يُعرف هذا الحد الثاني في المعادلة بعقوبة الانسحاب .

عندما تساوي 0 = 0، فإن مصطلح العقوبة هذا ليس له أي تأثير وينتج عن انحدار التلال نفس تقديرات المعامل مثل المربعات الصغرى. ومع ذلك، مع اقتراب π من اللانهاية، تصبح عقوبة الانكماش أكثر تأثيرًا وتقترب تقديرات معامل انحدار الذروة من الصفر.

بشكل عام، فإن المتغيرات المتوقعة الأقل تأثيرًا في النموذج سوف تنخفض نحو الصفر بشكل أسرع.

لماذا استخدام ريدج الانحدار؟

ميزة انحدار ريدج على انحدار المربعات الصغرى هي مقايضة التحيز والتباين .

تذكر أن متوسط مربع الخطأ (MSE) هو مقياس يمكننا استخدامه لقياس دقة نموذج معين ويتم حسابه على النحو التالي:

MSE = فار( f̂( x ₀ ) ) + [التحيز( f̂( x ₀ )))] ² + فار(ε)

MSE = التباين + الانحياز ² + خطأ غير قابل للاختزال

الفكرة الأساسية لانحدار ريدج هي تقديم انحياز صغير بحيث يمكن تقليل التباين بشكل كبير، مما يؤدي إلى انخفاض إجمالي المشروعات الصغيرة والمتوسطة.

لتوضيح ذلك، انظر إلى الرسم البياني التالي:

لاحظ أنه مع زيادة π، يتناقص التباين بشكل ملحوظ مع زيادة طفيفة جدًا في الانحياز. ومع ذلك، بعد نقطة معينة، يتناقص التباين بسرعة أقل ويؤدي انخفاض المعاملات إلى التقليل بشكل كبير من تقديرها، مما يؤدي إلى زيادة حادة في التحيز.

يمكننا أن نرى من الرسم البياني أن MSE للاختبار هو الأدنى عندما نختار قيمة π التي تنتج مفاضلة مثالية بين التحيز والتباين.

عندما تكون 0 = 0، فإن الحد الجزائي في انحدار التلال ليس له أي تأثير وبالتالي ينتج نفس تقديرات المعامل مثل المربعات الصغرى. ومع ذلك، من خلال زيادة π إلى نقطة معينة، يمكننا تقليل MSE الإجمالي للاختبار.

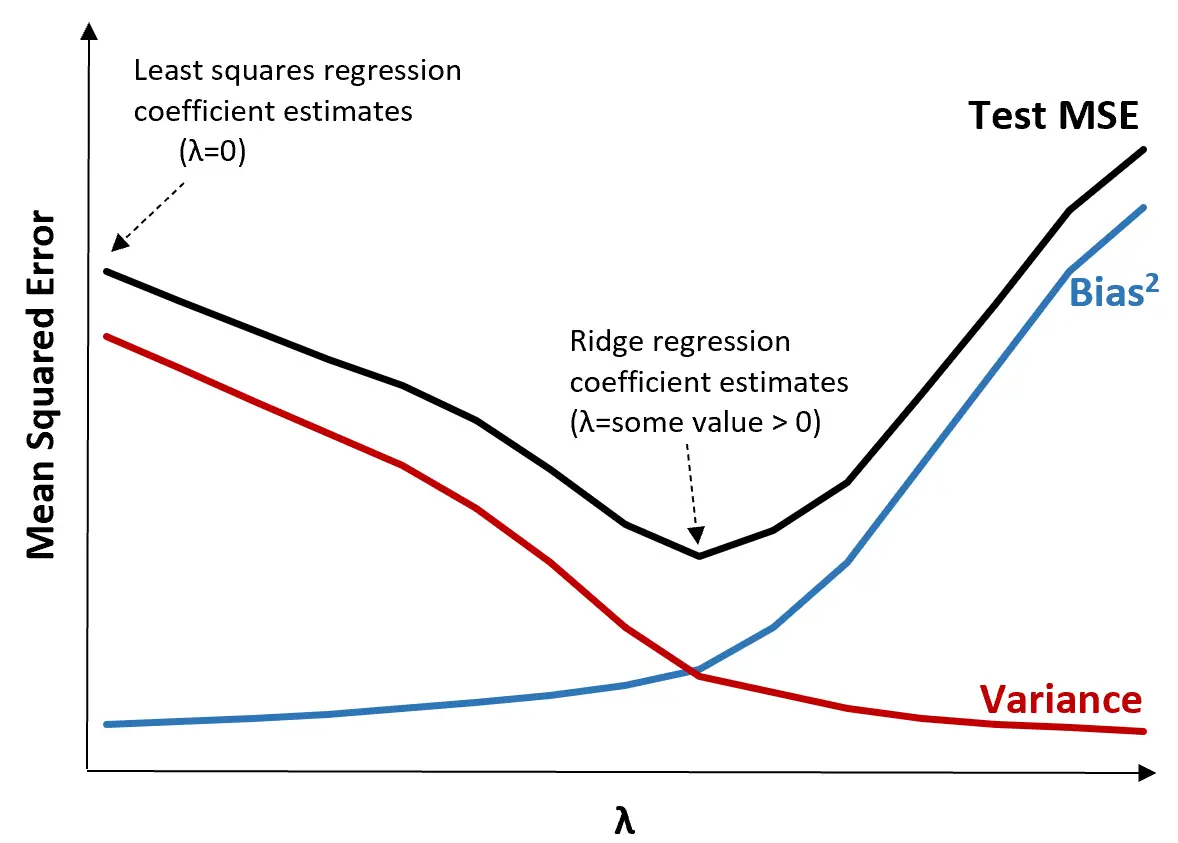
وهذا يعني أن ملاءمة النموذج عن طريق انحدار التلال سوف تنتج أخطاء اختبار أصغر من ملاءمة النموذج عن طريق انحدار المربعات الصغرى.

خطوات تنفيذ انحدار ريدج في الممارسة العملية

يمكن استخدام الخطوات التالية لإجراء انحدار التلال:

الخطوة 1: حساب مصفوفة الارتباط وقيم VIF لمتغيرات التوقع.

أولاً، نحتاج إلى إنتاج مصفوفة ارتباط وحساب قيم VIF (عامل تضخم التباين) لكل متغير متنبئ.

إذا اكتشفنا وجود علاقة قوية بين متغيرات التوقع وقيم VIF العالية (تعرف بعض النصوص قيمة VIF “العالية” على أنها 5 بينما يستخدم البعض الآخر 10)، فمن المحتمل أن يكون انحدار التلال مناسبًا.

ومع ذلك، إذا لم يكن هناك علاقة خطية متعددة في البيانات، فقد لا يكون من الضروري إجراء انحدار التلال في المقام الأول. بدلا من ذلك، يمكننا إجراء الانحدار العادي للمربعات الصغرى.

الخطوة 2: توحيد كل متغير متنبئ.

قبل تنفيذ انحدار التلال، نحتاج إلى قياس البيانات بحيث يكون لكل متغير متنبئ متوسط قدره 0 وانحراف معياري قدره 1. وهذا يضمن عدم وجود متغير متنبئ واحد له تأثير مفرط عند تشغيل انحدار التلال.

الخطوة 3: قم بملاءمة نموذج انحدار التلال واختر قيمة لـ .

لا توجد صيغة محددة يمكننا استخدامها لتحديد القيمة التي يجب استخدامها لـ lect. من الناحية العملية، هناك طريقتان شائعتان لاختيار π:

(1) قم بإنشاء مخطط تتبع ريدج. هذا رسم بياني يصور قيم تقديرات المعامل مع زيادة π نحو اللانهاية. عادة، نختار π باعتبارها القيمة التي تبدأ عندها معظم تقديرات المعاملات في الاستقرار.

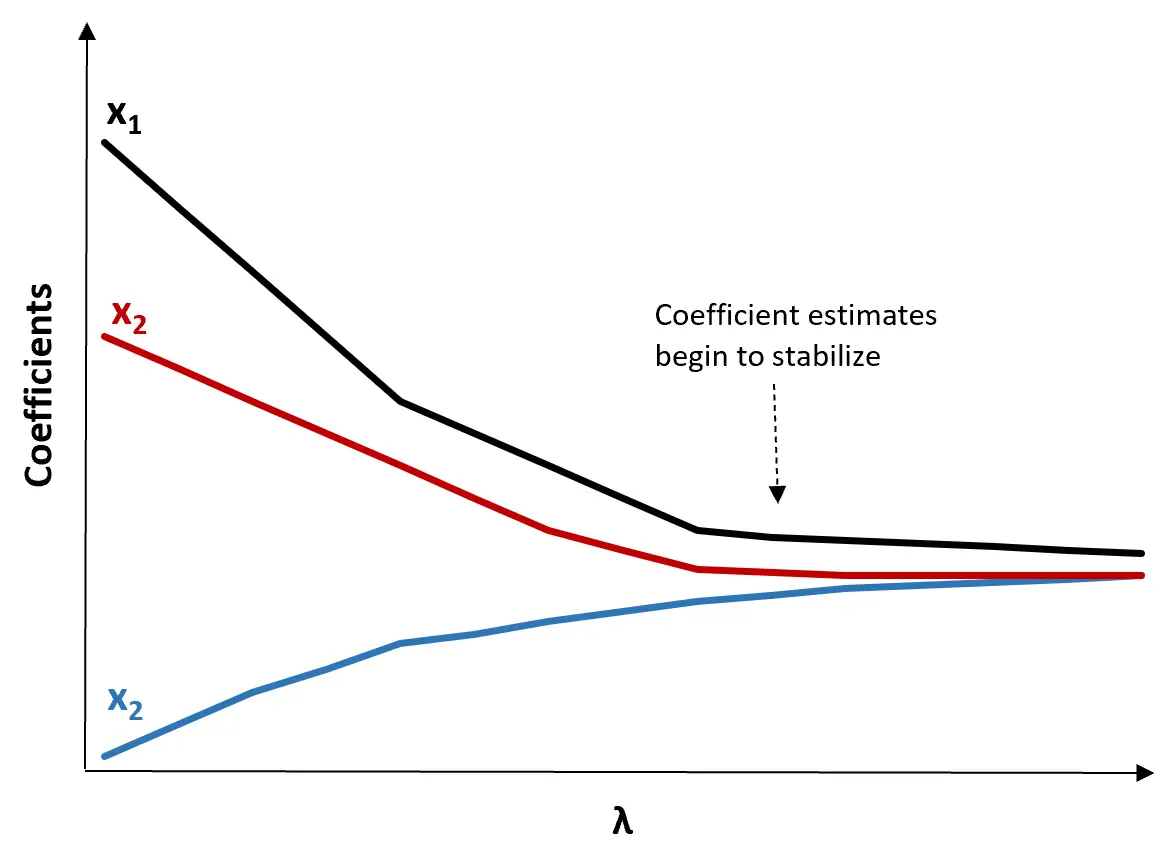
(2) احسب اختبار MSE لكل قيمة π.

هناك طريقة أخرى لاختيار π وهي ببساطة حساب اختبار MSE لكل نموذج بقيم مختلفة لـ π واختيار π لتكون القيمة التي تنتج أدنى اختبار MSE.

مزايا وعيوب انحدار ريدج

الميزة الأكبر لانحدار ريدج هي قدرته على إنتاج متوسط خطأ مربع للاختبار (MSE) أقل من المربعات الصغرى عند وجود علاقة خطية متعددة.

ومع ذلك، فإن أكبر عيب في انحدار ريدج هو عدم قدرته على إجراء اختيار متغير لأنه يتضمن جميع المتغيرات المتوقعة في النموذج النهائي. نظرًا لأن بعض المتنبئين سيتم تخفيضهم إلى ما يقرب من الصفر، فقد يؤدي ذلك إلى صعوبة تفسير نتائج النموذج.

من الناحية العملية، يمتلك انحدار ريدج القدرة على إنتاج نموذج قادر على تقديم تنبؤات أفضل مقارنة بنموذج المربعات الصغرى، ولكن غالبًا ما يكون تفسير نتائج النموذج أكثر صعوبة.

اعتمادًا على ما إذا كان تفسير النموذج أو دقة التنبؤ أكثر أهمية بالنسبة لك، يمكنك اختيار استخدام المربعات الصغرى العادية أو انحدار التلال في سيناريوهات مختلفة.

انحدار ريدج في R & Python

تشرح البرامج التعليمية التالية كيفية إجراء انحدار التلال في لغة R وPython، وهما اللغتان الأكثر استخدامًا لنماذج انحدار التلال:

انحدار ريدج في R (خطوة بخطوة)
انحدار ريدج في بايثون (خطوة بخطوة)