Binning على قدم المساواة في بيثون

في الإحصاء، التجميع هو عملية وضع القيم الرقمية في مجموعات .

يُعرف الشكل الأكثر شيوعًا للتجميع باسم التجميع المتساوي العرض ، حيث نقوم بتقسيم مجموعة البيانات إلى مجموعات k متساوية العرض.

يُعرف أحد أشكال التجميع الأقل استخدامًا باسم التجميع المتساوي للتردد ، حيث نقسم مجموعة البيانات إلى مجموعات k ، جميعها لها عدد متساوٍ من الترددات.

يشرح هذا البرنامج التعليمي كيفية تنفيذ تجميع الترددات المتساوية في بايثون.

Binning على قدم المساواة في بيثون

لنفترض أن لدينا مجموعة بيانات تحتوي على 100 قيمة:

 import numpy as np
import matplotlib.pyplot as plt

#create data
np.random.seed(1)
data = np.random.randn(100)

#view first 5 values
data[:5]

array([ 1.62434536, -0.61175641, -0.52817175, -1.07296862, 0.86540763])

تجميع متساوي العرض:

إذا قمنا بإنشاء رسم بياني لعرض هذه القيم، فستقوم بايثون افتراضيًا بالتجميع متساوي العرض:

 #create histogram with equal-width bins
n, bins, patches = plt.hist(data, edgecolor='black')
plt.show()

#display bin boundaries and frequency per bin 
bins, n

(array([-2.3015387 , -1.85282729, -1.40411588, -0.95540447, -0.50669306,
        -0.05798165, 0.39072977, 0.83944118, 1.28815259, 1.736864,
         2.18557541]),
 array([ 3., 1., 6., 17., 19., 20., 14., 12., 5., 3.]))

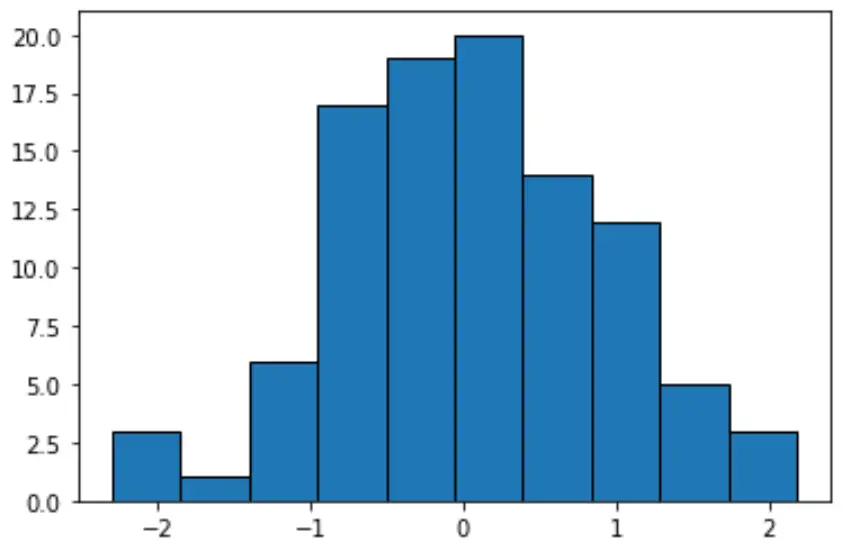
تمتلك كل مجموعة عرضًا متساويًا يبلغ حوالي 0.4487، لكن كل مجموعة لا تحتوي على قدر متساوٍ من الملاحظات. على سبيل المثال:

• يمتد الصندوق الأول من -2.3015387 إلى -1.8528279 ويحتوي على 3 ملاحظات.
• تمتد الحاوية الثانية من -1.8528279 إلى -1.40411588 وتحتوي على ملاحظة واحدة.
• يمتد الصندوق الثالث من -1.40411588 إلى -0.95540447 ويحتوي على 6 ملاحظات.

وما إلى ذلك وهلم جرا.

تجميع التردد المتساوي:

لإنشاء مجموعات تحتوي على عدد متساوٍ من الملاحظات، يمكننا استخدام الدالة التالية:

 #define function to calculate equal-frequency bins 
def equalObs(x, nbin):
    nlen = len(x)
    return np.interp(np.linspace(0, nlen, nbin + 1),
                     np.arange(nlen),
                     np.sort(x))

#create histogram with equal-frequency bins 
n, bins, patches = plt.hist(data, equalObs(data, 10), edgecolor='black')
plt.show()

#display bin boundaries and frequency per bin 
bins, n

(array([-2.3015387 , -0.93576943, -0.67124613, -0.37528495, -0.20889423,
         0.07734007, 0.2344157, 0.51292982, 0.86540763, 1.19891788,
         2.18557541]),
 array([10., 10., 10., 10., 10., 10., 10., 10., 10., 10.])) 

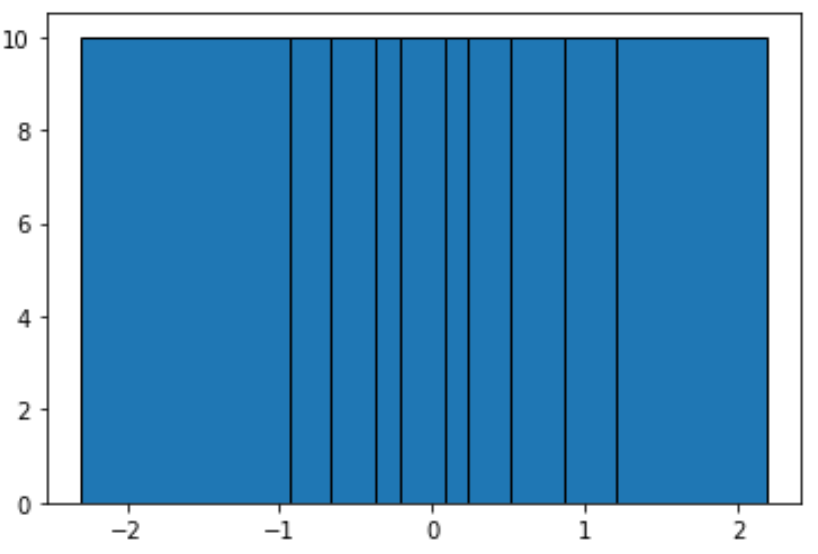
كل مجموعة ليست متساوية في العرض، ولكن كل مجموعة تحتوي على قدر متساو من الملاحظات. على سبيل المثال:

• يمتد الصندوق الأول من -2.3015387 إلى -0.93576943 ويحتوي على 10 ملاحظات.
• يمتد الصندوق الثاني من -0.93576943 إلى -0.67124613 ويحتوي على 10 ملاحظات.
• تمتد الحاوية الثالثة من -0.67124613 إلى -0.37528495 وتحتوي على 10 ملاحظات.

وما إلى ذلك وهلم جرا.

يمكننا أن نرى من الرسم البياني أنه من الواضح أن كل صندوق ليس بنفس العرض، ولكن كل صندوق يحتوي على نفس عدد الملاحظات، وهو ما تؤكده حقيقة أن ارتفاع كل صندوق متساوٍ.