ما هي مقايضة التحيز والتباين في التعلم الآلي؟

لتقييم أداء نموذج ما على مجموعة بيانات، نحتاج إلى قياس مدى تطابق تنبؤات النموذج مع البيانات المرصودة.

بالنسبة لنماذج الانحدار ، المقياس الأكثر استخدامًا هو متوسط مربع الخطأ (MSE)، والذي يتم حسابه على النحو التالي:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

ذهب:

• ن : العدد الإجمالي للملاحظات
• y _i : قيمة الاستجابة للملاحظة ^رقم
• f( _xi ): قيمة الاستجابة المتوقعة ^{للملاحظة} i

كلما كانت تنبؤات النموذج أقرب إلى الملاحظات، كلما انخفض MSE.

ومع ذلك، فإننا نهتم فقط باختبار MSE – MSE عندما يتم تطبيق نموذجنا على البيانات غير المرئية. وذلك لأننا نهتم فقط بكيفية أداء النموذج على البيانات غير المعروفة، وليس على البيانات الموجودة.

على سبيل المثال، من الجيد أن يكون النموذج الذي يتنبأ بأسعار الأسهم منخفضًا في البيانات التاريخية، لكننا نريد حقًا أن نكون قادرين على استخدام النموذج للتنبؤ بالبيانات المستقبلية بدقة.

اتضح أنه لا يزال من الممكن تقسيم اختبار MSE إلى قسمين:

(1) التباين: يشير إلى المقدار الذي ستتغير فيه وظيفتنا f إذا قمنا بتقديرها باستخدام مجموعة تدريب مختلفة.

(2) الانحياز: يشير إلى الخطأ الناتج عن التعامل مع مشكلة حقيقية، والتي قد تكون معقدة للغاية، باستخدام نموذج أبسط بكثير.

مكتوبة من الناحية الرياضية:

اختبار MSE = Var( f̂( x ₀ ) ) + [التحيز( f̂( x ₀ )))] ² + Var(ε)

اختبار MSE = التباين + الانحياز ² + خطأ غير قابل للاختزال

المصطلح الثالث، الخطأ غير القابل للاختزال، هو الخطأ الذي لا يمكن اختزاله بأي نموذج لمجرد وجود ضجيج دائمًا في العلاقة بين مجموعة المتغيرات التفسيرية ومتغير الاستجابة .

النماذج ذات الانحياز العالي تميل إلى أن تكون ذات تباين منخفض . على سبيل المثال، تميل نماذج الانحدار الخطي إلى الانحياز العالي (بافتراض وجود علاقة خطية بسيطة بين المتغيرات التوضيحية ومتغير الاستجابة) والتباين المنخفض (لن تتغير تقديرات النموذج كثيرًا من عينة إلى أخرى). الأخرى).

ومع ذلك، تميل النماذج ذات الانحياز المنخفض إلى الحصول على تباين عالٍ . على سبيل المثال، تميل النماذج غير الخطية المعقدة إلى أن تكون ذات انحياز منخفض (لا تفترض وجود علاقة معينة بين المتغيرات التوضيحية ومتغير الاستجابة) مع تباين عالٍ (يمكن أن تتغير تقديرات النموذج بشكل كبير من عينة تعلم إلى أخرى).

مقايضة التحيز والتباين

تشير مقايضة التحيز والتباين إلى المقايضة التي تحدث عندما نختار تقليل التحيز، مما يؤدي بشكل عام إلى زيادة التباين، أو تقليل التباين، مما يؤدي بشكل عام إلى زيادة التحيز.

يقدم الرسم البياني التالي طريقة لتصور هذه المقايضة:

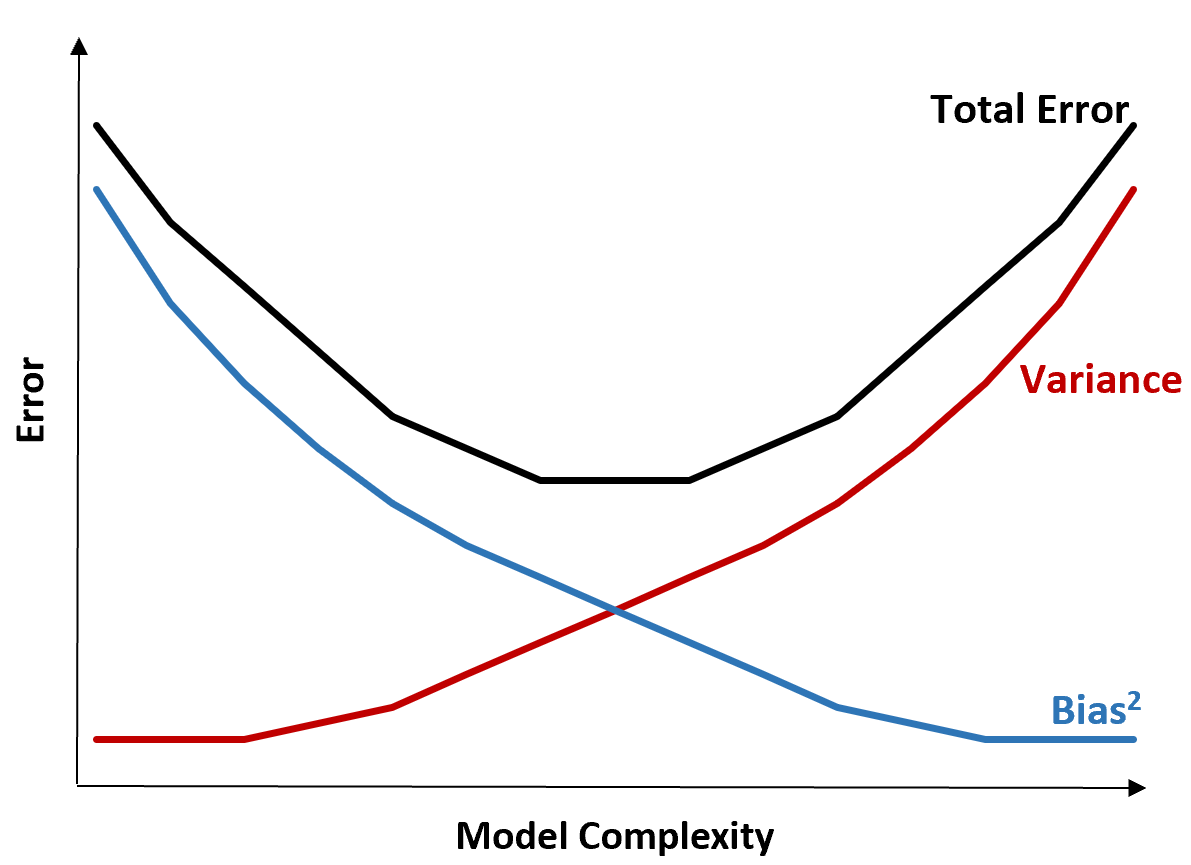
يتناقص إجمالي الخطأ مع زيادة تعقيد النموذج، ولكن حتى نقطة معينة فقط. وبعد نقطة معينة، يبدأ التباين في الزيادة ويبدأ الخطأ الإجمالي أيضًا في الزيادة.

من الناحية العملية، نحن نهتم فقط بتقليل الخطأ الإجمالي للنموذج، وليس بالضرورة تقليل التباين أو التحيز. لقد اتضح أن الطريقة لتقليل الخطأ الإجمالي هي إيجاد التوازن الصحيح بين التباين والتحيز.

بمعنى آخر، نريد نموذجًا معقدًا بدرجة كافية لالتقاط العلاقة الحقيقية بين المتغيرات التوضيحية ومتغير الاستجابة، ولكن ليس معقدًا جدًا لاكتشاف الأنماط غير الموجودة بالفعل.

عندما يكون النموذج معقدًا جدًا، فإنه يفرط في البيانات. يحدث هذا لأنه من الصعب جدًا العثور على أنماط في بيانات التدريب ناتجة عن الصدفة. من المرجح أن يكون أداء هذا النوع من النماذج ضعيفًا عند استخدام البيانات غير المرئية.

ولكن عندما يكون النموذج بسيطًا للغاية، فإنه يقلل من أهمية البيانات. يحدث هذا لأنه من المفترض أن العلاقة الحقيقية بين المتغيرات التوضيحية ومتغير الاستجابة أبسط مما هي عليه في الواقع.

تتمثل طريقة اختيار النماذج المثالية في التعلم الآلي في إيجاد توازن بين التحيز والتباين لتقليل خطأ اختبار النموذج على البيانات غير المرئية المستقبلية.

من الناحية العملية، الطريقة الأكثر شيوعًا لتقليل MSE للاختبارات هي استخدام التحقق المتقاطع .