شرح مبسط لتصحيح الاستمرارية في الإحصاء
يتم تطبيق تصحيح الاستمرارية عندما تريد استخدام التوزيع المستمر لتقريب التوزيع المنفصل. بشكل عام، يتم استخدامه عندما تريد استخدامالتوزيع الطبيعي لتقريب التوزيع ذي الحدين .
تذكر أن التوزيع ذو الحدين يخبرنا باحتمال تحقيق نجاح x في تجارب n ، نظرًا لأن احتمال النجاح في تجربة واحدة هو p . للإجابة على أسئلة حول الاحتمالية مع التوزيع ذي الحدين، يمكننا ببساطة استخدام حاسبة التوزيع ذات الحدين ، ولكن يمكننا أيضًا تقريب الاحتمالية باستخدام التوزيع الطبيعي مع تصحيح الاستمرارية.
تصحيح الاستمرارية هو الاسم الذي يطلق على إضافة أو طرح 0.5 من قيمة x منفصلة .
على سبيل المثال، لنفترض أننا نريد إيجاد احتمال سقوط العملة على الصور أقل من أو تساوي 45 مرة على مدار 100 رمية. أي أننا نريد إيجاد P(X ≥ 45). لاستخدام التوزيع الطبيعي لتقريب التوزيع ذي الحدين، سنجد بدلاً من ذلك P(X ≥ 45.5).
يوضح الجدول التالي متى يجب عليك إضافة أو طرح 0.5، اعتمادًا على نوع الاحتمال الذي تحاول العثور عليه:
| استخدم التوزيع ذي الحدين | استخدام التوزيع الطبيعي مع تصحيح الاستمرارية |
|---|---|
| س = 45 | 44.5 < س < 45.5 |
| × ≥ 45 | س <45.5 |
| × < 45 | س <44.5 |
| × ≥ 45 | س > 44.5 |
| ×> 45 | × > 45.5 |
ملحوظة:
من المناسب فقط تطبيق تصحيح الاستمرارية على التوزيع الطبيعي لتقريب التوزيع ذي الحدين عندما يكون كل من n*p وn*(1-p) على الأقل 5.
على سبيل المثال، لنفترض أن n = 15 وp = 0.6. في هذه الحالة:
ن*ع = 15 * 0.6 = 9
ن*(1-ع) = 15 * (1 – 0.6) = 15 * (0.4) = 6
وبما أن هذين الرقمين أكبر من أو يساوي 5، فسيكون من المقبول تطبيق تصحيح الاستمرارية في هذا السيناريو.
يوضح المثال التالي كيفية تطبيق تصحيح الاستمرارية على التوزيع الطبيعي لتقريب التوزيع ذي الحدين.
مثال على تطبيق تصحيح الاستمرارية
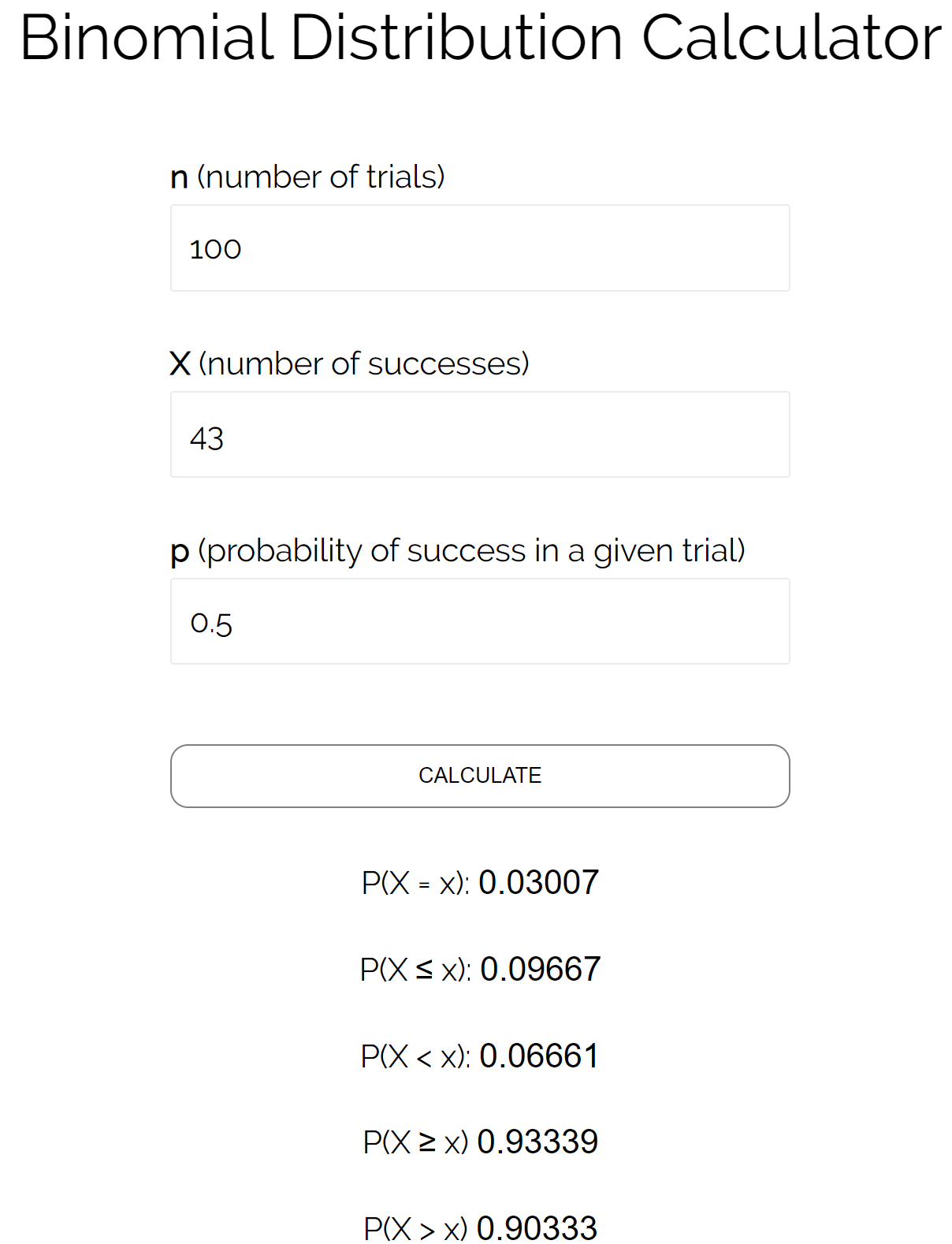
لنفترض أننا نريد معرفة احتمال سقوط العملة على رؤوس أقل من أو تساوي 43 مرة في 100 رمية. في هذه الحالة:
ن = عدد التجارب = 100
X = عدد النجاحات = 43
ع = احتمال النجاح في تجربة معينة = 0.50
يمكننا إدخال هذه الأرقام في حاسبة التوزيع ذات الحدين لنرى أن احتمال سقوط العملة على رؤوس أقل من أو يساوي 43 مرة هو 0.09667 .
لتقريب التوزيع ذي الحدين من خلال تطبيق تصحيح الاستمرارية على التوزيع الطبيعي، يمكننا استخدام الخطوات التالية:
الخطوة 1: تحقق من أن n*p و n*(1-p) كلاهما على الأقل 5 .
ن*ع = 100*0.5 = 50
ن*(1-ع) = 100*(1 – 0.5) = 100*0.5 = 50
كلا الرقمين أكبر من أو يساوي 5، حتى نتمكن من الاستمرار.
الخطوة 2: تحديد ما إذا كنت تريد إضافة أو طرح 0.5
وبالرجوع إلى الجدول أعلاه نرى أنه من المفترض أن نضيف 0.5 عندما نعمل مع الاحتمالية على شكل X ≥ 43. وبالتالي سنجد P(X< 43.5).
الخطوة 3: ابحث عن المتوسط (μ) والانحراف المعياري (σ) للتوزيع ذي الحدين.
μ = ن*ع = 100*0.5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
الخطوة 4: ابحث عن درجة z باستخدام المتوسط والانحراف المعياري الموجود في الخطوة السابقة.
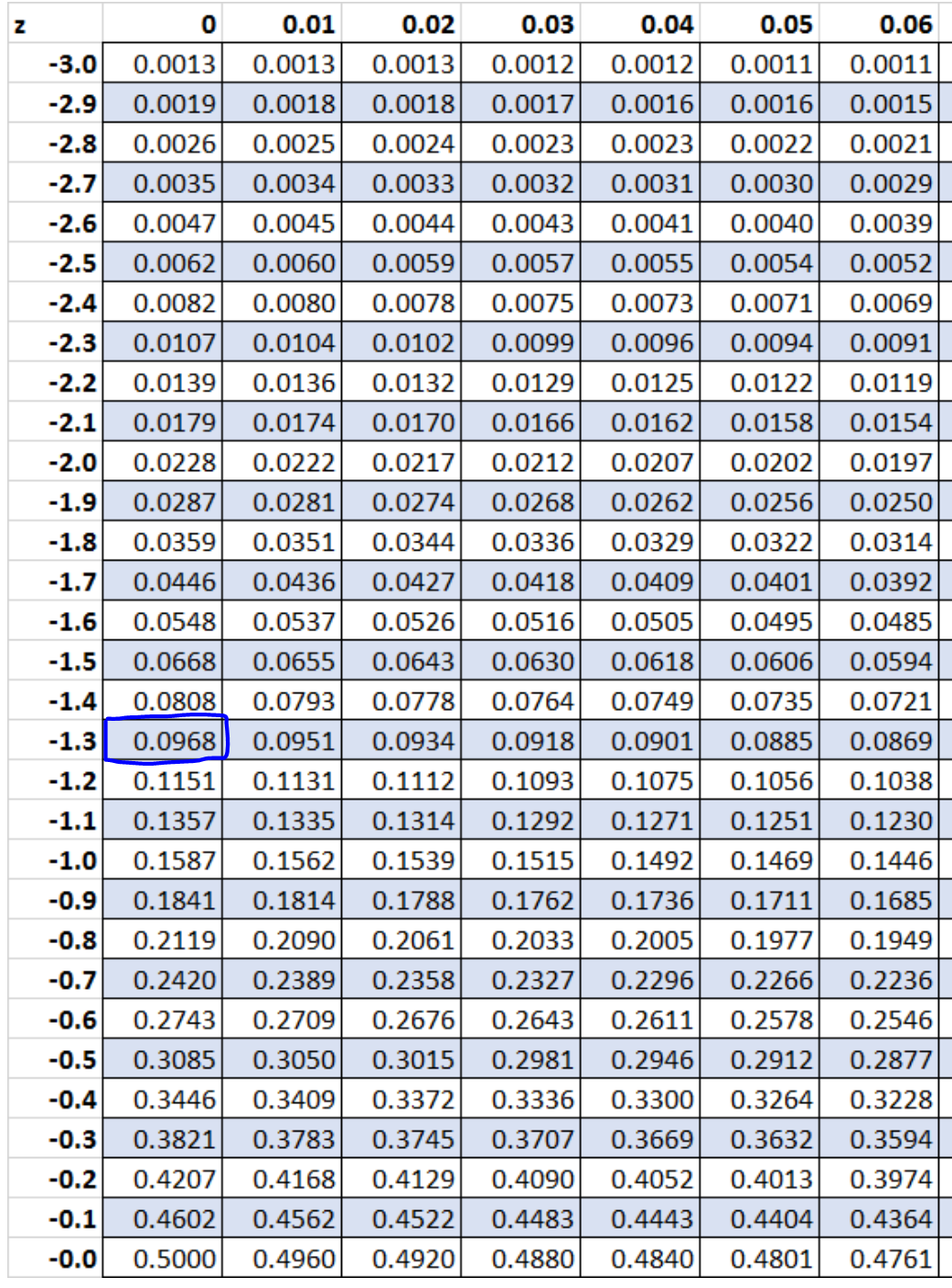
ض = (س – μ) / σ = (43.5 – 50) / 5 = -6.5 / 5 = -1.3.
الخطوة 5: استخدم الجدول Z للعثور على الاحتمالية المرتبطة بدرجة z.
وفقًا للجدول Z، فإن الاحتمال المرتبط بـ z = -1.3 هو 0.0968 .
لذا فإن الاحتمال الدقيق الذي وجدناه باستخدام التوزيع ذي الحدين هو 0.09667 بينما الاحتمال التقريبي الذي وجدناه باستخدام تصحيح الاستمرارية مع التوزيع الطبيعي هو 0.0968 . هاتان القيمتان مغلقتان تمامًا.
متى يتم استخدام تصحيح الاستمرارية
قبل وجود البرامج الإحصائية الحديثة وكان لا بد من إجراء الحسابات يدويًا، كانت تصحيحات الاستمرارية تستخدم في كثير من الأحيان للعثور على الاحتمالات التي تنطوي على توزيعات منفصلة. اليوم، تلعب تصحيحات الاستمرارية دورًا أقل في حساب الاحتمالات حيث يمكننا عادةً الاعتماد على البرامج أو الآلات الحاسبة لحساب الاحتمالات بالنسبة لنا.
بدلاً من ذلك، فهو ببساطة موضوع يتم تناوله في دورات الإحصاء لتوضيح العلاقة بين التوزيع ذي الحدين والتوزيع الطبيعي وإظهار أنه من الممكن للتوزيع الطبيعي أن يقترب من التوزيع ذي الحدين من خلال تطبيق تصحيح الاستمرارية.
حاسبة تصحيح الاستمرارية
استخدم حاسبة تصحيح الاستمرارية لتطبيق تصحيح الاستمرارية تلقائيًا على التوزيع الطبيعي لتقريب الاحتمالات ذات الحدين.