كيفية تطبيع البيانات في إكسيل

“تطبيع” مجموعة من قيم البيانات يعني قياس القيم بحيث يكون متوسط جميع القيم 0 والانحراف المعياري هو 1.

يشرح هذا البرنامج التعليمي كيفية تسوية البيانات في Excel.

مثال: كيفية تطبيع البيانات في Excel

لنفترض أن لدينا مجموعة البيانات التالية في Excel:

أكمل الخطوات التالية لتطبيع هذه المجموعة من قيم البيانات.

الخطوة 1: العثور على المتوسط.

أولاً، سوف نستخدم الدالة =AVERAGE(نطاق القيم) للعثور على متوسط مجموعة البيانات.

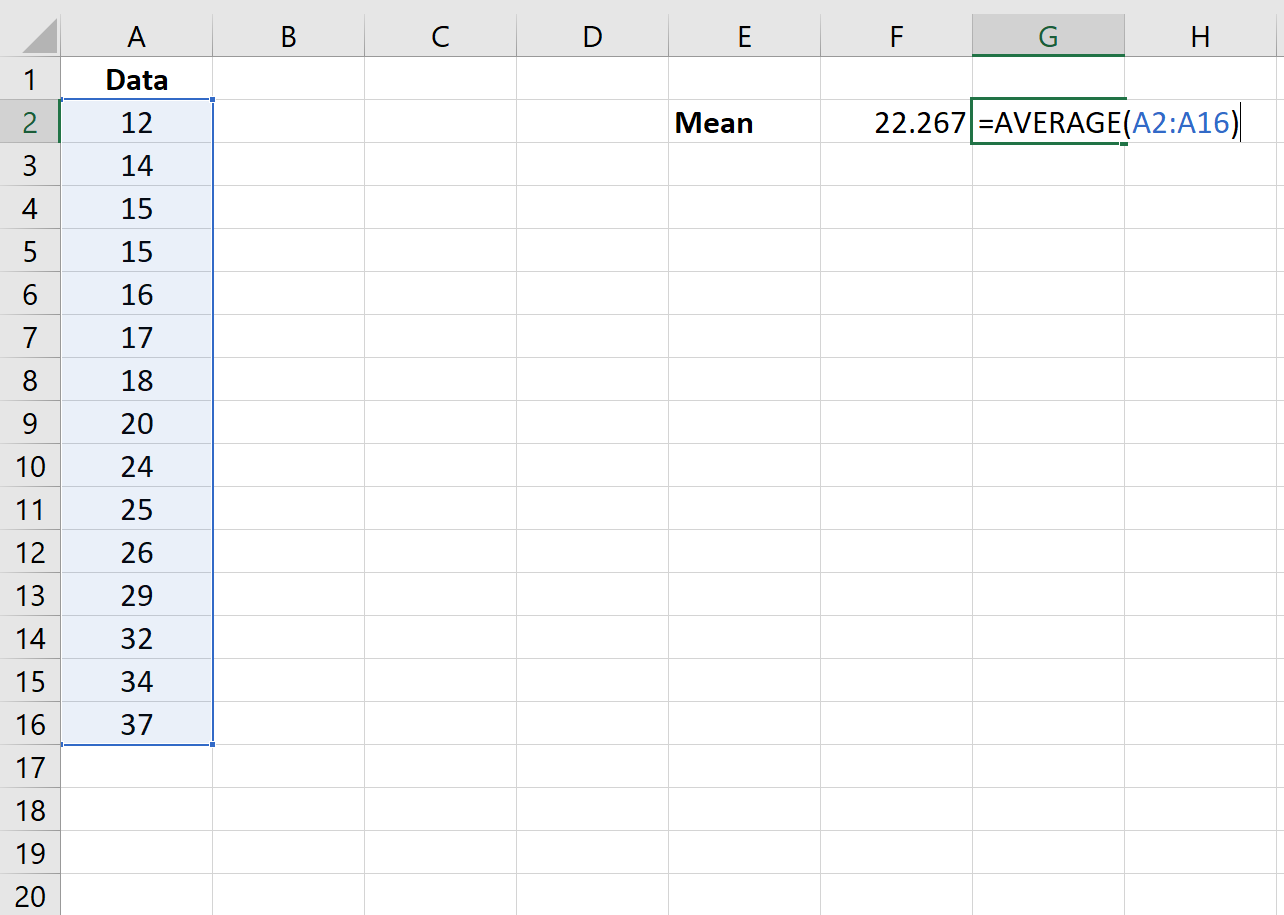
الخطوة 2: العثور على الانحراف المعياري.

بعد ذلك، سوف نستخدم الدالة = STDEV (نطاق القيم) للعثور على الانحراف المعياري لمجموعة البيانات.

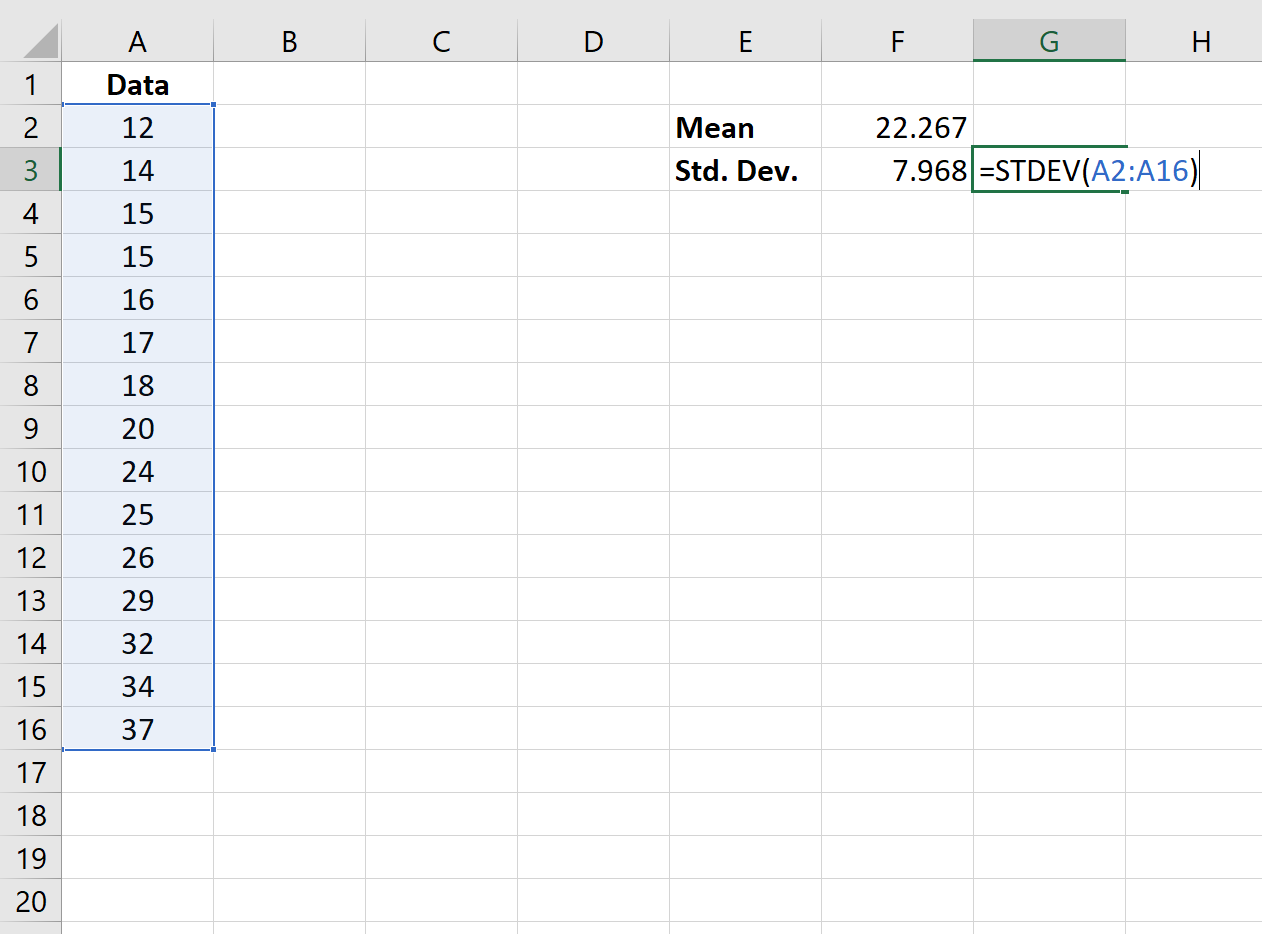
الخطوة 3: تطبيع القيم.

أخيرًا، سنستخدم الدالة STANDARDIZE(x, Mean, Standard_dev) لتطبيع كل قيمة من القيم في مجموعة البيانات.

ملحوظة:

تستخدم الدالة STANDARDIZE الصيغة التالية لتطبيع قيمة بيانات معينة:

القيمة المقيسة = (x – x ) / s

ذهب:

• س = قيمة البيانات
• x = متوسط مجموعة البيانات
• s = الانحراف المعياري لمجموعة البيانات

توضح الصورة التالية الصيغة المستخدمة لتطبيع القيمة الأولى في مجموعة البيانات:

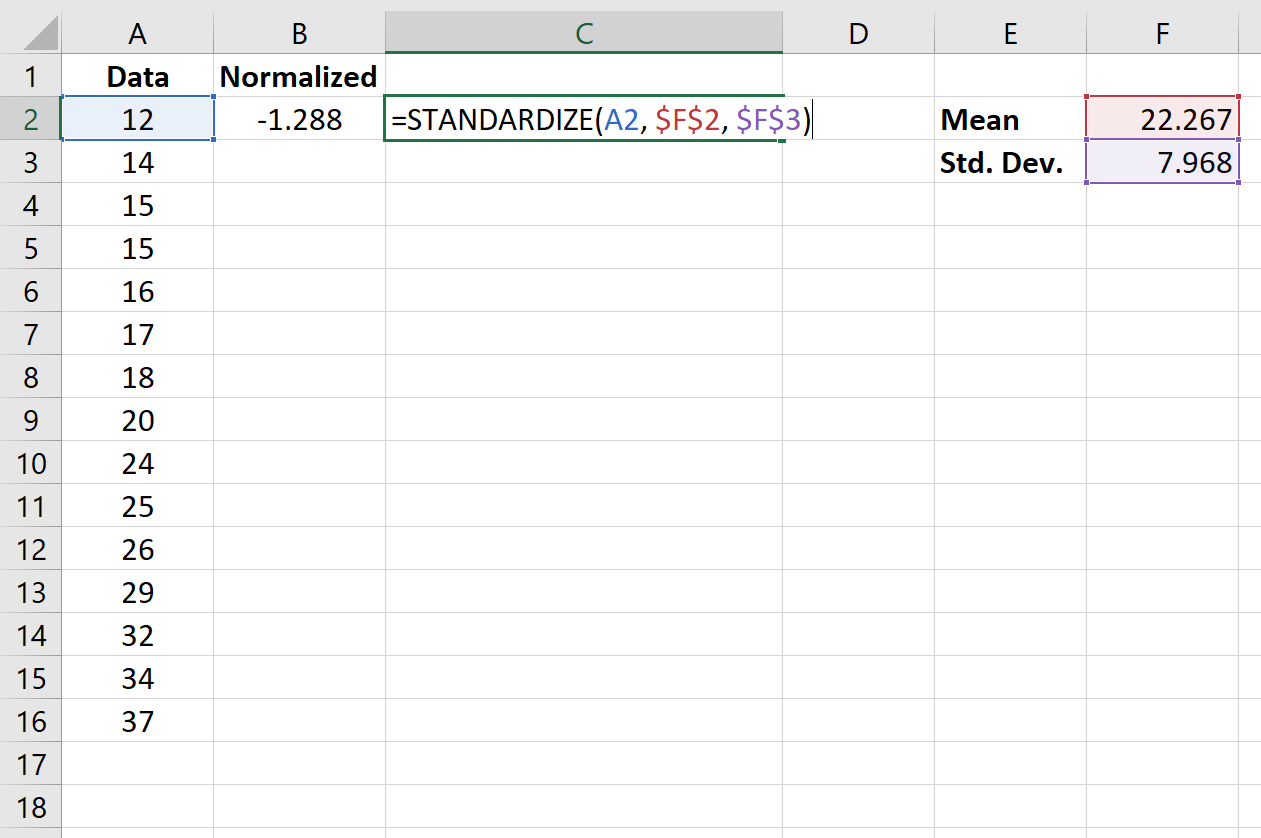
بمجرد تسوية القيمة الأولى في الخلية B2، يمكننا المرور فوق الركن الأيمن السفلي من الخلية B2 حتى تظهر علامة + صغيرة. انقر نقرًا مزدوجًا فوق + لنسخ الصيغة إلى الخلايا المتبقية:

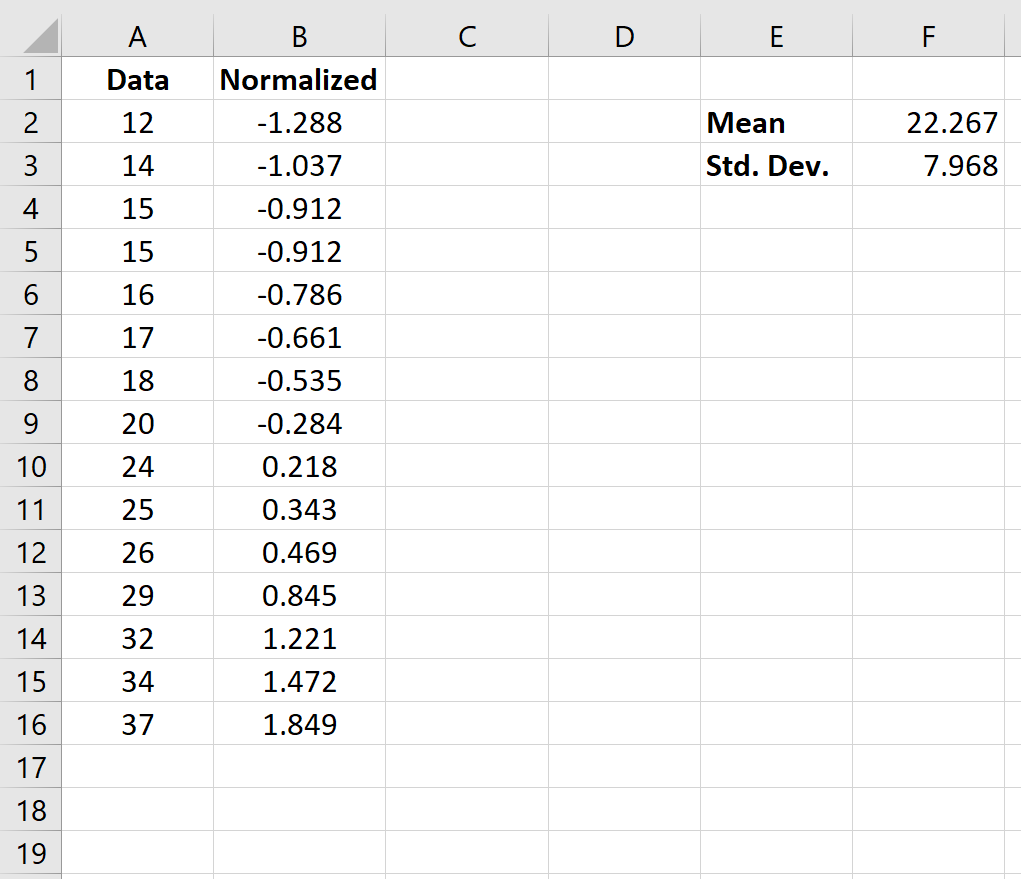
الآن تمت تسوية كل قيمة في مجموعة البيانات.

كيفية تفسير البيانات المقيسة

الصيغة التي استخدمناها لتطبيع قيمة بيانات معينة، x، كانت:

القيمة المقيسة = (x – x ) / s

ذهب:

• س = قيمة البيانات
• x = متوسط مجموعة البيانات
• s = الانحراف المعياري لمجموعة البيانات

إذا كانت نقطة بيانات معينة لها قيمة طبيعية أكبر من 0، فهذا يشير إلى أن نقطة البيانات أعلى من المتوسط. وعلى العكس من ذلك، تشير القيمة المقيسة الأقل من 0 إلى أن نقطة البيانات أقل من المتوسط.

على وجه الخصوص، تخبرنا القيمة المقيسة بعدد الانحرافات المعيارية التي تمثلها نقطة البيانات الأصلية عن المتوسط. على سبيل المثال، ضع في اعتبارك نقطة البيانات “12” في مجموعة البيانات الأصلية لدينا:

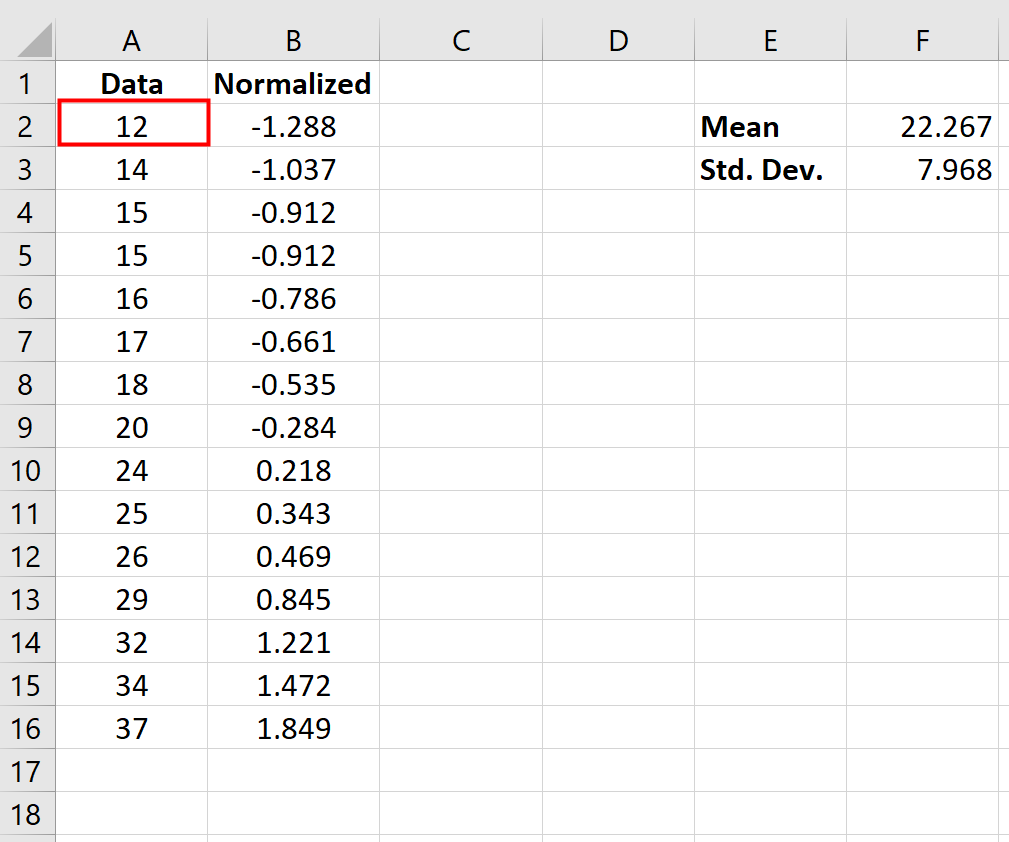
وتبين أن القيمة الطبيعية لـ “12” هي -1.288، ويتم حسابها على النحو التالي:

القيمة الطبيعية = (x – x ) / s = (12 – 22.267) / 7.968 = -1.288

يخبرنا هذا أن القيمة “12” أقل بمقدار 1.288 انحرافًا معياريًا عن متوسط مجموعة البيانات الأصلية.

يمكن أن تساعدنا كل من القيم المقيسة في مجموعة البيانات في فهم مدى قرب أو بعد قيمة بيانات معينة عن المتوسط. تشير القيمة المقيسة الصغيرة إلى أن القيمة قريبة من المتوسط بينما تشير القيمة المقيسة الكبيرة إلى أن القيمة بعيدة عن المتوسط.