تركيب المنحنى في برنامج excel (مع أمثلة)

قد ترغب في كثير من الأحيان في العثور على المعادلة التي تناسب المنحنى بشكل أفضل لمجموعة من البيانات في Excel.

ولحسن الحظ، يعد القيام بذلك أمرًا بسيطًا للغاية باستخدام وظيفة خط الاتجاه في Excel.

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية ملاءمة معادلة لمنحنى في Excel.

الخطوة 1: إنشاء البيانات

أولاً، لنقم بإنشاء مجموعة بيانات مزيفة للعمل معها:

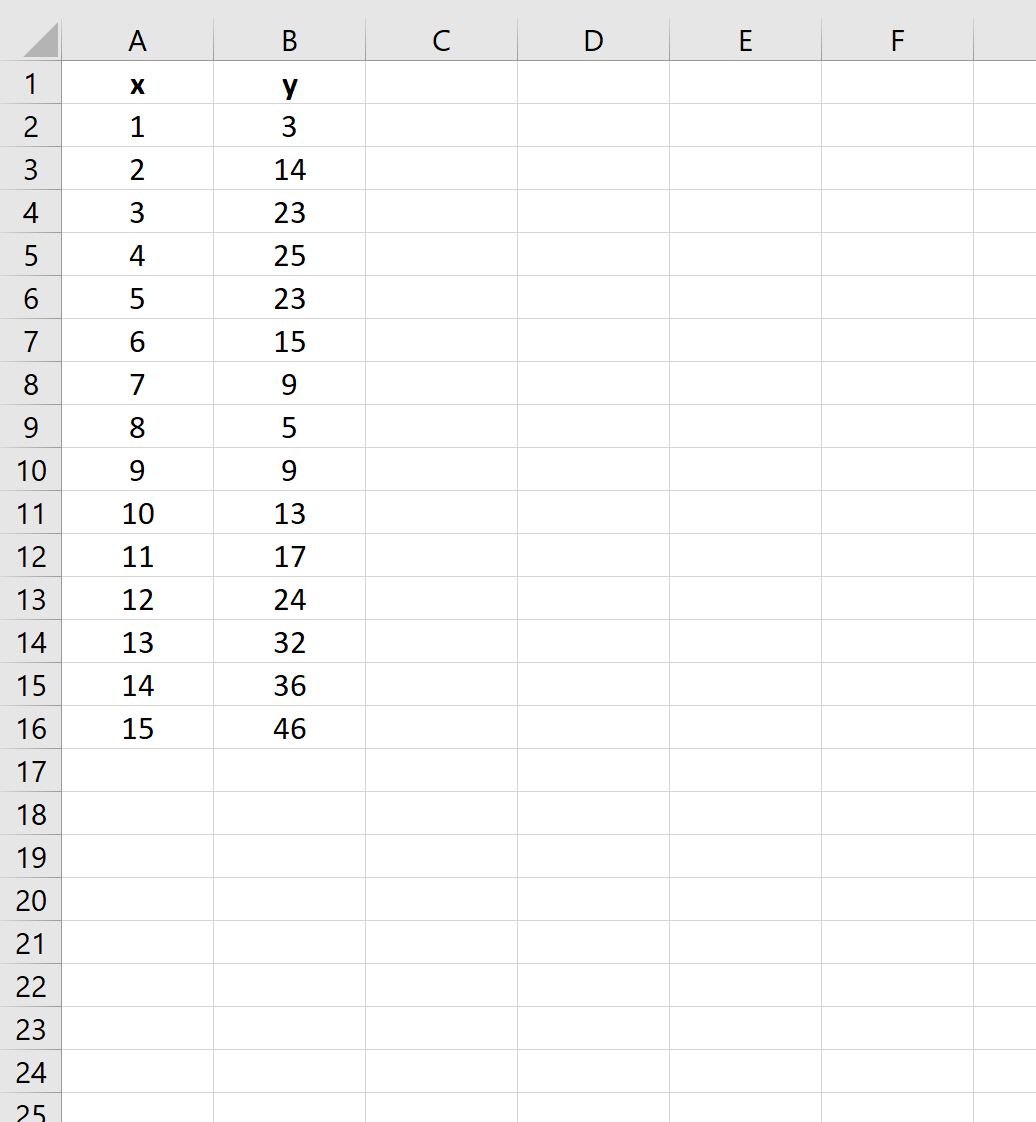
الخطوة 2: إنشاء مخطط مبعثر

بعد ذلك، دعونا ننشئ مخططًا مبعثرًا لتصور مجموعة البيانات.

أولاً، قم بتمييز الخلايا A2:B16 كما يلي:

بعد ذلك، انقر فوق علامة التبويب “إدراج” على طول الشريط العلوي، ثم انقر فوق خيار الرسم الأول ضمن “Scatter” :

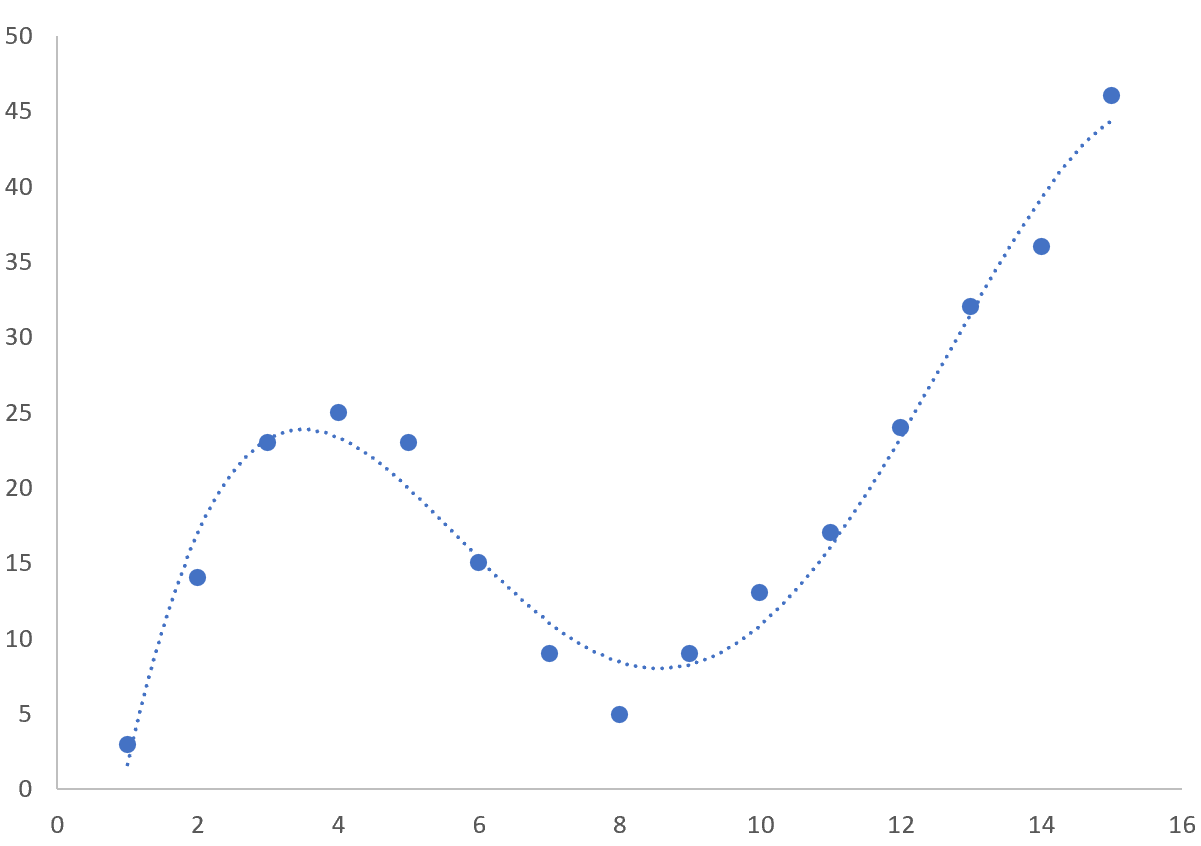
وينتج عن ذلك المخطط المبعثر التالي:

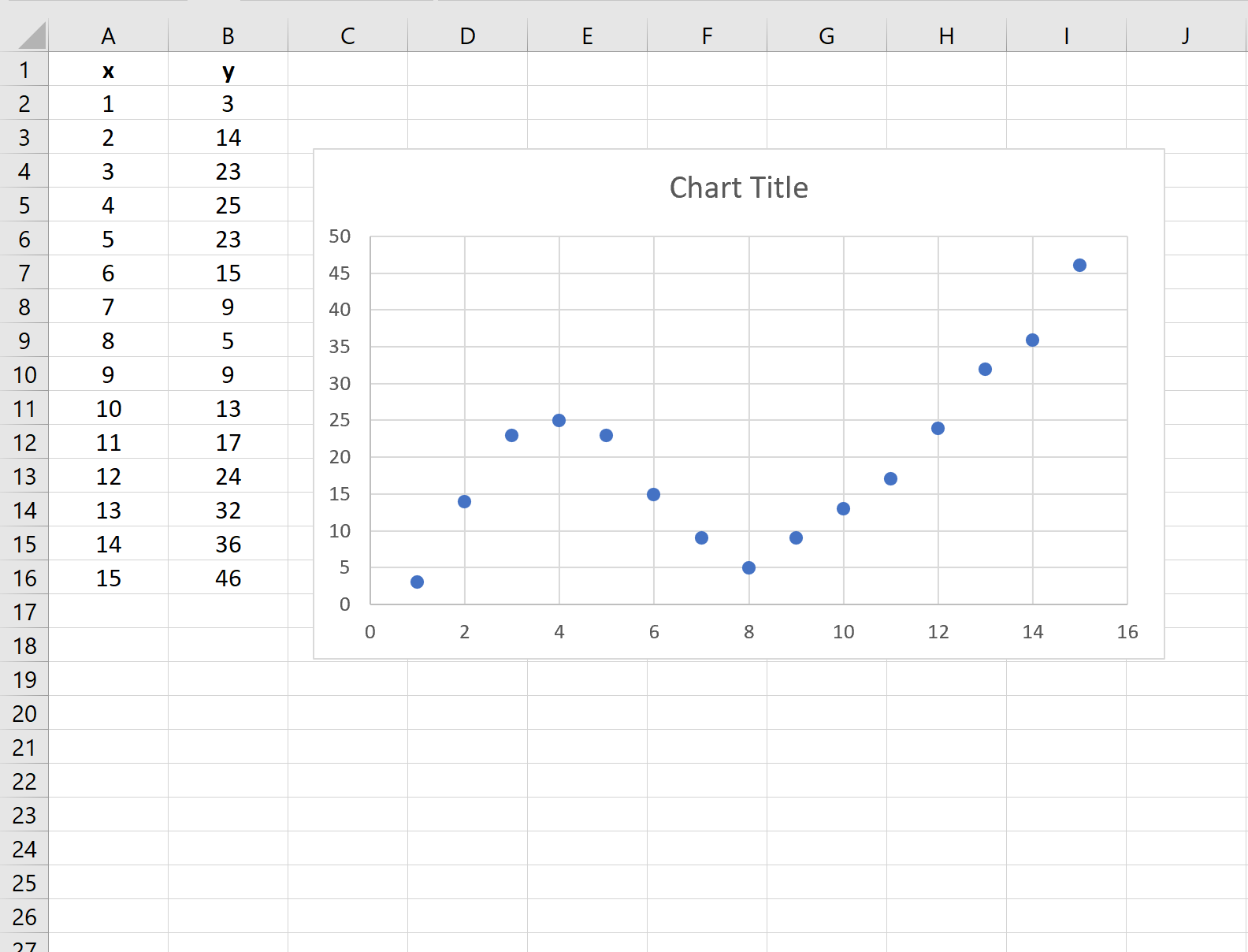
الخطوة 3: إضافة خط الاتجاه

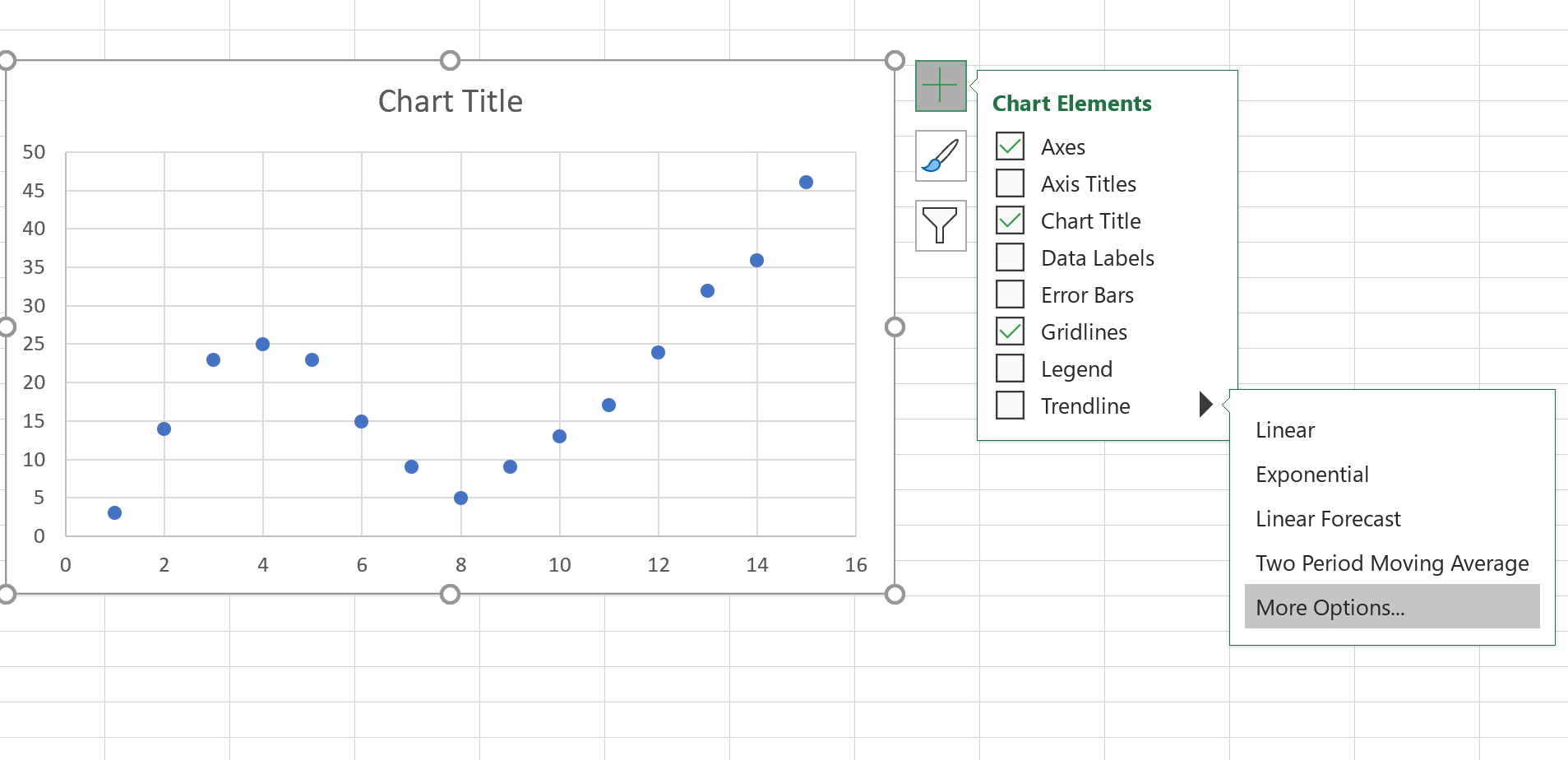
بعد ذلك، انقر في أي مكان على مخطط التشتت. ثم انقر على علامة + في الزاوية اليمنى العليا. في القائمة المنسدلة، انقر فوق السهم الموجود بجوار خط الاتجاه ، ثم انقر فوق المزيد من الخيارات :

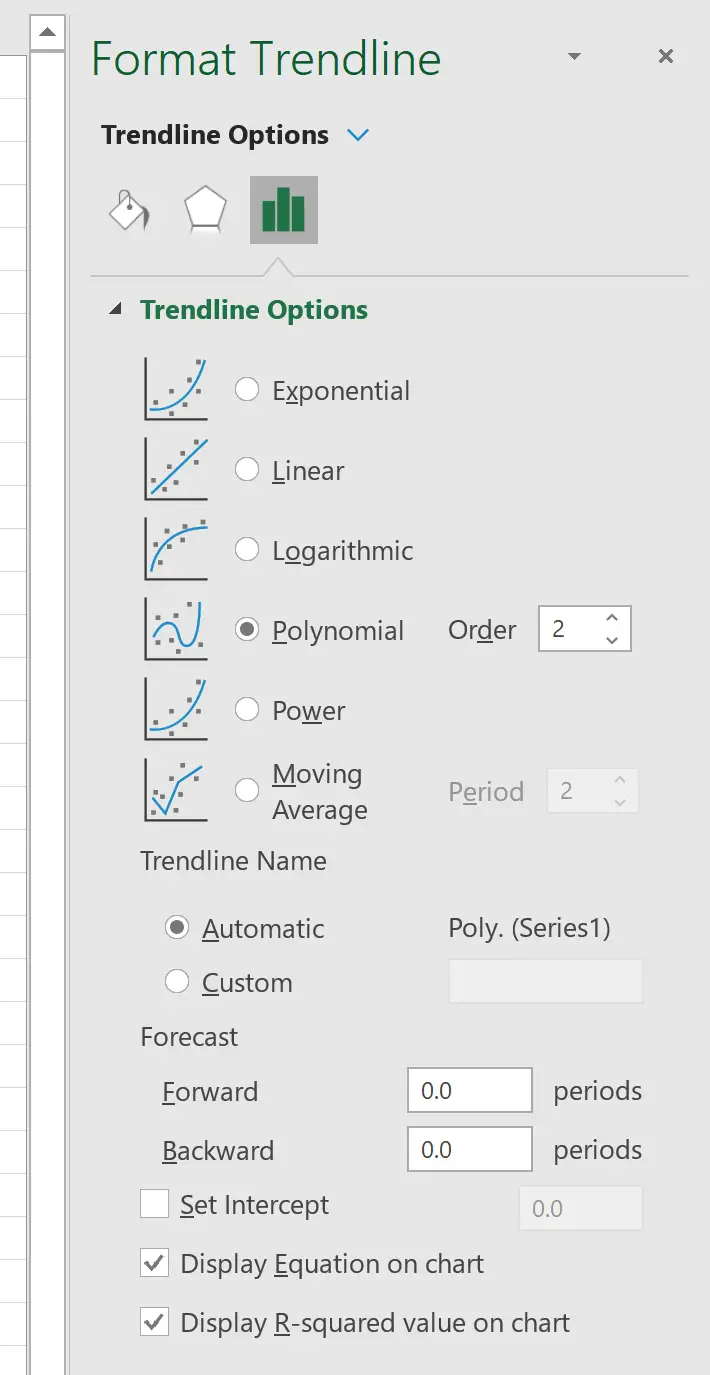
في النافذة التي تظهر على اليمين، انقر فوق الزر الموجود بجوار متعدد الحدود . ثم حدد المربعين بجوار إظهار المعادلة على الرسم البياني وإظهار قيمة R-squared على الرسم البياني .

ينتج عن هذا المنحنى التالي على السحابة النقطية:

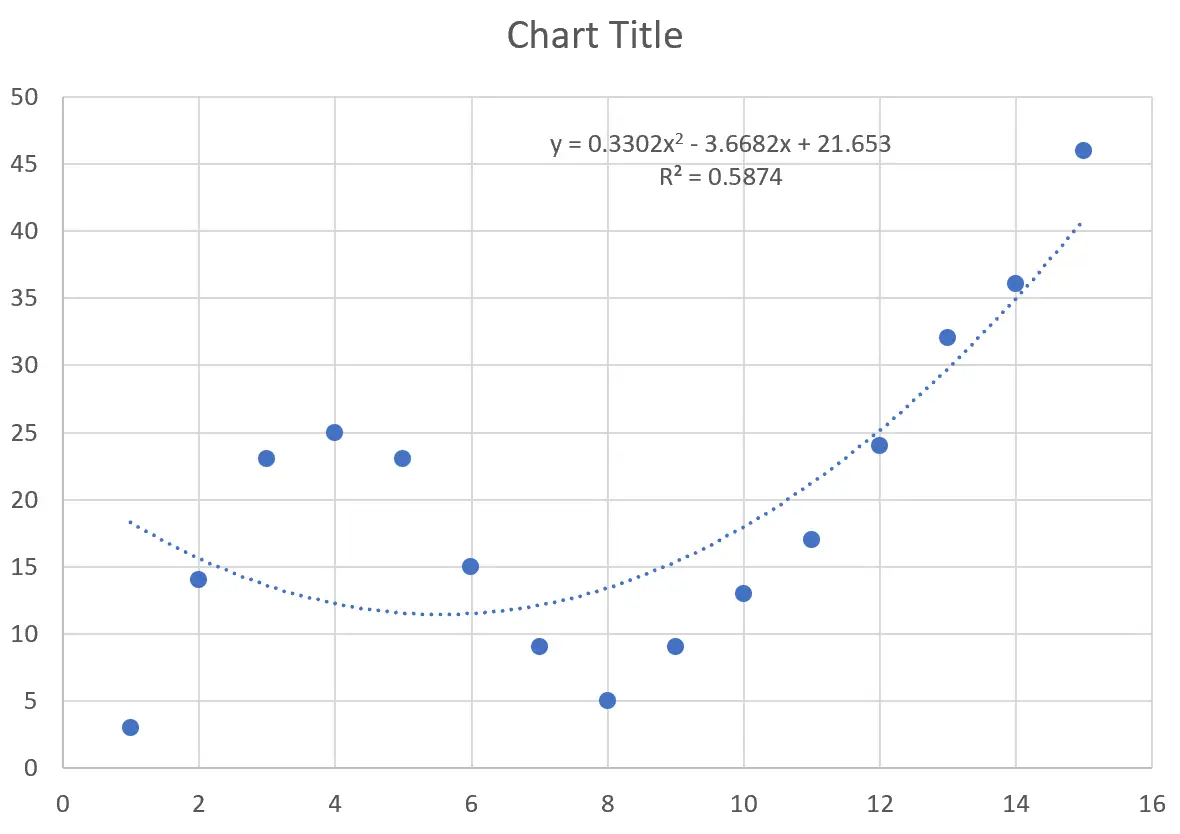
معادلة المنحنى هي كما يلي:

ص = 0.3302س ² – 3.6682س + 21.653

يخبرنا R-squared النسبة المئوية للتباين في متغير الاستجابة الذي يمكن تفسيره بواسطة المتغيرات المتوقعة. مربع R لهذا المنحنى بالذات هو 0.5874 .

الخطوة 4: اختر أفضل خط اتجاه

يمكننا أيضًا زيادة ترتيب كثير الحدود الذي نستخدمه لمعرفة ما إذا كان المنحنى الأكثر مرونة يوفر ملاءمة أفضل لمجموعة البيانات.

على سبيل المثال، يمكننا اختيار ضبط ترتيب كثيرات الحدود على 4:

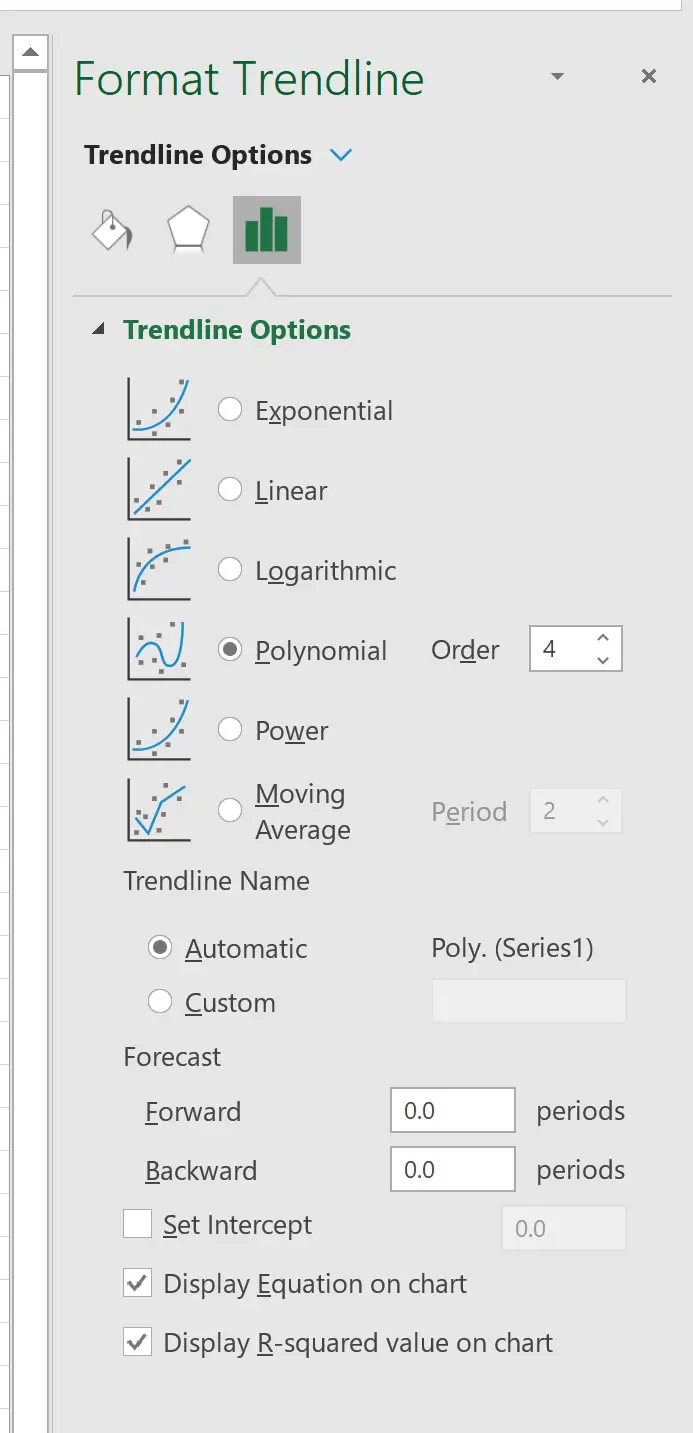
وينتج عن ذلك المنحنى التالي:

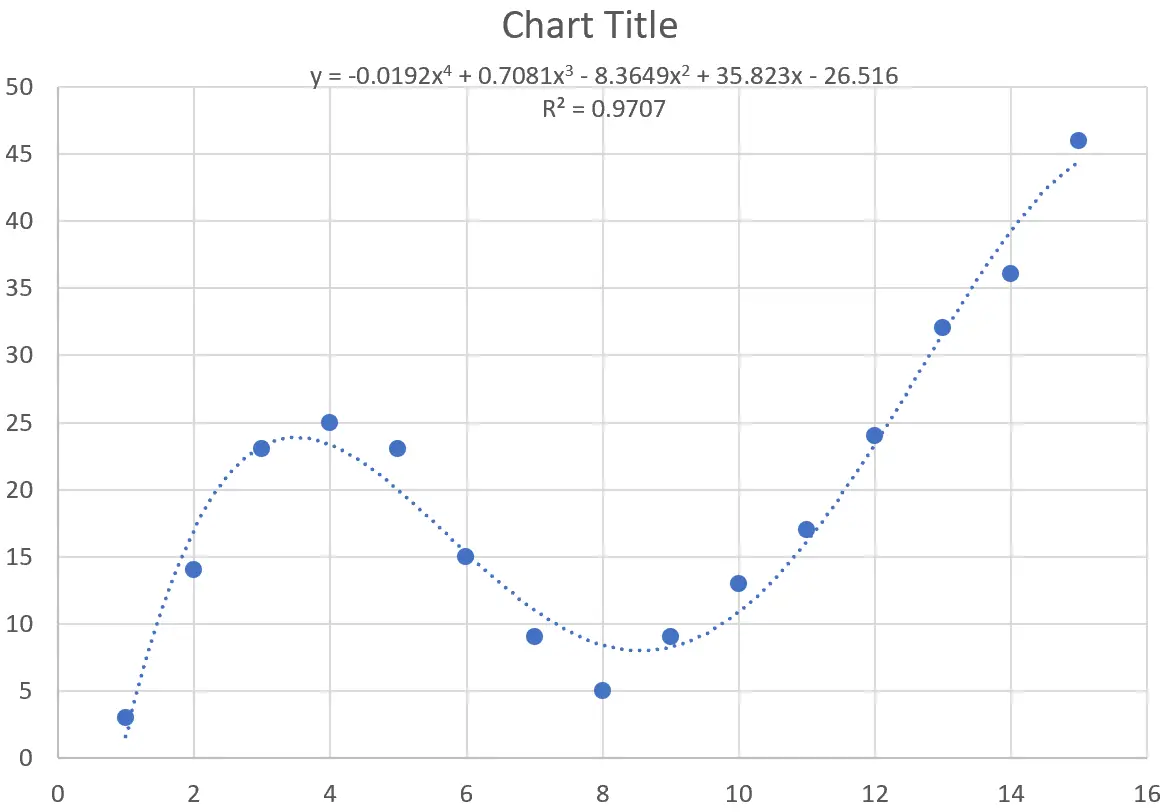
معادلة المنحنى هي كما يلي:

ص = ^-0.0192×4 + ^0.7081×3 – ^8.3649×2 + 35.823x – 26.516

مربع R لهذا المنحنى بالذات هو 0.9707 .

يعتبر مربع R هذا أعلى بكثير من المنحنى السابق، مما يشير إلى أنه يطابق مجموعة البيانات بشكل أوثق.

يمكننا أيضًا استخدام معادلة المنحنى هذه للتنبؤ بقيمة متغير الاستجابة بناءً على متغير التوقع. على سبيل المثال، إذا كانت x = 4 فإننا نتوقع أن y = 23.34 :

ص = -0.0192(4) ⁴ + 0.7081(4) ³ – 8.3649(4) ² + 35.823(4) – 26.516 = 23.34

يمكنك العثور على المزيد من دروس Excel على هذه الصفحة .