الدليل الكامل: كيفية تفسير نتائج anova في excel

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

يوفر المثال التالي دليلاً كاملاً حول كيفية تفسير نتائج ANOVA أحادية الاتجاه في Excel.

مثال: كيفية تفسير نتائج ANOVA في Excel

لنفترض أن المعلم يطلب بشكل عشوائي من 30 طالبًا في فصله استخدام إحدى طرق الدراسة الثلاثة للتحضير للامتحان.

توضح لقطة الشاشة التالية درجات الطلاب بناءً على الطريقة التي استخدموها:

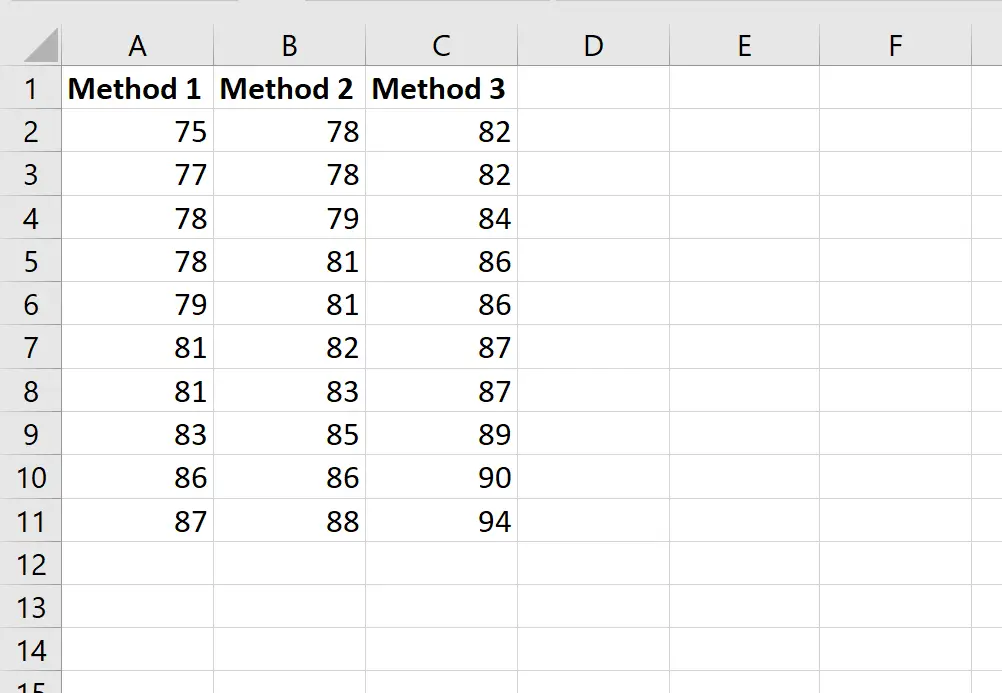
لنفترض أن المعلم يريد إجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كانت الدرجات المتوسطة هي نفسها عبر المجموعات الثلاث.

لإجراء تحليل ANOVA أحادي الاتجاه في Excel، انقر فوق علامة التبويب “بيانات” على طول الشريط العلوي، ثم انقر فوق “تحليل البيانات” في المجموعة “تحليل” .

إذا كنت لا ترى خيار تحليل البيانات ، فيجب عليك أولاً تحميل برنامج Analysis ToolPak المجاني.

بمجرد الضغط عليها، ستظهر نافذة جديدة. حدد Anova: Single Factor ، ثم انقر فوق OK .

في النافذة الجديدة التي تظهر، أدخل المعلومات التالية:

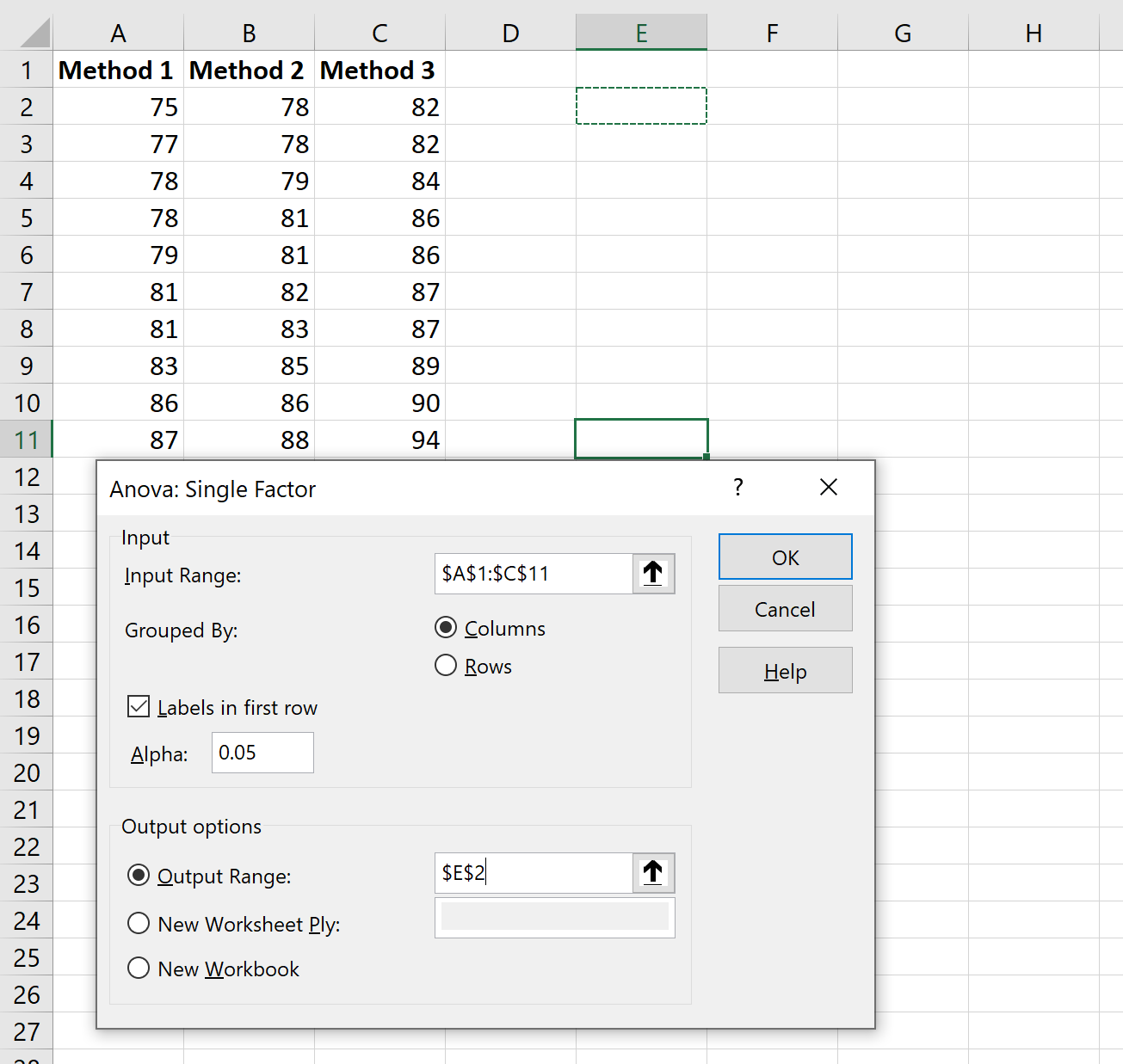
بمجرد النقر فوق “موافق” ، ستظهر نتائج ANOVA أحادية الاتجاه:

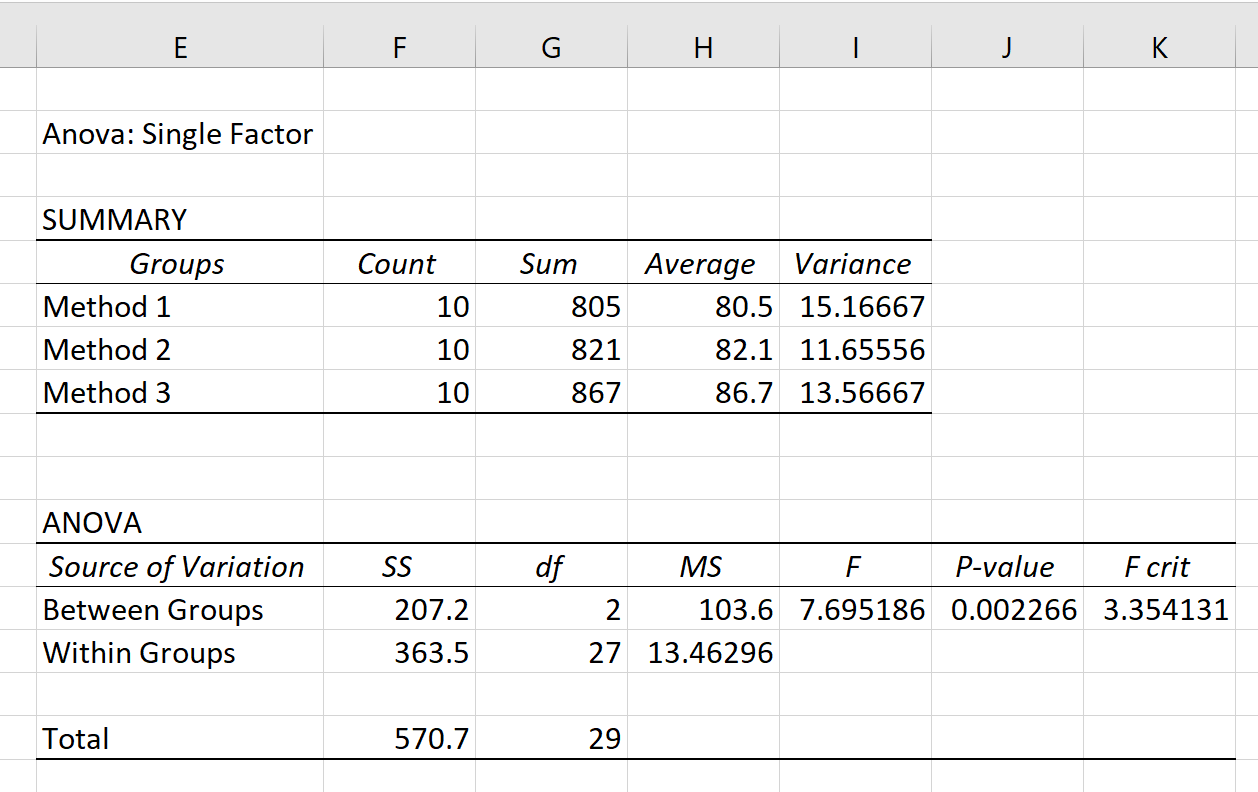
يتم عرض جدولين في النتيجة: SUMMARY و ANOVA .

وإليك كيفية تفسير القيم في كل جدول:

جدول ملخص :

• المجموعات : أسماء المجموعات
• العد : عدد الملاحظات في كل مجموعة
• Sum : مجموع قيم كل مجموعة
• المتوسط : متوسط القيمة في كل مجموعة
• التباين : تباين القيم في كل مجموعة

يوفر لنا هذا الجدول العديد من الإحصائيات الموجزة المفيدة لكل مجموعة مستخدمة في تحليل التباين (ANOVA).

من هذا الجدول يمكننا أن نرى أن الطلاب الذين استخدموا الطريقة الثالثة حصلوا على أعلى متوسط درجات الاختبار (86.7)، ولكن كان لديهم أيضًا أعلى تباين في درجات الاختبار. مراجعة (13.56667).

لتحديد ما إذا كانت الاختلافات في متوسطات المجموعة ذات دلالة إحصائية، يجب علينا الرجوع إلى جدول ANOVA.

جدول تحليل التباين :

• مصدر التباين : التباين المقاس (إما بين المجموعات أو داخل المجموعات)
• SS : مجموع المربعات لكل مصدر من مصادر الاختلاف
• df : درجات الحرية، محسوبة على أنها #groups-1 لـ df بين و #observations – #groups لـ df ضمن
• MS : متوسط مجموع المربعات، محسوبًا بـ SS/df
• F : قيمة F الإجمالية، محسوبة على أنها MS بين / MS في الداخل
• القيمة P : القيمة p المقابلة لقيمة F الإجمالية
• F Crit : القيمة الحرجة F التي تقابل α = 0.05

القيمة الأكثر أهمية في هذا الجدول هي القيمة p ، والتي تبين أنها 0.002266 .

تذكر أن تحليل التباين أحادي الاتجاه يستخدم الفرضيات الصفرية والبديلة التالية:

• H ₀ : جميع وسائل المجموعة متساوية.
• ح _أ : ليست كل متوسطات المجموعة متساوية.

نظرًا لأن القيمة p أقل من α = 0.05، فإننا نرفض الفرضية الصفرية لتحليل التباين أحادي الاتجاه ونستنتج أن لدينا أدلة كافية للإشارة إلى أن جميع وسائل المجموعة غير متساوية.

وهذا يعني أن طرق الدراسة الثلاثة لا تؤدي جميعها إلى نفس متوسط درجات الامتحانات.

ملاحظة : يمكنك أيضًا مقارنة قيمة F الإجمالية بقيمة F الحرجة لتحديد ما إذا كان يجب عليك رفض فرضية العدم أم لا. في هذه الحالة، بما أن القيمة الإجمالية لـ F أكبر من القيمة الحرجة لـ F، فإننا نرفض فرضية العدم. لاحظ أن نهج القيمة p ونهج القيمة F الحرجة سيؤديان دائمًا إلى نفس النتيجة.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء ANOVAs مختلفة في Excel:

كيفية إجراء ANOVA أحادي الاتجاه في Excel
كيفية إجراء ANOVA ثنائي الاتجاه في Excel
كيفية تنفيذ التدابير المتكررة ANOVA في Excel
كيفية إجراء ANOVA المتداخلة في Excel