ما هو تقييد النطاق؟

في كثير من الأحيان نسعى في الإحصائيات إلى قياس العلاقة بين متغيرين. وهذا يساعدنا على فهم ما يلي:

• اتجاه العلاقة بين متغيرين. مع زيادة أحد المتغيرات، هل يميل المتغير الآخر إلى الزيادة أم النقصان؟
• قوة العلاقة بين متغيرين. ما مدى تغير قيمة المتغيرين؟

ولسوء الحظ، فإن المشكلة التي يمكن أن تنشأ عند قياس الارتباط بين متغيرين تسمى تقييد النطاق . يحدث هذا عندما يكون نطاق القيم المقاسة لأحد المتغيرات مقيدًا لسبب ما.

على سبيل المثال، لنفترض أننا نريد قياس الارتباط بين ساعات الدراسة ودرجات امتحانات الطلاب في مدرسة معينة.

إذا قمنا بجمع بيانات عن هذين المتغيرين لجميع الطلاب البالغ عددهم 1000 طالب في المدرسة، فقد نجد أن الارتباط بين ساعات الدراسة ودرجات الامتحانات هو 0.73 .

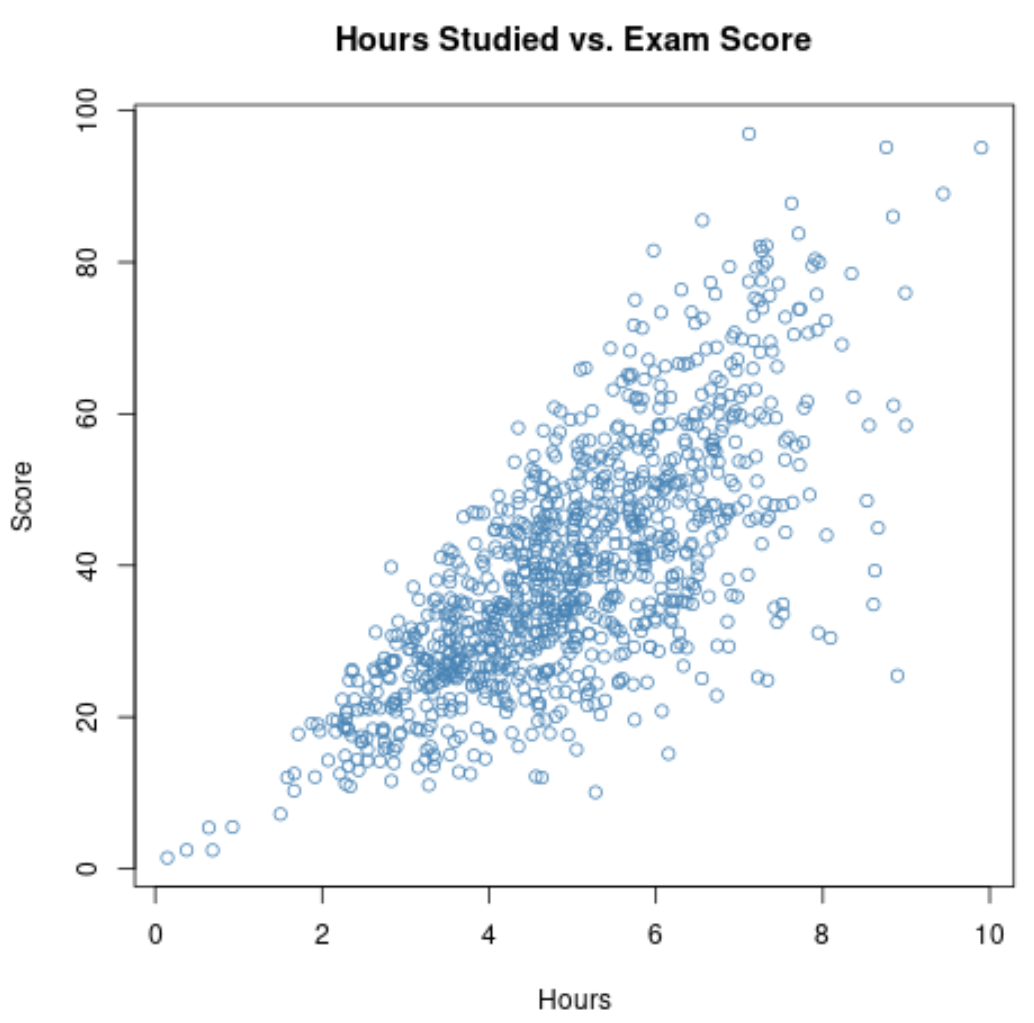
وهذا الارتباط مرتفع جداً مما يدل على وجود علاقة إيجابية قوية بين المتغيرين. عندما يدرس الطلاب أكثر، فإنهم يميلون إلى الأداء بشكل أفضل في الامتحانات.

ومع ذلك، لنفترض أننا نقوم فقط بجمع البيانات عن الطلاب في دورات الشرف. من الممكن أن يكون جميع هؤلاء الطلاب قد درسوا لمدة 6 ساعات على الأقل.

لذا، إذا قمنا بحساب الارتباط بين ساعات الدراسة ودرجات الامتحانات لهؤلاء الطلاب، فسنستخدم نطاقًا ضيقًا للساعات المتغيرة التي تمت دراستها .

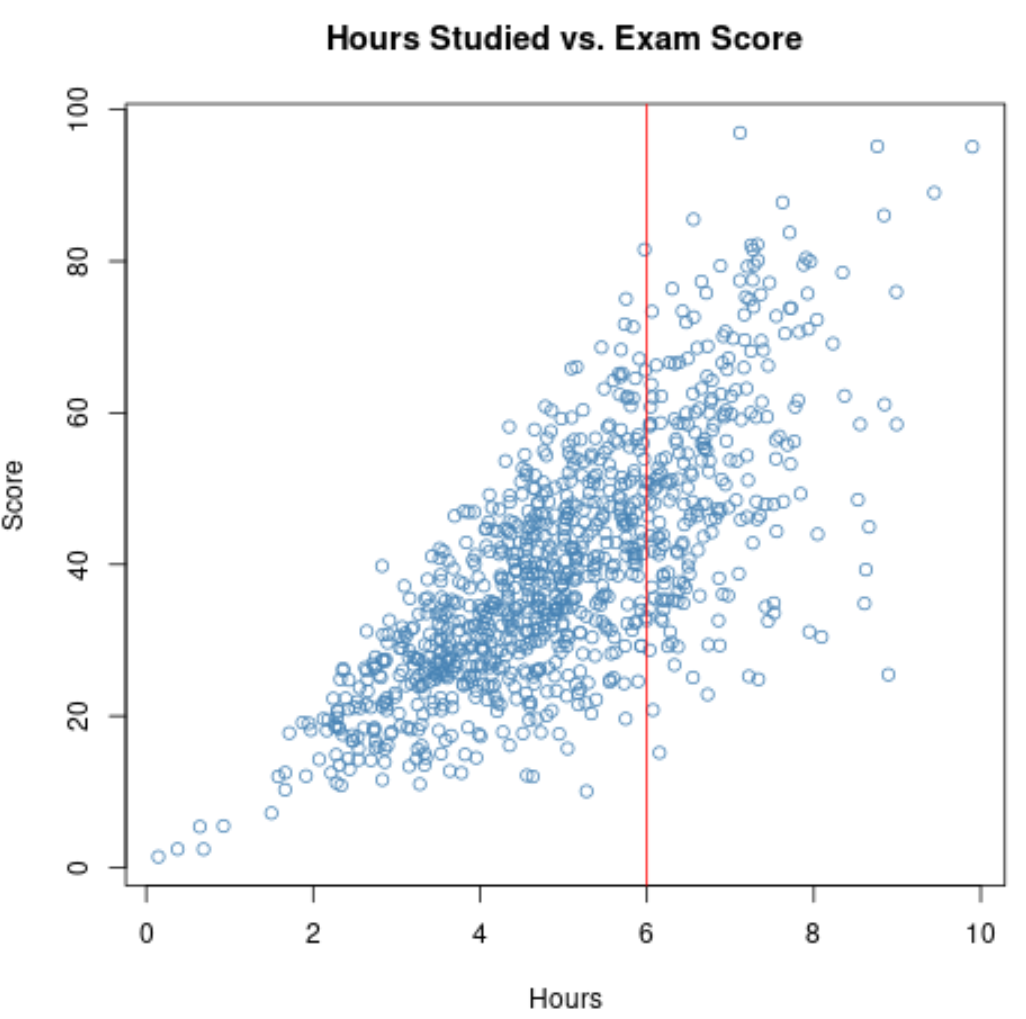
إذا قمنا بتكبير مخطط التشتت للنطاق الذي تكون فيه الساعات أكبر من 6، فهذا ما يبدو عليه المخطط:

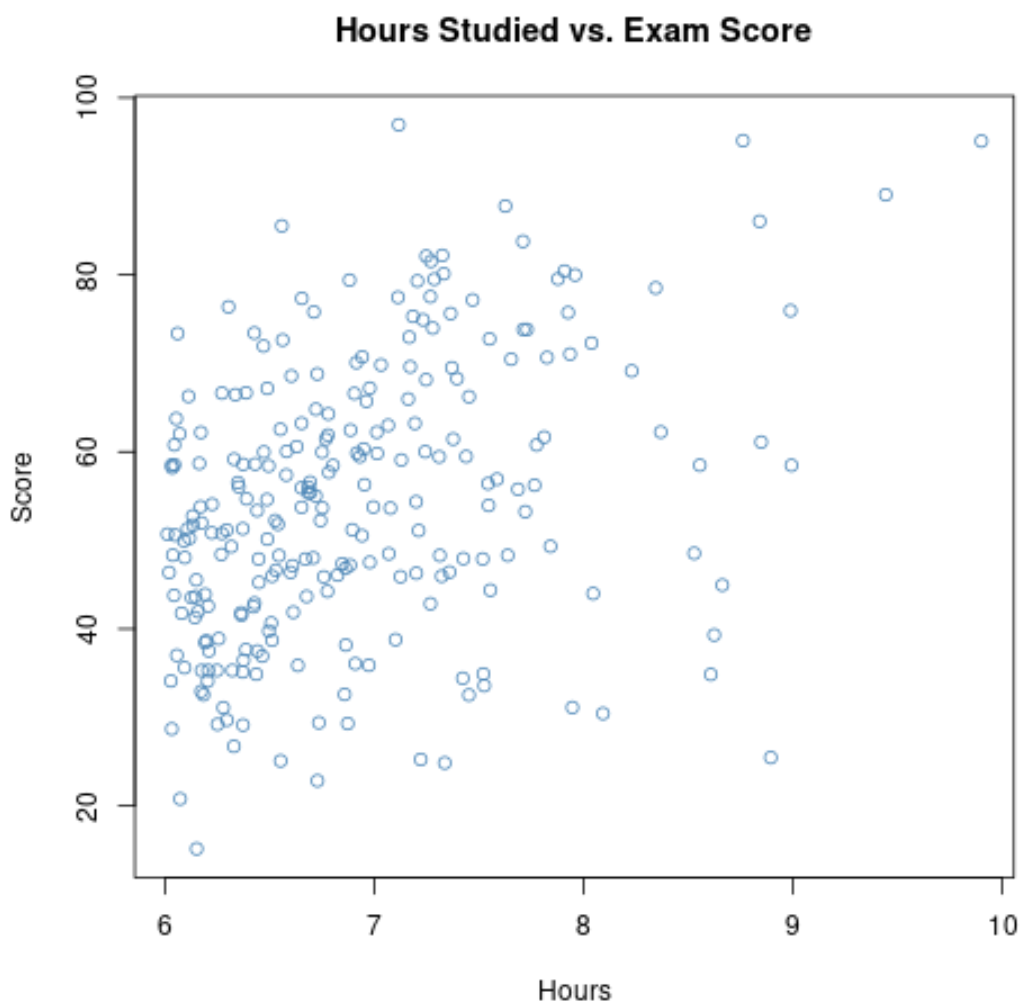
وتبين أن الارتباط بين المتغيرين على هذا الرسم البياني هو 0.37 ، وهو أقل بكثير من 0.73 .

وبالتالي، إذا قمنا فقط بجمع بيانات عن ساعات الدراسة ودرجات الامتحانات للطلاب في مقررات الشرف، فقد نفترض أن هناك علاقة ضعيفة بين ساعات الدراسة ودرجات الامتحانات.

ومع ذلك، فإن هذه النتيجة ستكون مضللة لأننا استخدمنا نطاقًا مقيدًا لأحد المتغيرات.

أمثلة من العالم الحقيقي للنطاق المحدود

يمكن أن تنشأ مشكلة النطاق المحدود عمليًا في العديد من الدراسات البحثية المختلفة. وهنا بعض الأمثلة:

1. دراسات على الرياضيين ذوي الأداء العالي . قد يكون الباحثون مهتمين بدراسة ما إذا كان برنامج تدريبي معين ينتج كتلة عضلية أكبر من برنامج قياسي معين.

إذا قام الباحثون بجمع بيانات عن الرياضيين النخبة فقط، فمن المحتمل أن هؤلاء الرياضيين لديهم بالفعل كتلة عضلية عالية. وبالتالي سيكون هناك نطاق ضيق من القيم المتاحة لحساب العلاقة بين البرنامج التدريبي وكتلة العضلات المنتجة.

2. دراسات الطلاب المتفوقين. قد يرغب الباحثون في دراسة ما إذا كان برنامج معين من الدروس الخصوصية له تأثير إيجابي على الدرجات أم لا. بطبيعتها، الطلاب الذين يتوقون إلى تحسين درجاتهم والمشاركة في برنامج الدروس الخصوصية قد يكونون بالفعل طلابًا متفوقين.

لذلك قد لا يكون هناك مجال كبير للتحسين في درجات هؤلاء الطلاب. عندما يقوم الباحثون بحساب الارتباط بين الساعات التي يقضيها الطلاب في برنامج الدروس الخصوصية وزيادة الدرجات الناتجة، فقد يتم التقليل من أهمية الارتباط الحقيقي لأن مجال تحسين الدرجات كان محدودًا.

كيفية حساب النطاقات المقيدة

تُعرف إحدى الطرق الشائعة لحساب النطاقات المقيدة باسم حالة ثورندايك 2 ، وهي صيغة طورها عالم القياس النفسي روبرت إل. ثورندايك.

توفر هذه الصيغة تقديرًا للارتباط الحقيقي بين متغيرين وتستخدم الحساب التالي:

الارتباط الحقيقي = √(1-(SD ² _{y مقيد} -SD ² _{y غير مقيد} )) * (1-r ² _مقيد )

ذهب:

• SD ² _{المقيّد y} : الانحراف المعياري التربيعي للبيانات المتوفرة حول متغير الاستجابة y.
• _Unrestricted SD ² y: الانحراف المعياري المربع المعروف لمتغير الاستجابة للسكان.
• r ² _مقيد : الارتباط التربيعي على البيانات المقيدة المتاحة.

لقد ثبت أن هذه الصيغة فعالة في إنتاج تقديرات غير متحيزة للارتباط الحقيقي بين متغيرين عندما يعاني أحد المتغيرات من نطاق مقيد.

لاحظ أنه لاستخدام هذه الصيغة، يجب أن يكون لديك تقدير للانحراف المعياري السكاني الحقيقي لمتغير الاستجابة.