التحيز المتغير المحذوف: التعريف والأمثلة
يحدث انحياز المتغير المحذوف عندما لا يتم تضمين متغير توضيحي ذي صلة في نموذج الانحدار ، مما قد يؤدي إلى انحياز في معامل واحد أو أكثر من المتغيرات التوضيحية في النموذج.
غالبًا ما يتم استبعاد المتغير المحذوف من نموذج الانحدار لأحد السببين:
1. بيانات المتغير غير متوفرة ببساطة.
2. تأثير المتغير التوضيحي على متغير الاستجابة غير معروف.
لكي يقوم المتغير المحذوف بتشويه معاملات النموذج فعليًا، يجب استيفاء الشرطين التاليين:
1. يجب أن يكون المتغير المحذوف مرتبطا بواحد أو أكثر من المتغيرات التوضيحية في النموذج.
2. يجب أن يكون المتغير المحذوف مرتبطا بمتغير الاستجابة في النموذج.
آثار التحيز المتغير المحذوف
لنفترض أن لدينا متغيرين توضيحيين، A وB، ومتغير استجابة، Y. لنفترض أننا قمنا بتركيب نموذج انحدار خطي بسيط مع A باعتباره المتغير التوضيحي الوحيد وتركنا B خارج النموذج.
إذا كان B مرتبطًا بـ A ومرتبطًا بـ Y، فسيؤدي ذلك إلى انحياز في تقدير معامل A. ويوضح الرسم البياني التالي كيف سيكون تقدير معامل A متحيزًا، اعتمادًا على طبيعة العلاقة مع ب:
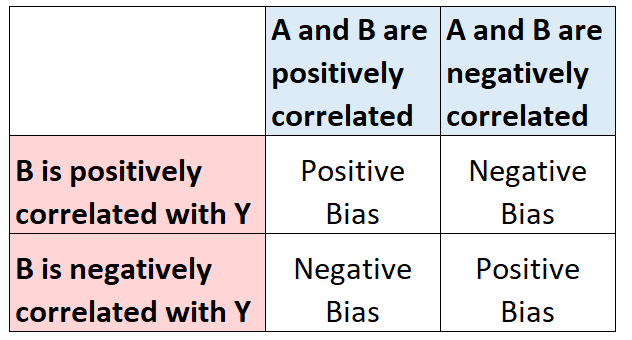
مثال: التحيز المتغير المحذوف
لنفترض أننا نريد دراسة تأثير المساحة بالقدم المربع على سعر العقار وبالتالي قمنا بتطبيق نموذج الانحدار الخطي البسيط التالي:
سعر المنزل = ب 0 + ب 1 (مساحة مربعة)
لنفترض أننا وجدنا أن النموذج المقدر هو:
سعر المنزل = 40,203.91 + 118.31 (مساحة مربعة)
الطريقة التي نفسر بها معامل القدم المربع هي أن كل زيادة إضافية بمقدار وحدة واحدة في القدم المربع ترتبط بزيادة في سعر المنزل بمقدار 118.31 دولارًا في المتوسط.
ومع ذلك، لنفترض أننا تركنا المتغير التوضيحي للعمر والذي تبين أنه يرتبط ارتباطًا سلبيًا قويًا بالقدم المربع ويرتبط ارتباطًا سلبيًا قويًا بسعر العقارات. يجب أن يكون هذا المتغير موجودًا في النموذج، لكنه ليس كذلك. وبالتالي، من المرجح أن يكون تقدير المعامل للقدم المربع متحيزًا.
نظرًا لأن العمر يرتبط سلبًا بكل من المتغير التوضيحي ومتغير الاستجابة في النموذج، فإننا نتوقع أن يكون تقدير المعامل للقدم المربع متحيزًا بشكل إيجابي:
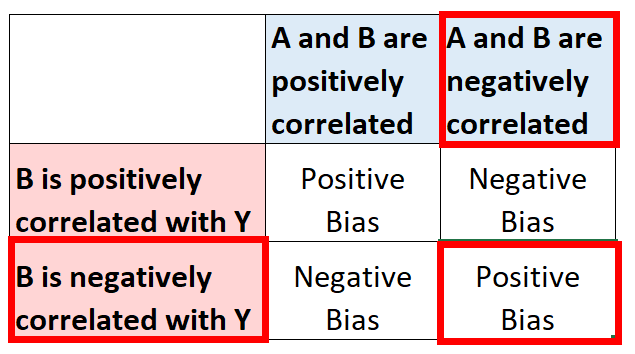
لنفترض أننا وجدنا بيانات عن عمر المسكن ثم قمنا بإدراجها في النموذج. فيصبح النموذج بعد ذلك:
سعر المنزل = ب 0 + ب 1 (مساحة مربعة) + ب 2 (العمر)
لنفترض أننا وجدنا أن النموذج المقدر هو:
سعر المنزل = 123,426.20 + 81.06 (مساحة مربعة) – 1,291.04 (العمر)
لاحظ أن تقدير المعامل للقدم المربع قد انخفض بشكل ملحوظ، مما يعني أنه كان متحيزًا بشكل إيجابي في النموذج السابق.
الطريقة التي نفسر بها معامل القدم المربع في هذا النموذج هي أن كل زيادة إضافية بمقدار وحدة واحدة في القدم المربع ترتبط بمتوسط زيادة في سعر المنزل قدره 81.06 دولارًا، على افتراض أن العمر يظل ثابتًا.
ما يجب القيام به بشأن التحيز المتغير المحذوف
لسوء الحظ، غالبًا ما يحدث انحياز المتغير المحذوف في العالم الحقيقي لأنه يجب عمومًا تضمين بعض المتغيرات في نموذج الانحدار، ولكن ليس بسبب عدم توفر البيانات الخاصة بها أو أن العلاقة بينها وبين متغير الاستجابة غير معروفة.
إذا أمكن، يجب عليك محاولة تضمين جميع المتغيرات التوضيحية ذات الصلة في نموذج الانحدار حتى تتمكن من فهم العلاقة الحقيقية بين المتغيرات التوضيحية ومتغير الاستجابة.
إن استبعاد المتغيرات التوضيحية ذات الصلة من النموذج يمكن أن يؤثر بشكل كبير على تفسير النموذج، كما رأينا في المثال السابق مع أسعار العقارات.
مصادر إضافية
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر