توزيع العينات
تشرح هذه المقالة ما هو توزيع العينات في الإحصائيات وما يتم استخدامه من أجله. لذا ستجد معنى توزيع العينات، ومثالًا ملموسًا لتوزيع العينات، بالإضافة إلى الصيغ الخاصة بأنواع توزيعات العينات الأكثر شيوعًا.
ما هو توزيع العينات؟
توزيع العينات ، أو توزيع العينات ، هو التوزيع الذي ينتج عن النظر في جميع العينات الممكنة من مجتمع ما. بمعنى آخر، توزيع العينات هو التوزيع الذي يتم الحصول عليه عن طريق حساب معلمة أخذ العينات لجميع العينات الممكنة من مجتمع ما.
على سبيل المثال، إذا استخرجنا جميع العينات الممكنة من مجتمع إحصائي وقمنا بحساب متوسط كل عينة، فإن مجموعة متوسطات العينة تشكل توزيع العينات. بتعبير أدق، بما أن المعلمة المحسوبة هي الوسط الحسابي، فهي توزيع المعاينة للمتوسط.
في الإحصاء، يتم استخدام توزيع العينات لحساب احتمالية الاقتراب من قيمة المعلمة السكانية عند دراسة عينة واحدة. وبالمثل، فإن توزيع العينات يسمح لنا بتقدير خطأ أخذ العينات لحجم عينة معين.
مثال لتوزيع العينات
الآن بعد أن عرفنا تعريف توزيع العينات، دعونا نلقي نظرة على مثال بسيط لفهم المفهوم بشكل كامل.
- في صندوق نضع ثلاث كرات ولكل واحدة رقم مكتوب من واحد إلى ثلاثة، بحيث تكون كرة واحدة تحمل الرقم 1 وكرة أخرى تحمل الرقم 2 والكرة الأخيرة تحمل الرقم 3. لعينة حجمها n = 2، يحسب احتمالات توزيع العينات للمتوسط إذا تم اختيار العينات مع الاستبدال.
يتم اختيار العينات مع الاستبدال، أي أن الكرة التي تم التقاطها لتحديد العنصر الأول من العينة يتم إرجاعها إلى الصندوق ويمكن اختيارها مرة أخرى أثناء الاستخراج الثاني. ولذلك فإن جميع العينات الممكنة من السكان هي:
1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3
وهكذا نحسب الوسط الحسابي لكل عينة ممكنة:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ولذلك فإن احتمالات الحصول على كل قيمة من متوسطات العينة عند اختيار عينة عشوائية من المجتمع هي كما يلي:
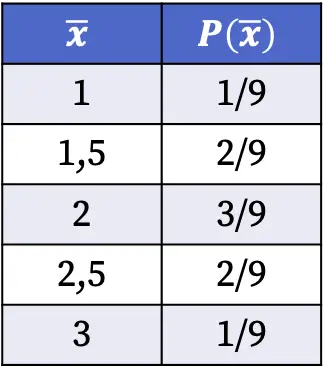
تم حساب احتمالات توزيع العينات الموضحة في الجدول أعلاه بقسمة عدد العينات ذات القيمة المتوسطة المذكورة على إجمالي عدد الحالات المحتملة. على سبيل المثال: متوسط العينة هو 1.5 في حالتين من أصل تسع حالات محتملة، وبالتالي P(1.5)=2/9.
أنواع توزيعات العينات
يمكن تصنيف توزيعات العينات (أو توزيعات العينات) بناءً على معلمة أخذ العينات التي تم الحصول عليها منها. لذا فإن أكثر أنواع التوزيعات شيوعًا هي كما يلي:
- توزيع المعاينة للمتوسط : هو توزيع المعاينة الناتج عن حساب الوسط الحسابي لكل عينة.
- التوزيع النسبي للعينات : هو توزيع العينات الذي يتم الحصول عليه عن طريق حساب نسبة جميع العينات.
- توزيع عينات التباين : هذا هو توزيع العينات الذي يشكل مجموعة جميع التباينات في العينة.
- اختلاف وسائل توزيع العينات : هو توزيع العينات الناتج عن حساب الفرق بين متوسطات جميع العينات الممكنة من مجتمعين مختلفين.
- الفرق في توزيع العينات بالنسب : هو توزيع العينات الذي يتم الحصول عليه عن طريق طرح جميع نسب العينات الممكنة من مجموعتين من السكان.
يتم شرح كل نوع من أنواع توزيع العينات بمزيد من التفصيل أدناه.
توزيع العينات للمتوسط
بالنظر إلى السكان الذين يتبعون التوزيع الاحتمالي الطبيعي مع المتوسط
![]()
والانحراف المعياري
![]()
ويتم استخراج عينات الحجم
![]()
، سيتم أيضًا تحديد توزيع المعاينة للمتوسط من خلال التوزيع الطبيعي الذي يتميز بالخصائص التالية:
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
ذهب
![]()
هو متوسط توزيع العينات للمتوسط و
![]()
هو انحرافه المعياري. بالإضافة إلى،
![]()
هو الخطأ المعياري لتوزيع العينات.
ملحوظة: إذا كان المجتمع لا يتبع التوزيع الطبيعي ولكن حجم العينة كبير (ن > 30)، فيمكن أيضًا تقريب توزيع المعاينة للمتوسط إلى التوزيع الطبيعي أعلاه بواسطة حد النظرية المركزية.
لذلك، بما أن توزيع المعاينة للمتوسط يتبع التوزيع الطبيعي، فإن صيغة حساب أي احتمال متعلق بمتوسط العينة هي:

ذهب:
-

هي وسيلة العينة.
-

هذا هو متوسط عدد السكان.
-

هو الانحراف المعياري للسكان.
-

هو حجم العينة.
-

هو متغير يحدده التوزيع الطبيعي القياسي N(0,1).
توزيع العينات نسبة
في الواقع، عندما ندرس نسبة من العينة، فإننا نقوم بتحليل حالات النجاح. ولذلك فإن المتغير العشوائي في الدراسة يتبع التوزيع الاحتمالي ذي الحدين.
وفقًا لنظرية الحد المركزي، بالنسبة للأحجام الكبيرة (n>30) يمكننا تقريب التوزيع ذي الحدين من التوزيع الطبيعي. ولذلك، فإن توزيع المعاينة للنسبة يقترب من التوزيع الطبيعي مع المعلمات التالية:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
ذهب
![]()
هو احتمال النجاح و
![]()
هو احتمال الفشل
![]()
.
ملاحظة: لا يمكن تقريب التوزيع ذي الحدين إلى التوزيع الطبيعي إلا إذا كان

![]()
و
![]()
.
لذلك، بما أن توزيع المعاينة للنسبة يمكن تقريبه إلى التوزيع الطبيعي، فإن صيغة حساب أي احتمال متعلق بنسبة العينة هي:

ذهب:
-

هي نسبة العينة
-

هي النسبة من السكان.
-

هو احتمال فشل السكان،

.
-

هو حجم العينة.
-

هو متغير يحدده التوزيع الطبيعي القياسي N(0,1).
توزيع عينات التباين
يتم تعريف توزيع عينات التباين من خلال توزيع احتمالية مربع كاي. ولذلك فإن صيغة إحصائية توزيع التباين في العينة هي:
![]()
ذهب:
-

هي إحصائية توزيع عينات التباين، والتي تتبع توزيع مربع كاي.
-

هو حجم العينة.
-

هو تباين العينة.
-

هو التباين السكاني.
توزيع العينات لفرق الوسائل
إذا كان حجم العينة كبيرًا بدرجة كافية (n 1 ≥30 وn 2 ≥30)، فإن توزيع المعاينة لفرق المتوسط يتبع التوزيع الطبيعي. وبشكل أكثر دقة، يتم حساب معلمات التوزيع المذكور على النحو التالي:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
ملحوظة: إذا كان كلا المجموعتين توزيعات طبيعية، فإن توزيع العينة للفرق في المتوسطات يتبع التوزيع الطبيعي بغض النظر عن أحجام العينات.
لذلك، بما أن توزيع المعاينة للفرق في المتوسطات يتم تحديده بالتوزيع الطبيعي، فإن صيغة حساب إحصائية توزيع المعاينة للفرق في المتوسطات هي:

ذهب:
-

هو متوسط العينة i.
-

هو متوسط عدد السكان أنا.
-

هو الانحراف المعياري للسكان أنا.
-

هو حجم العينة أنا.
-

هو متغير يحدده التوزيع الطبيعي القياسي N(0,1).
لاحظ أن العينات من مجموعات سكانية مختلفة قد يكون لها أحجام عينات مختلفة.
توزيع العينات من الفرق في النسب
يتم تحديد العينات المختارة للاختلاف في نسب توزيع العينات من خلال التوزيعات ذات الحدين، لأنه للأغراض العملية فإن النسبة هي نسبة حالات النجاح إلى العدد الإجمالي للملاحظات.
ومع ذلك، بسبب نظرية الحد المركزي، يمكن تقريب التوزيعات ذات الحدين إلى التوزيعات الاحتمالية العادية. ولذلك يمكن تقريب توزيع المعاينة للفرق في النسب إلى توزيع طبيعي يتمتع بالخصائص التالية:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
ملاحظة: لا يمكن تقريب توزيع العينة للفرق في النسب إلا إذا كان
![]()
,
![]()
,
![]()
,
![]()
,
![]()
و
![]()
.
لذلك، بما أن توزيع المعاينة للفرق في النسب يمكن تقريبه إلى التوزيع الطبيعي، فإن صيغة حساب إحصائية توزيع المعاينة للفرق في النسب هي كما يلي:

ذهب:
-

هي نسبة العينة أنا.
-

هي نسبة السكان ط.
-

هو احتمال فشل السكان أنا ،

.
-

هو حجم العينة أنا.
-

هو متغير يحدده التوزيع الطبيعي القياسي N(0,1).