توزيع العينات لفرق الوسائل
تشرح هذه المقالة ما هو توزيع العينات للفرق بين وسيلتين في الإحصائيات. ستجد أيضًا صيغة توزيع العينات لفرق الوسائل، بالإضافة إلى تمرين تم حله خطوة بخطوة.
ما هو توزيع العينة لفرق الوسائل؟
توزيع المعاينة للفرق في المتوسطات هو التوزيع الناتج عن حساب الفروق بين متوسطات جميع العينات الممكنة من مجتمعين مختلفين.
أي أنه للحصول على توزيع المعاينة للفرق في المتوسطات، يجب اختيار جميع العينات الممكنة من مجتمعي الدراسة، ثم يتم حساب متوسط كل عينة مختارة، وأخيرا، الفرق بين جميع المتوسطات المحسوبة من المجتمعين. وبالتالي فإن مجموعة القيم التي تم الحصول عليها بعد تطبيق كل هذه العمليات تشكل توزيع المعاينة لفرق المتوسطات.

يتم استخدام الفرق في توزيع عينات العينات لحساب احتمال أن يكون الفرق بين وسيلتين لعينات تم اختيارها عشوائيًا من مجتمعين مختلفين قريبًا من الفرق في متوسطات السكان.
صيغة لتوزيع العينات لفرق الوسائل
إذا كان حجم العينة كبيرًا بدرجة كافية (n 1 ≥30 وn 2 ≥30)، فإن توزيع المعاينة للفرق في المتوسطات يتبع التوزيع الطبيعي. وبشكل أكثر دقة، يتم حساب معلمات التوزيع المذكور على النحو التالي:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
ملحوظة: إذا كان كلا المجتمعين توزيعين طبيعيين ، فإن توزيع العينة للفرق في المتوسطات يتبع التوزيع الطبيعي بغض النظر عن أحجام العينات.
لذلك، بما أن توزيع المعاينة للفرق في المتوسطات يتم تحديده بالتوزيع الطبيعي، فإن صيغة حساب إحصائية توزيع المعاينة للفرق في المتوسطات هي:

ذهب:
-

هو متوسط العينة i.
-

هو متوسط عدد السكان أنا.
-

هو الانحراف المعياري للسكان أنا.
-

هو حجم العينة أنا.
-

هو متغير يحدده التوزيع الطبيعي القياسي N(0,1).
لاحظ أن العينات من مجموعات سكانية مختلفة قد يكون لها أحجام عينات مختلفة.
مثال ملموس لتوزيع العينات لفرق الوسائل
وبمجرد أن نتعرف على تعريف اختلاف متوسطات توزيع المعاينة وما هي صيغته، سنرى مثالاً خطوة بخطوة للانتهاء من فهم مفهوم اختلاف متوسطات توزيع المعاينة.
- في دراسة إحصائية، نريد تحليل الفرق بين طول الأولاد والبنات في عمر معين. نحن نعلم أن التوزيع الذي يحدد عدد السكان من الذكور في هذا العمر يبلغ متوسطه 157 سم وانحراف معياري قدره 9 سم، ومن ناحية أخرى، فإن التوزيع الذي يحدد عدد الفتيات في هذا العمر يبلغ متوسطه 148 سم والانحراف المعياري 7 سم. إذا تم اختيار عينة مكونة من 30 ولدًا في هذا العمر وعينة مكونة من 35 فتاة في هذا العمر، فما احتمال أن يكون متوسط طول عينة الأولاد أكبر بمقدار 12 سم من متوسط طول عينة البنات؟
لحل هذه المشكلة، أول ما يجب فعله هو حساب إحصائية الفرق في توزيع المعاينة. لذلك نطبق الصيغة الموضحة أعلاه:
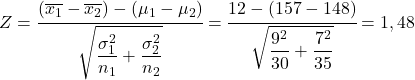
ولذلك، فإن احتمال أن يكون متوسط ارتفاع عينة الأولاد أكبر بمقدار 12 سم من متوسط طول الفتيات يعادل احتمال أن يكون المتغير Z أكبر من 1.48.
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p>
</p>
<p style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-683cd2a72980115d8d18c906d619370a_l3.png) لذلك نبحث عن احتمال Z>1.48 في جدول Z :
لذلك نبحث عن احتمال Z>1.48 في جدول Z :
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p>
</p>
<p style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5b83fdc11bd2320249679c4752660451_l3.png) باختصار، فإن احتمال أن يكون متوسط طول عينة الأولاد أكبر بمقدار 12 سم من متوسط طول الفتيات هو 6.94%.
باختصار، فإن احتمال أن يكون متوسط طول عينة الأولاد أكبر بمقدار 12 سم من متوسط طول الفتيات هو 6.94%.