توزيع العينات للمتوسط
تشرح هذه المقالة ما هو توزيع العينات للمتوسط في الإحصائيات. ستجد أيضًا معادلة متوسط توزيع العينات وتمرينًا تم حله خطوة بخطوة.
ما هو توزيع العينات للمتوسط؟
توزيع المعاينة للمتوسط (أو توزيع المعاينة للوسائل ) هو التوزيع الناتج عن حساب متوسط المعاينة لكل عينة محتملة من مجتمع ما. أي أن مجموعة متوسطات العينة من جميع العينات الممكنة من مجتمع ما تشكل توزيع المعاينة للمتوسط.
أو بمعنى آخر، إذا قمنا بدراسة جميع العينات التي يمكن أخذها من مجتمع ما وحساب متوسط كل عينة، فإن مجموعة القيم المحسوبة تشكل توزيعاً اعتيانياً لمتوسط العينة.
في الإحصاء، يتم استخدام توزيع المعاينة للمتوسط لحساب احتمالية الاقتراب من قيمة متوسط المجتمع عند تحليل عينة واحدة.
صيغة لتوزيع العينات للمتوسط
بالنظر إلى السكان الذين يتبعون التوزيع الاحتمالي الطبيعي مع المتوسط
![]()
والانحراف المعياري
![]()
ويتم استخراج عينات الحجم
![]()
، سيتم أيضًا تحديد توزيع المعاينة للمتوسط من خلال التوزيع الطبيعي الذي يتميز بالخصائص التالية:
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
ذهب
![]()
هو متوسط توزيع العينات للمتوسط و
![]()
هو انحرافه المعياري. بالإضافة إلى،
![]()
هو الخطأ المعياري لتوزيع العينات.
ملاحظة: إذا كان السكان لا يتبعون التوزيع الطبيعي ولكن حجم العينة كبير (ن > 30)، فيمكن أيضًا تقريب توزيع المعاينة للمتوسط إلى التوزيع الطبيعي السابق بواسطة نظرية الحد المركزي.
لذلك، بما أن توزيع المعاينة للمتوسط يتبع التوزيع الطبيعي، فإن صيغة حساب أي احتمال متعلق بمتوسط العينة هي:

ذهب:
-

هي وسيلة العينة.
-

هذا هو متوسط عدد السكان.
-

هو الانحراف المعياري للسكان.
-

هو حجم العينة.
-

هو متغير يحدده التوزيع الطبيعي القياسي N(0,1).
مثال من العالم الحقيقي لتوزيع العينات للمتوسط
بعد الاطلاع على تعريف توزيع المعاينة للمتوسط وما هي الصيغ المرتبطة به، دعونا نحل مثالاً لفهم المفهوم بشكل أفضل.
- ويتبع وزن طلاب الجامعة توزيعا طبيعيا بمتوسط 68 كجم وانحراف معياري 9 كجم. عازم:
- ما احتمال أن يكون متوسط عينة عشوائية مكونة من 25 طالبًا أقل من 66 كجم؟
- إذا تم أخذ 300 عينة يبلغ حجم كل منها 25 طالبًا، فما عدد متوسطات العينات التي تقل قيمتها عن 66 كجم؟
أولًا، يجب علينا حساب قيمة الإحصائية المقابلة، ولهذا نطبق الصيغة التي رأيناها أعلاه:
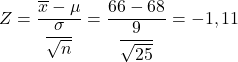
وبالتالي فإن الاحتمال الذي نبحث عنه هو ما يتوافق مع القيمة Z=-1.11 للذيل الأيسر للتوزيع الطبيعي القياسي، والذي يمكن الحصول عليه بسهولة من جدول احتمالات Z. لذلك نستخدم الجدول Z لتحديد احتمال أن تطلب منا المشكلة:
![]()
الآن بعد أن عرفنا احتمال أن يكون متوسط العينة العشوائية أقل من 66 كجم، لمعرفة متوسط عدد العينات أقل من 66 كجم مع 300 عينة متساوية، نحتاج إلى ضرب الاحتمال المحسوب في العدد الإجمالي للعينات المأخوذة:
![]()
ولذلك، فإن ما يقرب من 40 من العينات المستخرجة سيكون متوسط وزنها أقل من 66 كجم.