مقدمة لتوزيع رايلي

توزيع رايلي هو توزيع احتمالي مستمر يستخدم لنمذجة المتغيرات العشوائية التي يمكن أن تأخذ قيمًا تساوي أو أكبر من الصفر فقط.

لديها وظيفة كثافة الاحتمال التالية:

و(س; σ) = (س/σ ² )ه ^{-x 2 /(2σ 2 )}

حيث σ هي معلمة مقياس التوزيع.

خصائص توزيع رايلي

يتميز توزيع رايلي بالخصائص التالية:

• المتوسط: σ√ π/2
• الانحراف: ((4-π)/2)σ ²
• الوضع: σ

بما أن π لها قيمة عددية معروفة، فيمكننا تبسيط الخصائص كما يلي:

• المتوسط: 1.253σ
• الانحراف: 0.429σ ²
• الوضع: σ

تصور توزيع رايلي

ويوضح الرسم البياني التالي شكل توزيع رايلي حيث يأخذ قيمًا مختلفة لمعلمة المقياس:

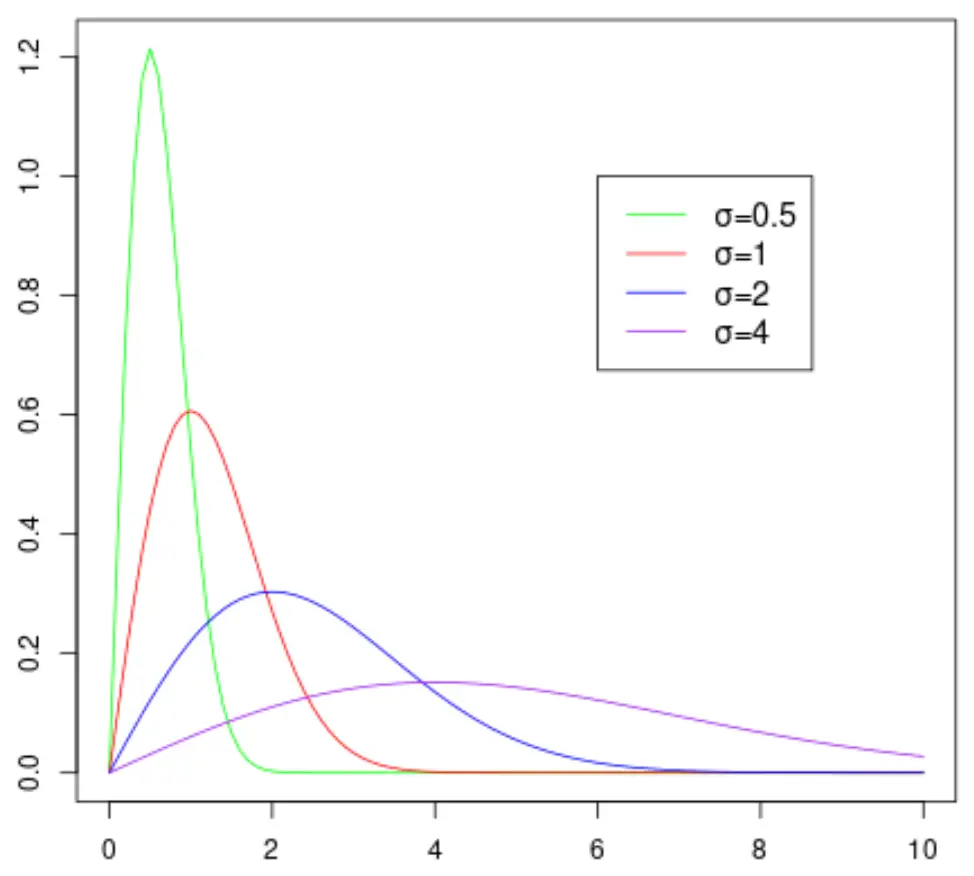
لاحظ أنه كلما زادت قيمة معلمة المقياس σ، أصبح التوزيع أوسع.

المكافأة: بالنسبة لأولئك الذين لديهم فضول، استخدمنا كود R التالي لإنشاء الرسم البياني أعلاه:

 #load VGAM package
library (VGAM)

#create density plots
curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green')
curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE)
curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE)
curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE)

#add legend
legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"),
       col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)

العلاقة مع التوزيعات الأخرى

توزيع رايلي له العلاقة التالية مع التوزيعات الاحتمالية الأخرى:

1. عندما تكون معلمة المقياس (σ) تساوي 1، فإن توزيع رايلي يساوي توزيع مربع كاي مع درجتين من الحرية.

2. توزيع رايلي هو حالة خاصة من توزيع ويبل مع معلمة الشكل k = 2.

3. توزيع رايلي بمعلمة المقياس σ يساوي توزيع رايس مع رايس (0، σ).

التطبيقات

ومن الناحية العملية، يتم استخدام توزيع رايلي في تطبيقات مختلفة، بما في ذلك:

1. يستخدم توزيع رايلي لنمذجة سلوك الأمواج في المحيط، بما في ذلك الوقت الذي تستغرقه الأمواج للوصول إلى ذروتها والحد الأقصى للارتفاع الذي وصلت إليه الأمواج.

2. يُستخدم توزيع رايلي لنمذجة سلوك بيانات الخلفية في التصوير بالرنين المغناطيسي، والمعروف أكثر باسم التصوير بالرنين المغناطيسي.

3. يستخدم توزيع رايلي في مجال التغذية لنمذجة العلاقة بين مستويات العناصر الغذائية والاستجابة الغذائية لدى الإنسان والحيوان.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول التوزيعات الأخرى في الإحصائيات:

مقدمة للتوزيع الطبيعي
مقدمة للتوزيع ذي الحدين
مقدمة لتوزيع بواسون