توزيع سنديكور f
تشرح هذه المقالة ماهية توزيعة Snedecor F وفيم يتم استخدامها. بالإضافة إلى ذلك، ستتمكن من رؤية الرسم البياني لتوزيع Snedecor F وما هي خصائصه الإحصائية.
ما هو توزيع Snedecor F؟
توزيع Snedecor F ، ويسمى أيضًا توزيع Fisher-Snedecor F أو ببساطة توزيع F ، هو توزيع احتمالي مستمر يستخدم في الاستدلال الإحصائي، وخاصة في تحليل التباين.
إحدى خصائص توزيع Snedecor F هي أنه يتم تعريفه بقيمة معلمتين حقيقيتين، m و n ، اللتين تشيران إلى درجات الحرية الخاصة بهما. وبالتالي، فإن رمز توزيع Snedecor F هو F m,n ، حيث m و n هما المعلمتان اللتان تحددان التوزيع.
 رياضياً، توزيع Snedecor F يساوي حاصل القسمة بين توزيع كاي مربع واحد ودرجات حريته مقسوماً على حاصل القسمة بين توزيع مربع كاي آخر ودرجات حريته. وبالتالي، فإن الصيغة التي تحدد توزيع Snedecor F هي كما يلي:
رياضياً، توزيع Snedecor F يساوي حاصل القسمة بين توزيع كاي مربع واحد ودرجات حريته مقسوماً على حاصل القسمة بين توزيع مربع كاي آخر ودرجات حريته. وبالتالي، فإن الصيغة التي تحدد توزيع Snedecor F هي كما يلي:
![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
يرجع اسم توزيع Fisher-Snedecor F إلى الإحصائي الإنجليزي رونالد فيشر والإحصائي الأمريكي جورج سنيديكور.
في الإحصاء، توزيع Fisher-Snedecor F له تطبيقات مختلفة. على سبيل المثال، يتم استخدام توزيع Fisher-Snedecor F لمقارنة نماذج الانحدار الخطي المختلفة، ويستخدم هذا التوزيع الاحتمالي في تحليل التباين (ANOVA).
مخطط توزيع Snedecor F
بمجرد أن رأينا تعريف توزيع Snedecor F، يظهر أدناه الرسم البياني لدالة الكثافة والرسم البياني لاحتمالها التراكمي.
في الرسم البياني أدناه يمكنك رؤية عدة أمثلة لتوزيعات Snedecor F بدرجات مختلفة من الحرية.
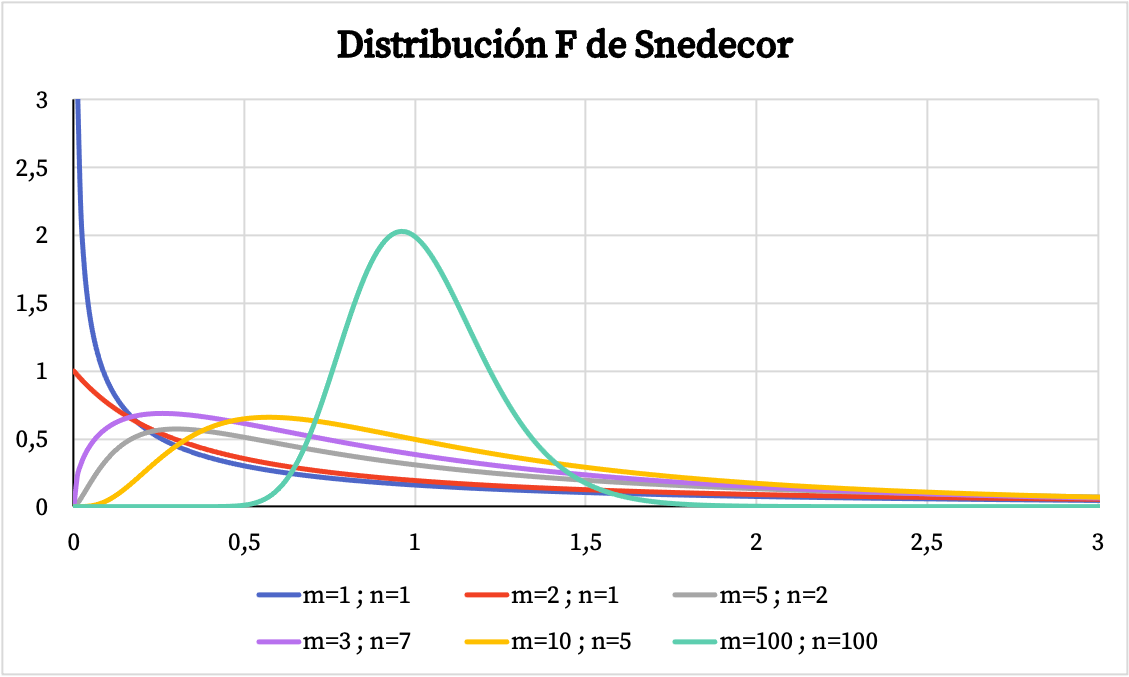
من ناحية أخرى، في الرسم البياني أدناه يمكنك أن ترى كيف يختلف الرسم البياني لدالة الاحتمال التراكمي لتوزيع Snedecor F اعتمادًا على قيمه المميزة.
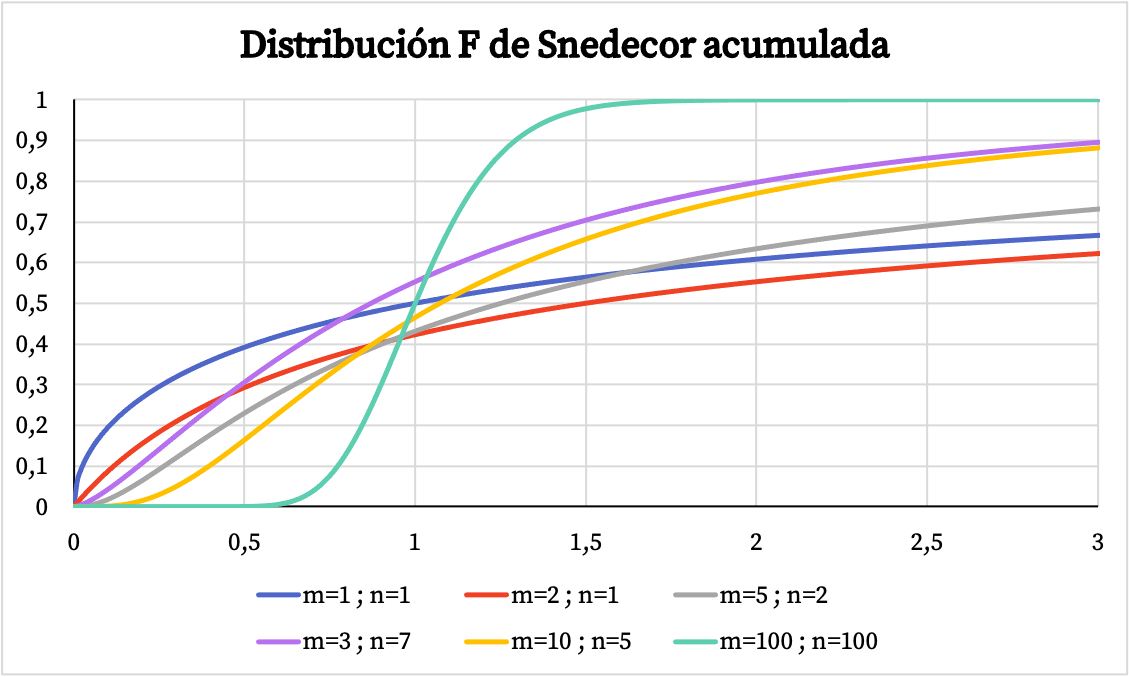
خصائص توزيعة Snedecor F
وأخيرا، يعرض هذا القسم أهم خصائص توزيعة Snedecor F.
- درجات الحرية لتوزيع Snedecor F، m و n ، هما معلمتان تحددان شكل التوزيع. هذه القيم المميزة لتوزيع Snedecor F هي أعداد صحيحة موجبة.
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p>
</p>
<ul style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- بالنسبة للقيم n أكبر من 2، فإن متوسط توزيع Snedecor F يساوي n عند طرح n ناقص 2.
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<ul style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p>
</p>
<ul style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
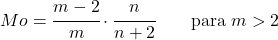
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- إذا كان المتغير يتبع توزيع Snedecor F بدرجات الحرية m و n ، فإن عكس المتغير المذكور يتبع توزيع Snedecor F بنفس درجات الحرية ولكن مع تغيير ترتيب قيمه.
![]()
- توزيعة الطالب لها العلاقة التالية مع توزيعة Snedecor F:
![]()