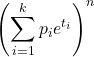توزيع متعدد الحدود

By دكتور بنيامين أندرسون زومار 4, 2023 احتمالا 0 Comments

تشرح هذه المقالة ما هو التوزيع متعدد الحدود في الإحصائيات. لذلك، ستجد تعريف التوزيع متعدد الحدود، ما هي صيغته، تمرين محلول وما هي خصائص هذا النوع من التوزيع الاحتمالي. بالإضافة إلى ذلك، سوف تكون قادرًا على حساب احتمال التوزيع متعدد الحدود باستخدام الآلة الحاسبة عبر الإنترنت.

ما هو التوزيع متعدد الحدود؟

التوزيع متعدد الحدود (أو التوزيع متعدد الحدود ) هو توزيع احتمالي يصف احتمال حدوث عدة أحداث متنافية لعدد معين من المرات بعد عدة تجارب.

أي أنه إذا كانت التجربة العشوائية يمكن أن تؤدي إلى ثلاثة أحداث حصرية أو أكثر وكان احتمال حدوث كل حدث على حدة معروفًا، فسيتم استخدام التوزيع متعدد الحدود لحساب احتمال حدوث عدد معين من الأحداث عند إجراء تجارب متعددة. مرة في كل مرة.

وبالتالي فإن التوزيع متعدد الحدود هو تعميم للتوزيع ذي الحدين.

صيغة التوزيع متعددة الحدود

لحساب احتمال التوزيع متعدد الحدود، يجب عليك أولاً تحديد الحاصل بين مضروب إجمالي عدد البيانات ومضروب عدد تكرارات كل حدث، ويتم ضرب النتيجة في حاصل ضرب احتمالية كل حدث. جلبت إلى عدد تكرارات هذا الحدث.

بمعنى آخر، صيغة التوزيع متعدد الحدود هي كما يلي:

ذهب:

$P$

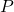
هو احتمال التوزيع متعدد الحدود المحسوب.
$n$

هو إجمالي عدد الاختبارات التي تم إجراؤها.
$x_i$

هو عدد مرات حدوث الحدث

$i$

.
$p_i$

هو احتمال وقوع الحدث

$i$

.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب احتمال وجود متغير يتبع التوزيع متعدد الحدود.

مثال التوزيع متعدد الحدود

للانتهاء من فهم مفهوم التوزيع متعدد الحدود، قمت أدناه بحل مثال لحساب احتمال التوزيع متعدد الحدود.

متجر يبيع ثلاثة منتجات مختلفة. عندما يقوم العميل بعملية شراء، فإن احتمال أن يكون المنتج أ أو المنتج ب أو المنتج ج هو 30% و15% و55% على التوالي. أوجد احتمال أنه عندما يبيع المتجر 8 وحدات، 2 من المنتج (أ)، وواحدة من المنتج (ب)، و5 من المنتج (ج).

تخضع المشكلة المحددة للتوزيع متعدد الحدود، لذلك من الضروري تطبيق الصيغة لهذا النوع من التوزيع الاحتمالي:

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

لذلك نقوم باستبدال البيانات من المشكلة في الصيغة وإجراء حساب الاحتمال:

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

لذا فإن احتمال حدوث ما يقوله بيان المشكلة هو 11.4%.

حاسبة التوزيع متعدد الحدود

اكتب عدد تكرارات كل حدث في المربع الأول، وبنفس الترتيب، احتمال وقوع كل حدث في المربع الثاني. ثم أدخل إجمالي عدد المحاولات التي تمت في آخر مساحة فارغة.

يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.

خصائص التوزيع متعدد الحدود

التوزيع متعدد الحدود له الخصائص التالية:

في التوزيع متعدد الحدود، القيمة المتوقعة لعدد مرات حدوث الحدث i عند إجراء تجارب n تساوي إجمالي عدد التجارب التي تم إجراؤها مضروبًا في احتمالية وقوع الحدث.

$E[x_i]=n\cdot p_i$

في التوزيع متعدد الحدود، يتم حساب التباين للحدث i باستخدام التعبير التالي:

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

وبالمثل، فإن التباين بين حدثين يعادل حاصل ضرب إجمالي عدد التجارب مضروبًا في احتمالية كل حدث مضروبًا في -1:

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

دالة توليد اللحظة للتوزيع متعدد الحدود هي:

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر