توزيع العينات نسبة
تشرح هذه المقالة ما هو توزيع العينات للنسبة في الإحصائيات. وبالمثل، ستجد صيغة توزيع العينات التناسبية، بالإضافة إلى تمرين تم حله خطوة بخطوة.
ما هو توزيع العينة لهذه النسبة؟
توزيع المعاينة للنسبة (أو توزيع المعاينة للنسب ) هو التوزيع الناتج عن حساب نسبة كل عينة محتملة من مجتمع ما. أي أن نسب المعاينة لجميع العينات الممكنة من مجتمع ما تشكل توزيع المعاينة لهذه النسبة.
بمعنى آخر، يتم الحصول على توزيع نسبة العينة من خلال دراسة جميع العينات التي يمكن اختيارها من مجتمع ما واستخلاص نسبة العينة من كل عينة. وبالتالي، فإن مجموعة نسب العينة المحسوبة تشكل توزيع العينة لهذه النسبة.
في حال كنت تتساءل عن الغرض من توزيع النسبة في المعاينة، يتم استخدامه في الإحصائيات لحساب احتمالية الاقتراب من قيمة نسبة السكان عند تحليل عينة واحدة.
صيغة توزيع العينات التناسبية
في الواقع، عندما ندرس نسبة من العينة، فإننا نقوم بتحليل حالات النجاح. ولذلك فإن المتغير العشوائي في الدراسة يتبع التوزيع الاحتمالي ذي الحدين .
وفقًا لنظرية الحد المركزي، بالنسبة للأحجام الكبيرة (n>30) يمكننا تقريب التوزيع ذي الحدين من التوزيع الطبيعي. ولذلك، فإن توزيع المعاينة للنسبة يقترب من التوزيع الطبيعي مع المعلمات التالية:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
ذهب
![]()
هو احتمال النجاح و
![]()
هو احتمال الفشل
![]()
.
ملاحظة: لا يمكن تقريب التوزيع ذي الحدين إلى التوزيع الطبيعي إلا إذا كان

![]()
و
![]()
.
لذلك، بما أن توزيع المعاينة للنسبة يمكن تقريبه إلى التوزيع الطبيعي، فإن صيغة حساب أي احتمال متعلق بنسبة العينة هي:

ذهب:
-

هي نسبة العينة
-

هي النسبة من السكان.
-

هو احتمال فشل السكان،

.
-

هو حجم العينة.
-

هو متغير يحدده التوزيع الطبيعي القياسي N(0,1).
مثال ملموس لتوزيع العينات التناسبية
بمجرد أن رأينا تعريف توزيع العينات المتناسبة وما هي الصيغ المرتبطة به، يتم تقديم مثال تم حله خطوة بخطوة أدناه لفهم المفهوم بشكل كامل.
- تشتري شركة صناعية دفعات من الأجزاء من مصنع يدعي أنه ينتج الأجزاء التي تحتوي على أجزاء معيبة بنسبة 3٪ فقط. للتحقق من ذلك، قررت الشركة تحليل طلبية مكونة من 500 قطعة. ما هو احتمال العثور على أكثر من 5% أجزاء معيبة في العينة؟
في هذه الحالة، نسبة السكان الذين نرغب في دراستهم هي 0.03، وبالتالي فإن المعلمة q تعادل 0.97.
![Rendered by QuickLaTeX.com \begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f4354c268853ec7b592bcacd23f3b214_l3.png)
لذلك، للعثور على الاحتمال الذي يطلبونه منا، يجب علينا حساب الإحصائية المقابلة من خلال تطبيق الصيغة التي رأيناها في القسم السابق:
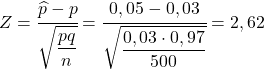
وبالتالي فإن احتمال الحصول على أكثر من 5% من الأجزاء المعيبة يعادل الاحتمال التالي:
![P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”></p>
</p>
<p style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-a5e5cff61f2cc97762df561b3e35a7ba_l3.png) أخيرًا، نبحث عن احتمال P[Z≤2.62] في جدول التوزيع Z ونحسب احتمال أن تطلب منا المشكلة:
أخيرًا، نبحث عن احتمال P[Z≤2.62] في جدول التوزيع Z ونحسب احتمال أن تطلب منا المشكلة:
![\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”></p>
</p>
<p style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-812f9b97c53e15da88b0cb7149f254c6_l3.png) في الختام، فإن احتمال العثور على أكثر من 5٪ أجزاء معيبة في العينة التي تم تحليلها هو 0.44٪.
في الختام، فإن احتمال العثور على أكثر من 5٪ أجزاء معيبة في العينة التي تم تحليلها هو 0.44٪.