توزيع ويبل

By دكتور بنيامين أندرسون زومار 3, 2023 احتمالا 0 Comments

تشرح هذه المقالة ما هو توزيع Weibull وفيم يتم استخدامه. بالإضافة إلى ذلك، ستتمكن من رؤية التمثيل البياني لتوزيع ويبل وما هي خصائص هذا النوع من التوزيع الاحتمالي.

ما هو توزيع ويبل؟

توزيع ويبل هو توزيع احتمالي مستمر يحدده معلمتان مميزتان: معلمة الشكل α ومعلمة المقياس α.

في الإحصاء، يستخدم توزيع ويبول بشكل رئيسي لتحليل البقاء على قيد الحياة. وبالمثل، فإن توزيعة ويبل لديها العديد من التطبيقات في مجالات مختلفة. سنتناول التفاصيل حول استخدام توزيع Weibull أدناه.

$X\sim\text{Weibull}(\alpha,\lambda)$

وفقًا للمؤلفين، يمكن أيضًا تحديد توزيع Weibull بثلاثة معلمات. بعد ذلك، تتم إضافة معلمة ثالثة تسمى قيمة العتبة، والتي تشير إلى الإحداثي الإحداثي الذي يبدأ عنده الرسم البياني للتوزيع.

تم تسمية توزيع وايبول على اسم السويدي والودي وايبول، الذي وصفه بالتفصيل في عام 1951. ومع ذلك، تم اكتشاف توزيع وايبول من قبل موريس فريشيه في عام 1927 وتم تطبيقه لأول مرة من قبل روزين وراملر في عام 1933.

رسم توزيع ويبل

بمجرد أن رأينا تعريف توزيع Weibull، سنرى كيف يختلف تمثيله الرسومي باختلاف قيم معلماته.

يمكنك أدناه رؤية عدة أمثلة لكيفية اختلاف الرسم البياني لوظيفة الكثافة لتوزيع Weibull اعتمادًا على قيمة معلمة الشكل ومعلمة المقياس.

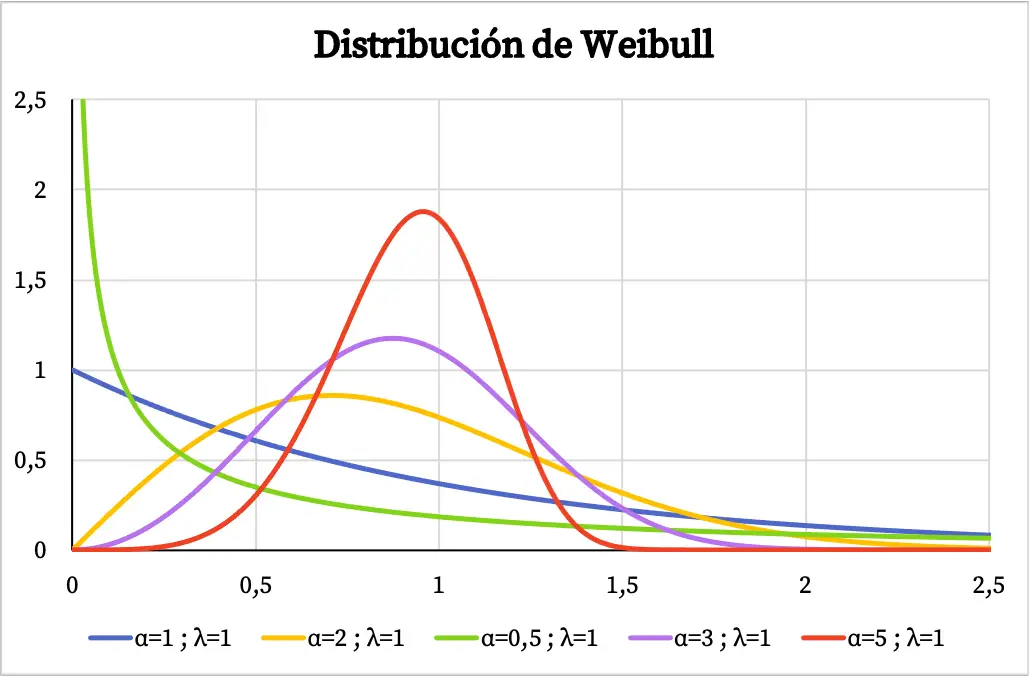
عند استخدام توزيع ويبل لنمذجة معدل فشل النظام كدالة للوقت، فإن قيمة معلمة الشكل α تعني ما يلي:

α<1: يتناقص معدل الفشل بمرور الوقت.
α=1: معدل الفشل ثابت مع مرور الوقت.
α>1: يزيد معدل الفشل بمرور الوقت.

من ناحية أخرى، في الرسم البياني التالي يمكنك رؤية دالة الاحتمالية التراكمية لتوزيع Weibull المرسومة بناءً على قيمها المميزة.

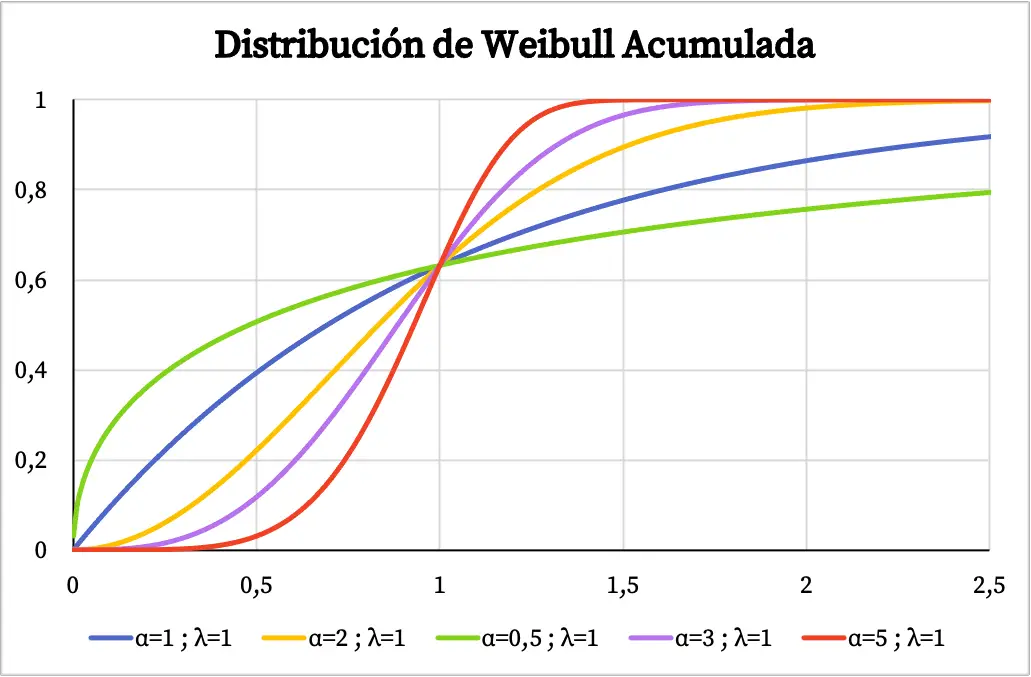
خصائص توزيع ويبل

يتميز توزيع Weibull بالخصائص التالية:

يحتوي توزيع Weibull على معلمتين مميزتين تحددان الرسم البياني الخاص به: معلمة الشكل α ومعلمة المقياس α. كلا المعلمتين أرقام حقيقية موجبة.

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p> </p> <ul style=$

توزيع Weibull يقبل فقط قيم الإحداثيات الإيجابية.

$x\in (0,+\infty)$

يتم حساب متوسط توزيع ويبل بالصيغة التالية:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

من ناحية أخرى، فإن صيغة إيجاد تباين توزيع ويبل هي:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

يمكن تحديد نمط المتغير العشوائي الذي يتبع توزيع Weibull مع α>1 بالتعبير التالي:

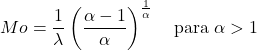
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”50″ width=”257″ style=”vertical-align: -17px;”></p> </p> <ul style=$

صيغة دالة الكثافة لتوزيع ويبل هي:

$\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

وبالمثل، فإن صيغة دالة الاحتمالية التراكمية لتوزيع ويبل هي:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

يتم حساب معامل عدم التماثل لتوزيع Weibull من خلال تطبيق الصيغة التالية:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

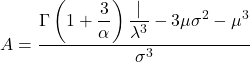
أخيرًا، الصيغة التي تجعل من الممكن تحديد معامل التفرطح لتوزيع ويبل هي التالية:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

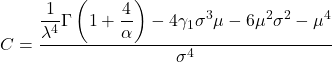
ذهب

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

تطبيقات توزيع ويبل

توزيعة ويبل لديها العديد من التطبيقات، بما في ذلك:

في الإحصاء التطبيقي، يتم استخدام توزيع ويبل في تحليل البقاء على قيد الحياة.
في الهندسة، يتم استخدام توزيع ويبل لنمذجة الوظائف المتعلقة بوقت التصنيع.
في أنظمة الرادار، لمحاكاة تشتت الإشارة المستقبلة.
في قطاع التأمين، لنموذج مدى المطالبات.
ففي علم الأرصاد الجوية، على سبيل المثال، لنمذجة ترددات سرعات الرياح المختلفة.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر