كيفية إجراء اختبار tukey-kramer post hoc في برنامج excel

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

الافتراضات المستخدمة في ANOVA هي كما يلي:

الفرضية الصفرية (H ₀ ): μ ₁ = μ ₂ = μ ₃ = … = μ _k (المتوسطات متساوية لكل مجموعة)

الفرضية البديلة: (Ha): تختلف إحدى الوسائل على الأقل عن غيرها

إذا كانت القيمة p لتحليل التباين (ANOVA) أقل من مستوى الأهمية، فيمكننا رفض فرضية العدم ونستنتج أن لدينا أدلة كافية لنقول أن إحدى وسائل المجموعة على الأقل تختلف عن الوسائل الأخرى.

ومع ذلك، هذا لا يخبرنا ما هي المجموعات التي تختلف عن بعضها البعض. وهذا يخبرنا ببساطة أنه ليست كل متوسطات المجموعة متساوية. من أجل معرفة المجموعات التي تختلف عن بعضها البعض بالضبط، نحتاج إلى إجراء اختبار لاحق.

الاختبار اللاحق الأكثر استخدامًا هو اختبار توكي-كرامر ، الذي يقارن المتوسط بين كل مجموعة زوجية من المجموعات.

يوضح المثال التالي كيفية إجراء اختبار Tukey-Kramer في Excel.

مثال: اختبار توكي-كرامر في إكسيل

لنفترض أننا أجرينا تحليل التباين أحادي الاتجاه على ثلاث مجموعات: A وB وC. نتائج تحليل التباين أحادي الاتجاه موضحة أدناه:

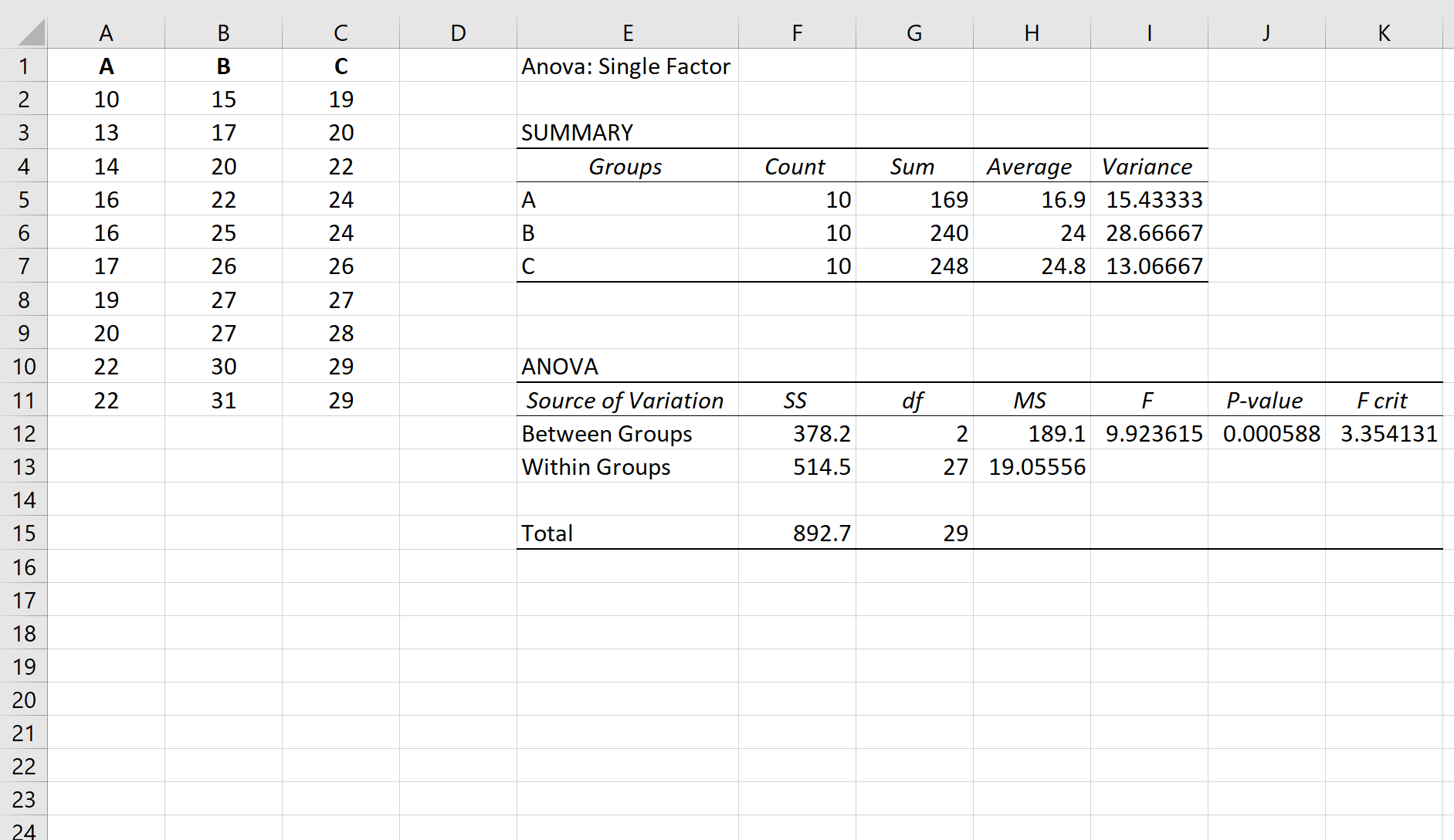
ذات صلة: كيفية إجراء ANOVA أحادي الاتجاه في Excel

القيمة p لجدول ANOVA هي 0.000588 . وبما أن هذه القيمة p أقل من 0.05، يمكننا رفض فرضية العدم ونستنتج أن المتوسطات بين المجموعات الثلاث غير متساوية.

لتحديد أي مجموعة من الوسائل المختلفة بالضبط، يمكننا إجراء اختبار توكي-كرامر اللاحق باستخدام الخطوات التالية:

الخطوة الأولى: أوجد الفرق المتوسط المطلق بين كل مجموعة.

أولاً، سنوجد فرق المتوسط المطلق بين كل مجموعة باستخدام المتوسطات المذكورة في الجدول الأول لنتيجة تحليل التباين:

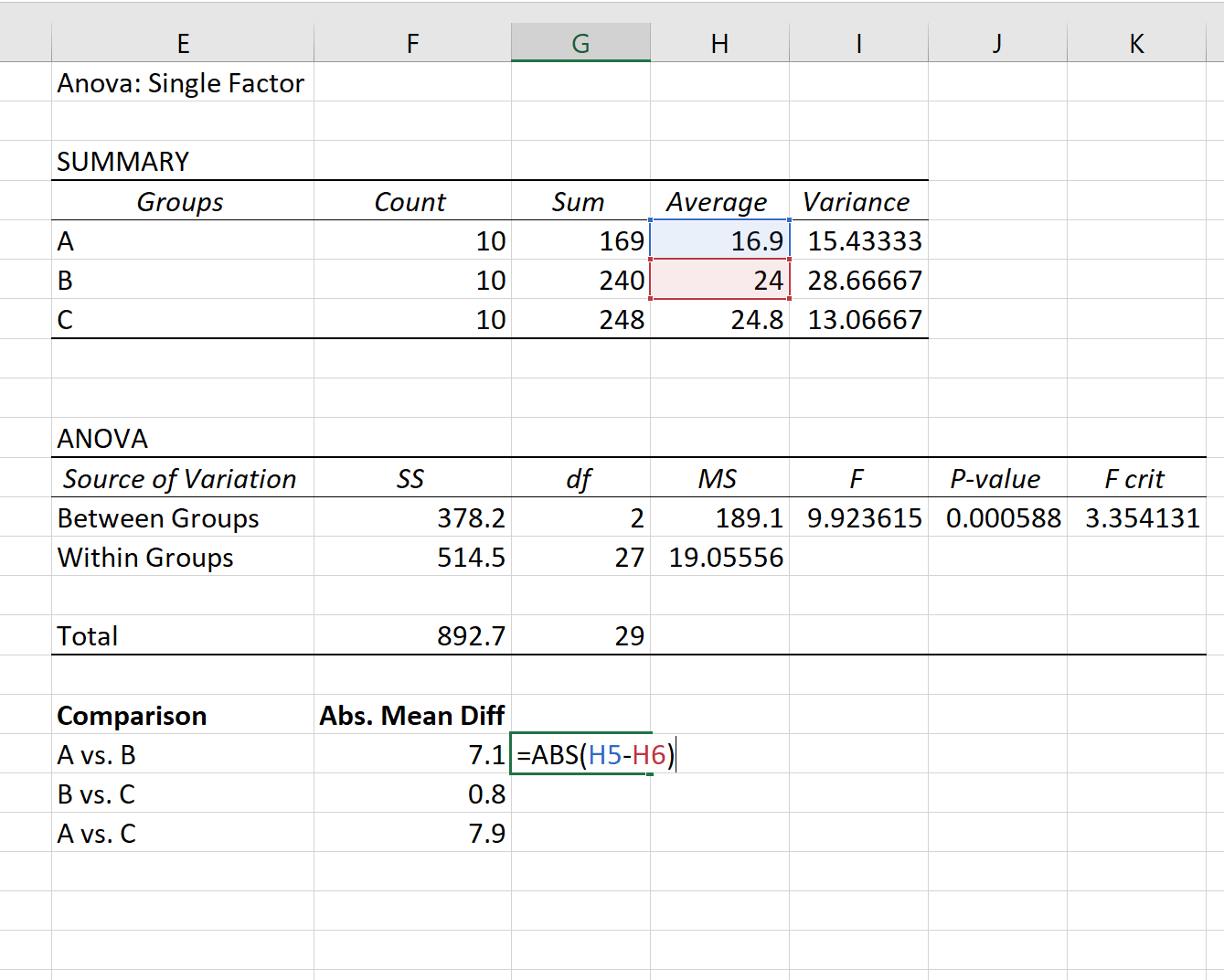
الخطوة 2: أوجد القيمة الحرجة لـ Q.

بعد ذلك، علينا إيجاد القيمة الحرجة لـ Q باستخدام الصيغة التالية:

القيمة الحرجة Q = Q*√(s ² _مجمعة / n.)

ذهب:

• Q = قيمة نطاق جدول الطالب Q
• s ² _مجمّع = التباين مجمّع عبر جميع المجموعات
• لا. = حجم العينة لمجموعة معينة

للعثور على قيمة Q، يمكنك الرجوع إلى جدول النطاق Q الذي يبدو كما يلي:

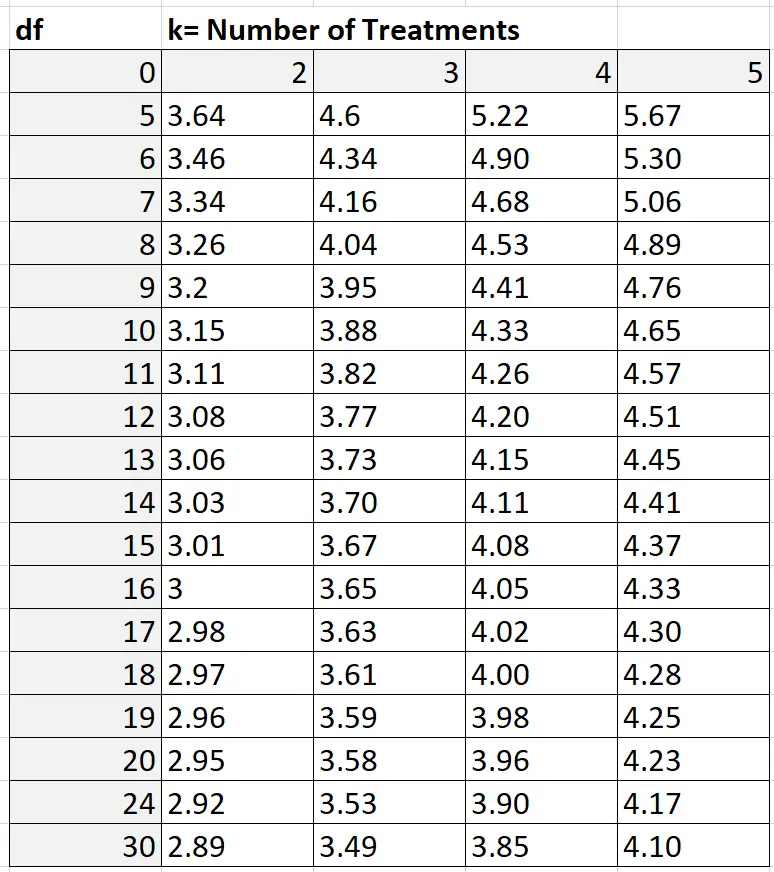
في مثالنا، k = عدد المجموعات، أي k = 3. يتم حساب درجات الحرية على النحو التالي: nk = 30 – 3 = 27. وبما أن 27 غير موضح في الجدول أعلاه، يمكننا استخدام تقدير متحفظ قدره 24 وبناء على k = 3 و df = 24 نجد أن Q = 3.53 .

يمكن حساب التباين المجمع كمتوسط تباينات المجموعات، والذي يتبين أنه 19.056 .

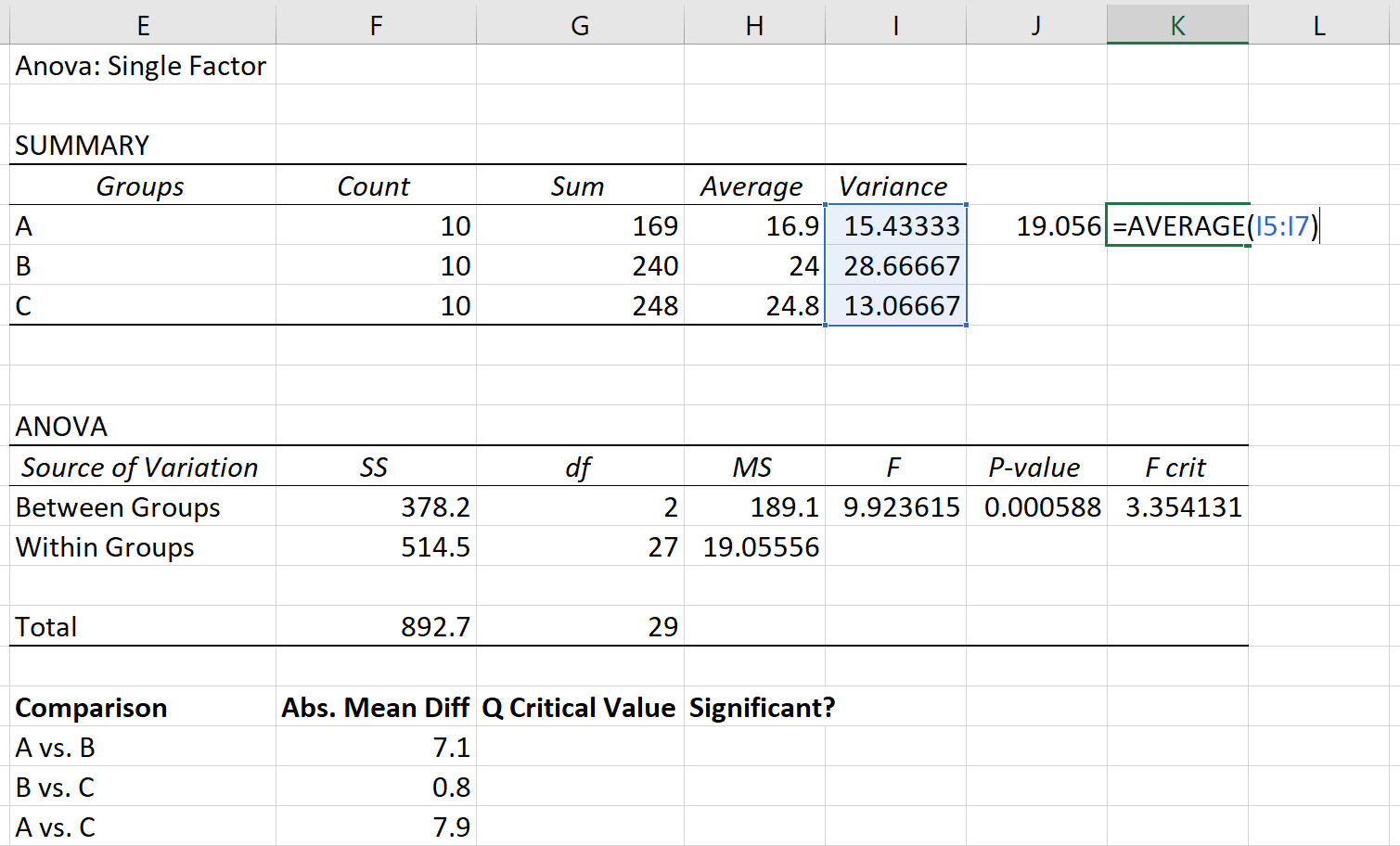
وأخيرا، حجم العينة لكل مجموعة هو 10.

وبالتالي، يمكن حساب القيمة الحرجة Q على النحو التالي:

القيمة الحرجة Q = Q*√(s ² _مجمعة / n.) = 3.53*√(19.056/10) = 4.87 .

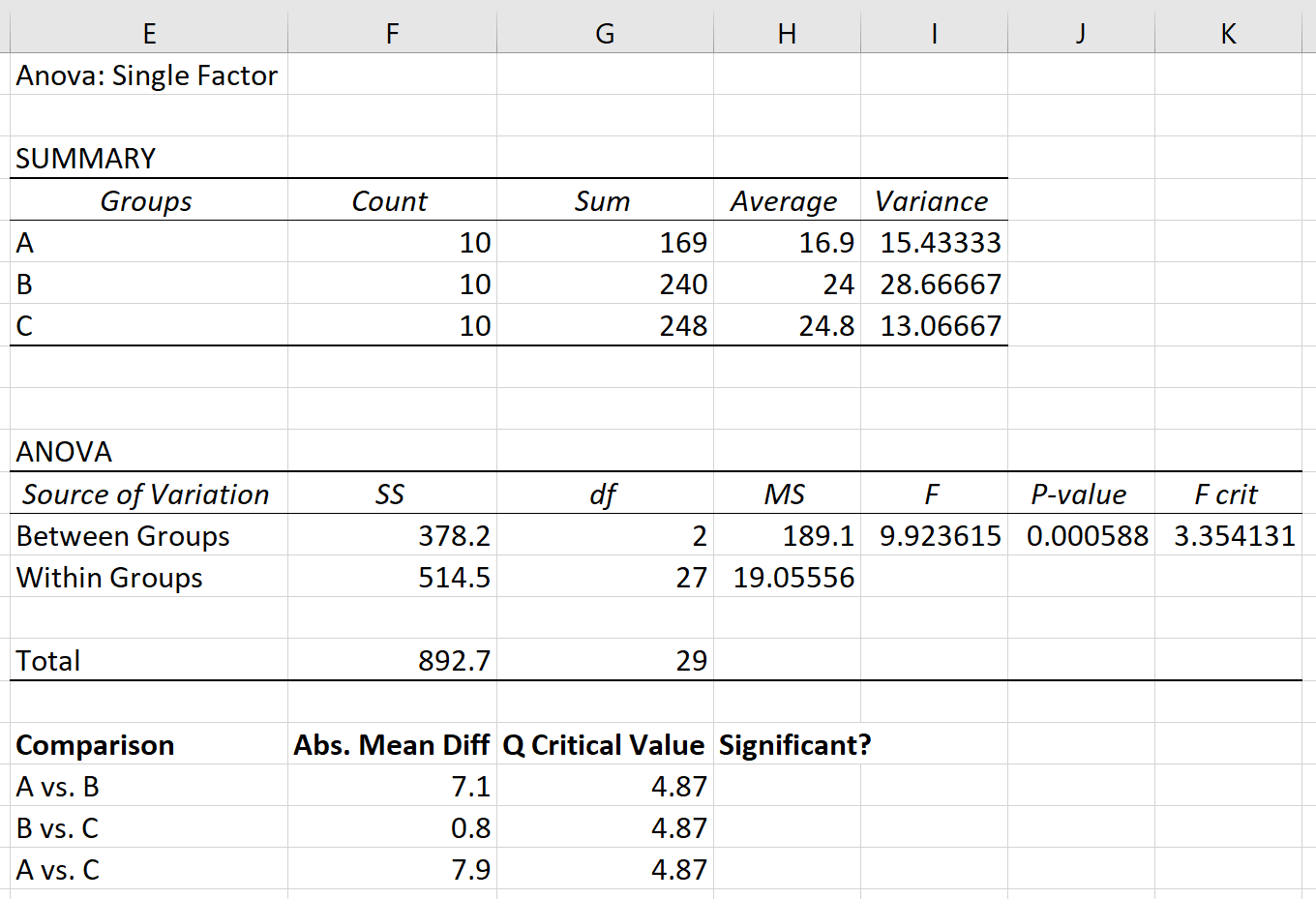
الخطوة 3: تحديد وسائل المجموعة المختلفة .

أخيرًا، يمكننا مقارنة فرق المتوسط المطلق بين كل مجموعة بالقيمة الحرجة Q. إذا كان فرق المتوسط المطلق أكبر من القيمة الحرجة Q، فإن الفرق بين متوسطات المجموعة يكون ذو دلالة إحصائية:

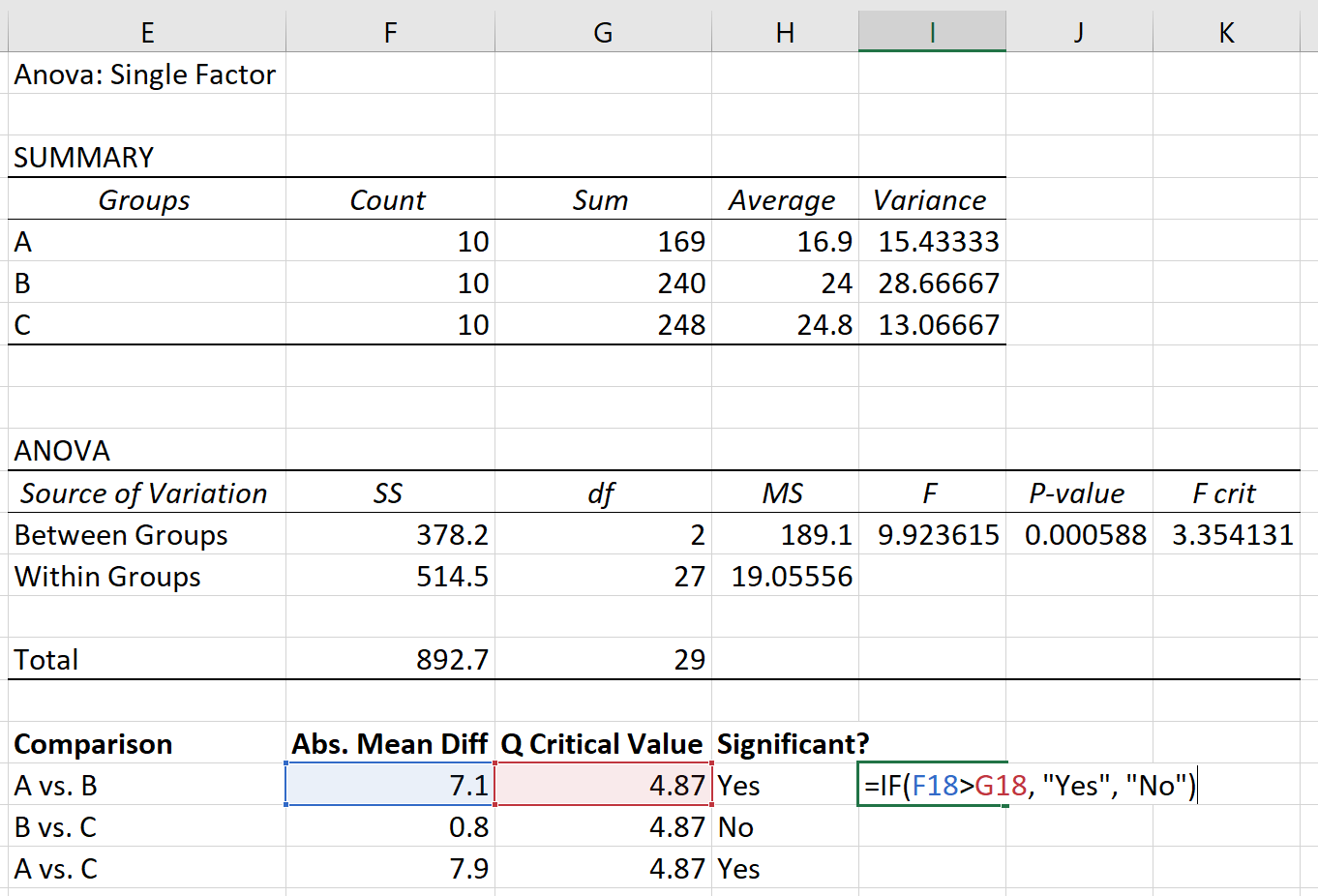
وبالاعتماد على اختبار توكي-كرامر اللاحق، وجدنا ما يلي:

• الفرق في المتوسطات بين المجموعة (أ) والمجموعة (ب) له دلالة إحصائية.
• الفرق في المتوسطات بين المجموعة B والمجموعة C ليس ذو دلالة إحصائية.
• الفرق في المتوسطات بين المجموعة (أ) والمجموعة (ج) له دلالة إحصائية.

مصادر إضافية

كيفية إجراء ANOVA أحادي الاتجاه في Excel
دليل لاستخدام اختبار ما بعد المخصص مع ANOVA