جودة الملاءمة
تشرح هذه المقالة مدى جودة الملاءمة في الإحصائيات. وبالمثل، فهو يوضح كيفية قياس جودة الملاءمة لنموذج الانحدار، وبالإضافة إلى ذلك، ستتمكن من رؤية تمرين تم حله حول جودة الملاءمة.
ما هو حسن اللياقة؟
في الإحصائيات، جودة الملاءمة هي مدى ملاءمة نموذج الانحدار لعينة البيانات. بمعنى آخر، تشير جودة ملاءمة نموذج الانحدار إلى مستوى الاقتران بين مجموعة الملاحظات والقيم التي تم الحصول عليها من خلال الانحدار.
لذلك، كلما كانت جودة ملاءمة نموذج الانحدار أفضل، كلما كان تفسيره للبيانات قيد الدراسة أفضل. وبالتالي، نريد أن يكون النموذج الإحصائي مناسبًا بشكل أفضل، كلما كان ذلك أفضل.
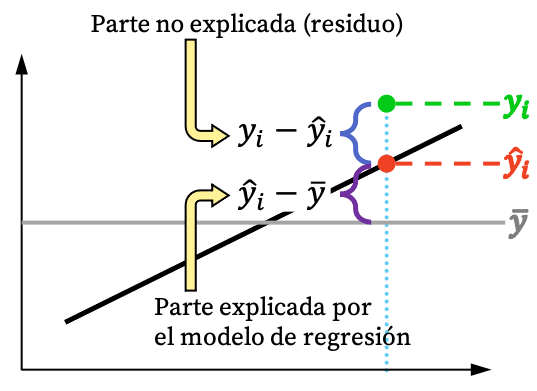
كما ترون من الصورة أعلاه، عادة لا يمكن تفسير قيمة الملاحظة بشكل كامل من خلال نموذج الانحدار. ولكن من الناحية المنطقية، كلما استطاع نموذج الانحدار أن يشرح من مجموعة البيانات، كلما كان النموذج مناسبًا بشكل أفضل. باختصار، نحن مهتمون بنموذج انحداري يكون محكمًا قدر الإمكان.
مدى ملاءمة نموذج الانحدار
لتحديد مدى ملاءمة نموذج الانحدار، يستخدم المرء عادة معامل التحديد ، وهو معامل إحصائي يشير إلى النسبة المئوية التي يفسرها نموذج الانحدار. وبالتالي، كلما ارتفع معامل تحديد النموذج، كلما كان تكييف النموذج أفضل مع عينة البيانات.
ومع ذلك، تجدر الإشارة إلى أنه كلما زاد عدد المتغيرات في نموذج الانحدار، كلما ارتفع معامل التحديد الخاص به. لهذا السبب، غالبًا ما يستخدم معامل التحديد المعدل أيضًا لقياس مدى ملاءمة النموذج. ومعامل التحديد المعدل هو اختلاف عن المعامل السابق الذي يشير إلى النسبة المئوية الموضحة بنموذج الانحدار، مع معاقبة كل متغير توضيحي مدرج في النموذج.
ولذلك يفضل استخدام معامل التحديد المعدل لمقارنة نموذجين بعدد من المتغيرات المختلفة، لأنه يأخذ في الاعتبار عدد المتغيرات التي يتضمنها النموذج.
أخيرًا، تجدر الإشارة إلى أنه يمكن أيضًا استخدام اختبار Chi-square لقياس مدى ملاءمة نموذج الانحدار، على الرغم من استخدام قيم المعاملين السابقين عادةً.
مثال ملموس على حسن النية
وأخيرا، سوف نرى تمرينا محلولا في نوعية التكيف للانتهاء من استيعاب هذا المفهوم الإحصائي.
- وبنفس سلسلة البيانات، يتم تنفيذ نموذجين مختلفين للانحدار الخطي، ويمكنك رؤية نتائجهما في الجدول التالي. ما هو النموذج الأفضل للاستخدام؟
| نموذج الانحدار 1 | نموذج الانحدار 2 | |
|---|---|---|
| معامل التحديد | 57% | 64% |
| معامل التحديد المعدل | 49% | 43% |
| عدد المتغيرات التوضيحية | 3 | 7 |
في هذه الحالة، نفترض أن كلا النموذجين يستوفيان الافتراضات السابقة لنماذج الانحدار الخطي، وبالتالي، نحتاج فقط إلى تحليل مدى ملاءمة النماذج.
يحتوي نموذج الانحدار 2 على معامل تحديد أعلى من نموذج الانحدار 1، لذلك يبدو من البديهي أن يكون نموذج انحدار أفضل لأنه قادر على شرح عينة البيانات بشكل أفضل.
ومع ذلك، يحتوي نموذج الانحدار 2 على 7 متغيرات مستقلة في النموذج، في حين أن نموذج الانحدار 1 يحتوي على 3 متغيرات فقط. لذلك سيكون النموذج 2 أكثر تعقيدًا وأصعب في التفسير من النموذج الأول.
بالإضافة إلى ذلك، إذا نظرنا إلى معامل التحديد المعدل، والذي يأخذ في الاعتبار عدد المتغيرات في النموذج، فإن نموذج الانحدار 1 لديه معامل تحديد معدل أعلى من نموذج الانحدار 2.
في الختام، على الرغم من أنه من الأفضل استخدام نموذج الانحدار 1، نظرًا لأن معامل التحديد المعدل الخاص به أعلى من معامل التحديد المعدل 2. يحتوي نموذج الانحدار 2 على معامل تحديد غير معدل أعلى، وذلك لأنه يتضمن العديد من المتغيرات في الانحدار النموذج 1. النموذج، الذي يزيد من قيمة المعامل المذكور ولكنه يجعل تفسير النموذج أكثر صعوبة، وبالتأكيد، يجعل التنبؤ بقيمة جديدة أسوأ.
لمقارنة النماذج بأعداد مختلفة من المتغيرات، فمن الأفضل استخدام معامل التحديد المعدل لأنه يعاقب على كل متغير يضاف إلى النموذج. كما رأيت في هذا المثال، وفقًا لمعامل التحديد غير المعدل، فإن نموذج الانحدار 2 هو الأفضل، ومع ذلك، من خلال معامل التحديد المعدل يمكننا معرفة أن نموذج الانحدار 1 هو في الواقع أفضل.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر