ما الذي يعتبر قطعة أرض متبقية جيدة أو سيئة؟

في تحليل الانحدار، الرسم المتبقي هو نوع من الرسم الذي يعرض القيم المجهزة لنموذج الانحدار على المحور السيني وبقايا النموذج على طول المحور الصادي.

عند الفحص البصري للتخطيط المتبقي، فإننا نبحث عمومًا عن شيئين لتحديد ما إذا كان التخطيط “جيدًا” أو “سيئًا”:

1. هل تظهر البقايا اتجاها واضحا؟

• في قطعة الأرض المتبقية “الجيدة”، لا تظهر البقايا أي اتجاه واضح.
• في المخطط المتبقي “السيئ”، يكون للمخلفات نوع من النمط مثل المنحنى أو الموجة. يشير هذا إلى أن نموذج الانحدار الذي استخدمناه لا يوفر ملاءمة مناسبة للبيانات.

2. هل تزيد البواقي أم تنقص في التباين بشكل منتظم؟

• في المخطط المتبقي “الجيد”، يتم توزيع البقايا بشكل عشوائي حول الصفر دون زيادة أو نقصان منهجي في التباين.
• في المخطط المتبقي “السيئ”، يزيد تباين البقايا أو ينقص بشكل منهجي.

إذا تم تصنيف قطعة الأرض المتبقية على أنها “جيدة”، فهذا يعني أنه يمكننا الوثوق بنتائج نموذج الانحدار وأنه من الآمن تفسير معاملات النموذج.

ومع ذلك، إذا تم تصنيف قطعة الأرض المتبقية على أنها “سيئة”، فهذا يعني أن نتائج النموذج غير موثوقة ونحن بحاجة إلى ملاءمة نموذج انحدار مختلف مع البيانات.

تشرح الأمثلة التالية كيفية تفسير المخططات المتبقية “الجيدة” و”السيئة” في الممارسة العملية.

مثال 1: أثر متبقي “جيد”.

لنفترض أننا نلائم نموذج الانحدار وحصلنا على المخطط المتبقي التالي:

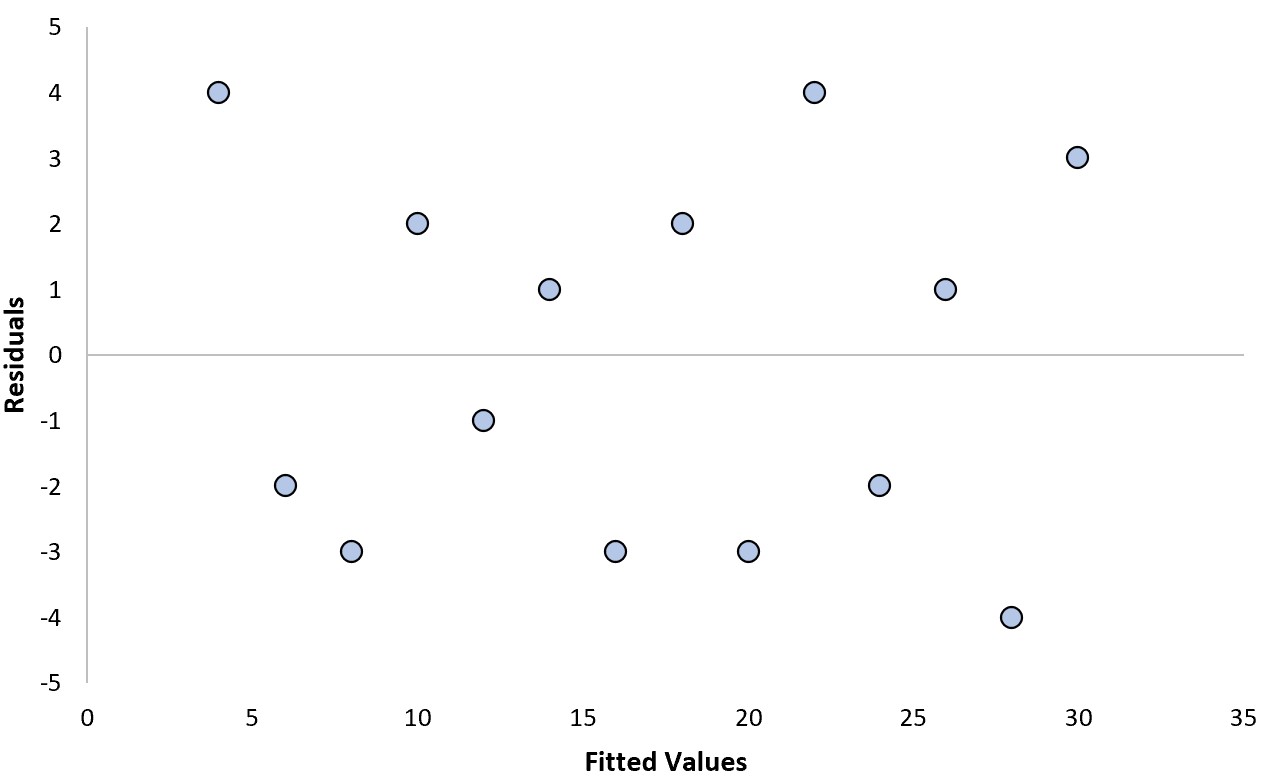
يمكننا الإجابة على السؤالين التاليين لتحديد ما إذا كانت هذه قطعة أرض متبقية “جيدة”:

1. هل تظهر البقايا اتجاها واضحا؟

كلا، البقايا متناثرة بشكل عشوائي حول الصفر، بدون نمط واضح.

2. هل تزيد البواقي أم تنقص في التباين بشكل منتظم؟

لا، فالبقايا لها تباين ثابت إلى حد ما (أي المسافة بين البقايا والقيمة الصفرية) عند كل مستوى من القيم المجهزة.

وبما أننا أجبنا بـ “لا” على هذين السؤالين، فإننا نعتبر هذه قطعة أرض “جيدة” متبقية.

ولذلك يمكننا الوثوق بنتائج نموذج الانحدار وتفسير معاملات النموذج بشكل آمن.

المثال 2: قطعة أرض متبقية “سيئة” بنموذج واضح

لنفترض أننا نلائم نموذج الانحدار وحصلنا على المخطط المتبقي التالي:

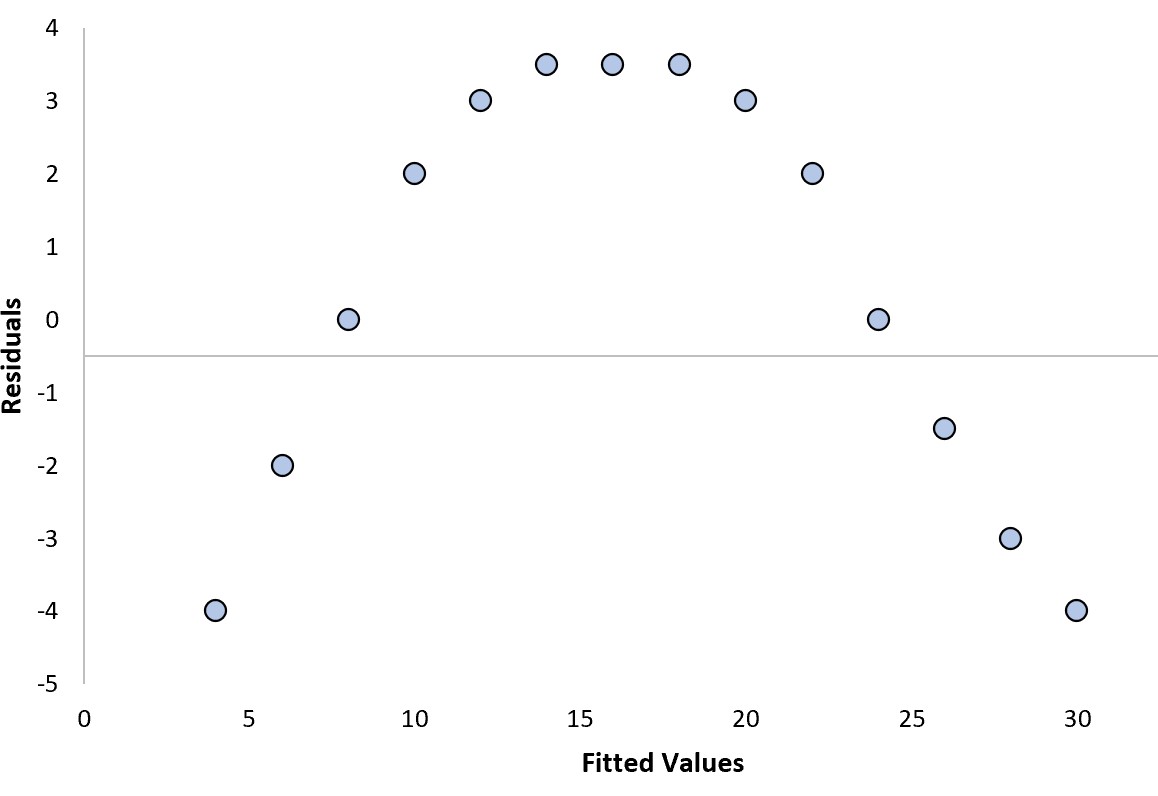
يمكننا الإجابة على السؤالين التاليين لتحديد ما إذا كانت هذه قطعة أرض متبقية “جيدة”:

1. هل تظهر البقايا اتجاها واضحا؟

نعم . تظهر البقايا نمطًا منحنيًا.

2. هل تزيد البواقي أم تنقص في التباين بشكل منتظم؟

نعم . تحتوي البقايا على مستويات مختلفة من التباين عند مستويات مختلفة من القيم المجهزة.

وبما أننا أجبنا بـ “نعم” على واحد على الأقل من هذه الأسئلة، فإننا نعتبر هذه مؤامرة متبقية “سيئة”.

وهذا يعني أن نموذج الانحدار لا يوفر ملاءمة جيدة للبيانات.

على وجه الخصوص، يشير النمط المنحني في المخطط المتبقي إلى أن نموذج الانحدار الخطي يفشل في ملاءمة البيانات وأن نموذج الانحدار التربيعي من المرجح أن يقوم بعمل أفضل.

مثال 3: مؤامرة متبقية “سيئة” مع تباين متزايد

لنفترض أننا نلائم نموذج الانحدار وحصلنا على المخطط المتبقي التالي:

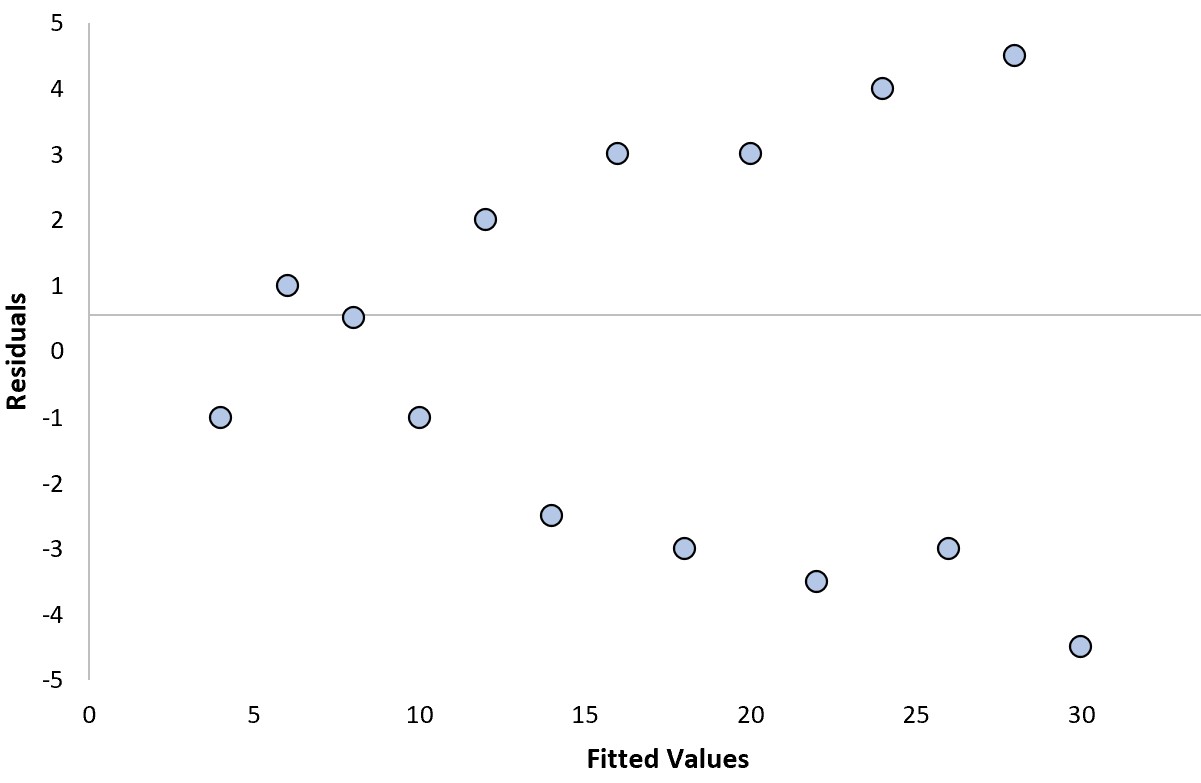
يمكننا الإجابة على السؤالين التاليين لتحديد ما إذا كانت هذه قطعة أرض متبقية “جيدة”:

1. هل تظهر البقايا اتجاها واضحا؟

لا، لا يوجد اتجاه واضح في المخلفات.

2. هل تزيد البواقي أم تنقص في التباين بشكل منتظم؟

نعم . ويزداد تباين البقايا مع زيادة القيم المجهزة.

وبما أننا أجبنا بـ “نعم” على واحد على الأقل من هذه الأسئلة، فإننا نعتبر هذه مؤامرة متبقية “سيئة”.

في هذا المثال بالذات، تعاني البقايا من التغايرية ، والتي تشير إلى التباين غير المتكافئ للبواقي عند مستويات مختلفة من القيم المجهزة.

وهذا يعني أن نتائج نموذج الانحدار قد لا تكون موثوقة.

ارجع إلى هذه المقالة للتعرف على طرق مختلفة لحل مشكلة عدم التجانس في نموذج الانحدار.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إنشاء قطع أرض متبقية باستخدام برامج إحصائية مختلفة:

كيفية إنشاء قطعة أرض متبقية في R
كيفية إنشاء مؤامرة المتبقية في بيثون
كيفية إنشاء مؤامرة المتبقية في إكسيل
كيفية إنشاء قطعة أرض متبقية في SAS