كيفية إنشاء وتفسير منحنى roc في stata
الانحدار اللوجستي هو طريقة إحصائية نستخدمها لتناسب نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا. لتقييم مدى ملاءمة نموذج الانحدار اللوجستي لمجموعة البيانات، يمكننا النظر إلى المقياسين التاليين:
- الحساسية: احتمال أن يتنبأ النموذج بنتيجة إيجابية لملاحظة ما عندما تكون النتيجة إيجابية بالفعل.
- الخصوصية: احتمال أن يتنبأ النموذج بنتيجة سلبية لملاحظة ما عندما تكون النتيجة سلبية بالفعل.
إحدى الطرق البسيطة لتصور هذين المقياسين هي إنشاء منحنى ROC ، وهو رسم بياني يعرض حساسية وخصوصية نموذج الانحدار اللوجستي.
يشرح هذا البرنامج التعليمي كيفية إنشاء وتفسير منحنى ROC في Stata.
مثال: منحنى ROC في Stata
في هذا المثال، سنستخدم مجموعة بيانات تسمى lbw ، والتي تحتوي على المتغيرات التالية لـ 189 أمًا:
- منخفض – ما إذا كان وزن الطفل منخفضًا عند الولادة أم لا. 1 = نعم، 0 = لا.
- العمر – عمر الأم.
- الدخان – سواء كانت الأم تدخن أثناء الحمل أم لا. 1 = نعم، 0 = لا.
سوف نلائم نموذج الانحدار اللوجستي مع البيانات باستخدام العمر والتدخين كمتغيرات توضيحية وانخفاض الوزن عند الولادة كمتغير الاستجابة. بعد ذلك، سنقوم بإنشاء منحنى ROC لتحليل مدى ملاءمة النموذج للبيانات.
الخطوة 1: تحميل وعرض البيانات.
قم بتحميل البيانات باستخدام الأمر التالي:
استخدم https://www.stata-press.com/data/r13/lbw
احصل على فهم سريع لمجموعة البيانات باستخدام الأمر التالي:
كي تختصر
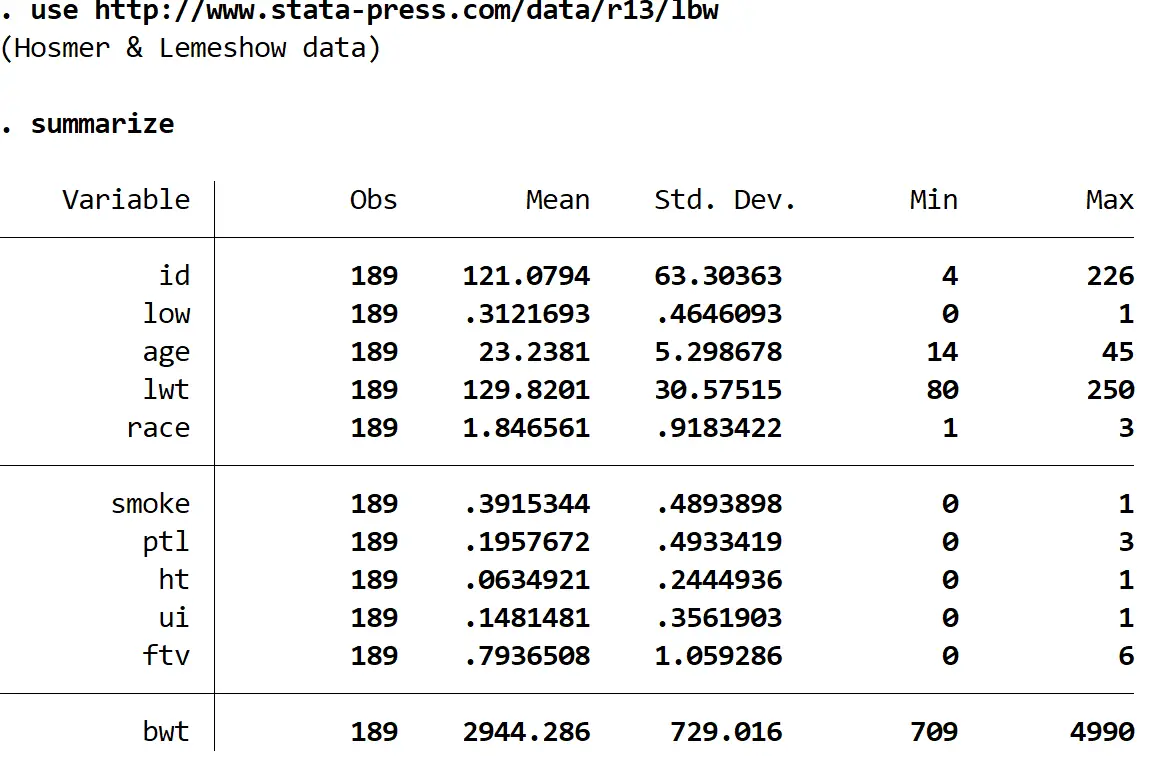
هناك 11 متغيرًا مختلفًا في مجموعة البيانات، لكن الثلاثة الوحيدة التي نهتم بها هي المستوى المنخفض والعمر والتدخين.
الخطوة 2: ملاءمة نموذج الانحدار اللوجستي.
استخدم الأمر التالي لملاءمة نموذج الانحدار اللوجستي:
سجل الدخان منخفض العمر
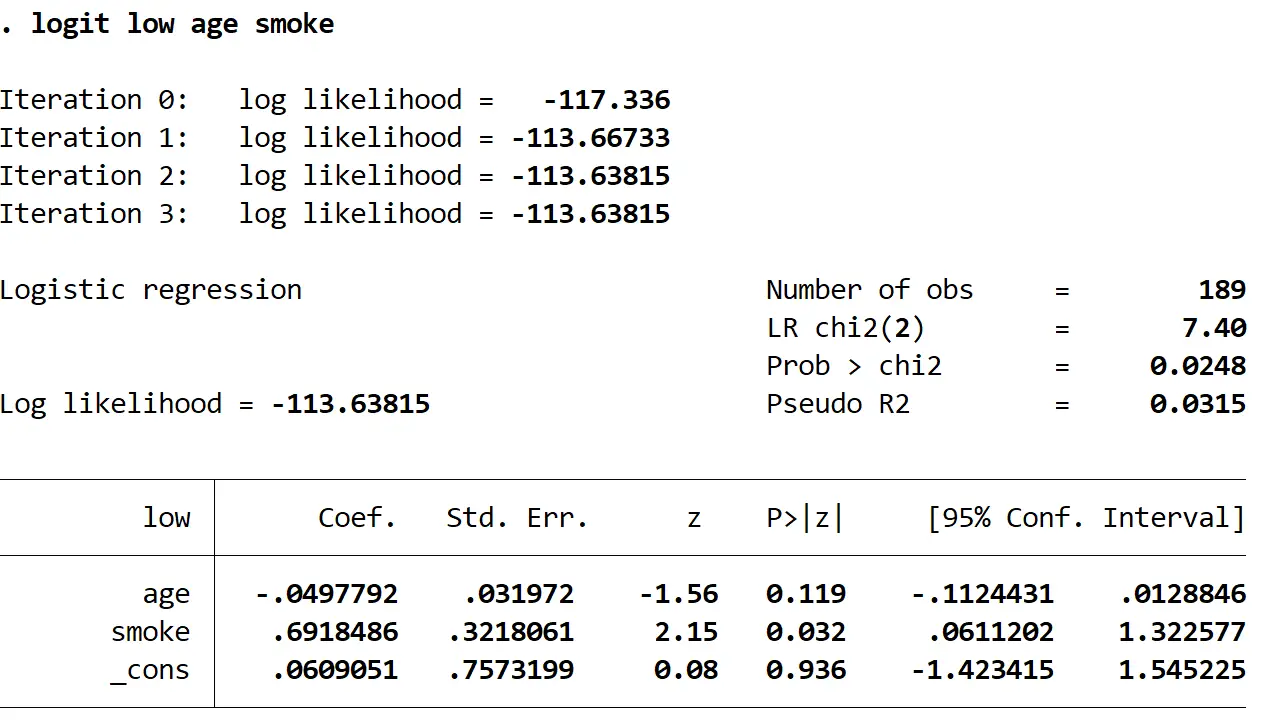
الخطوة 3: إنشاء منحنى ROC.
يمكننا إنشاء منحنى ROC للنموذج باستخدام الأمر التالي:
lroc
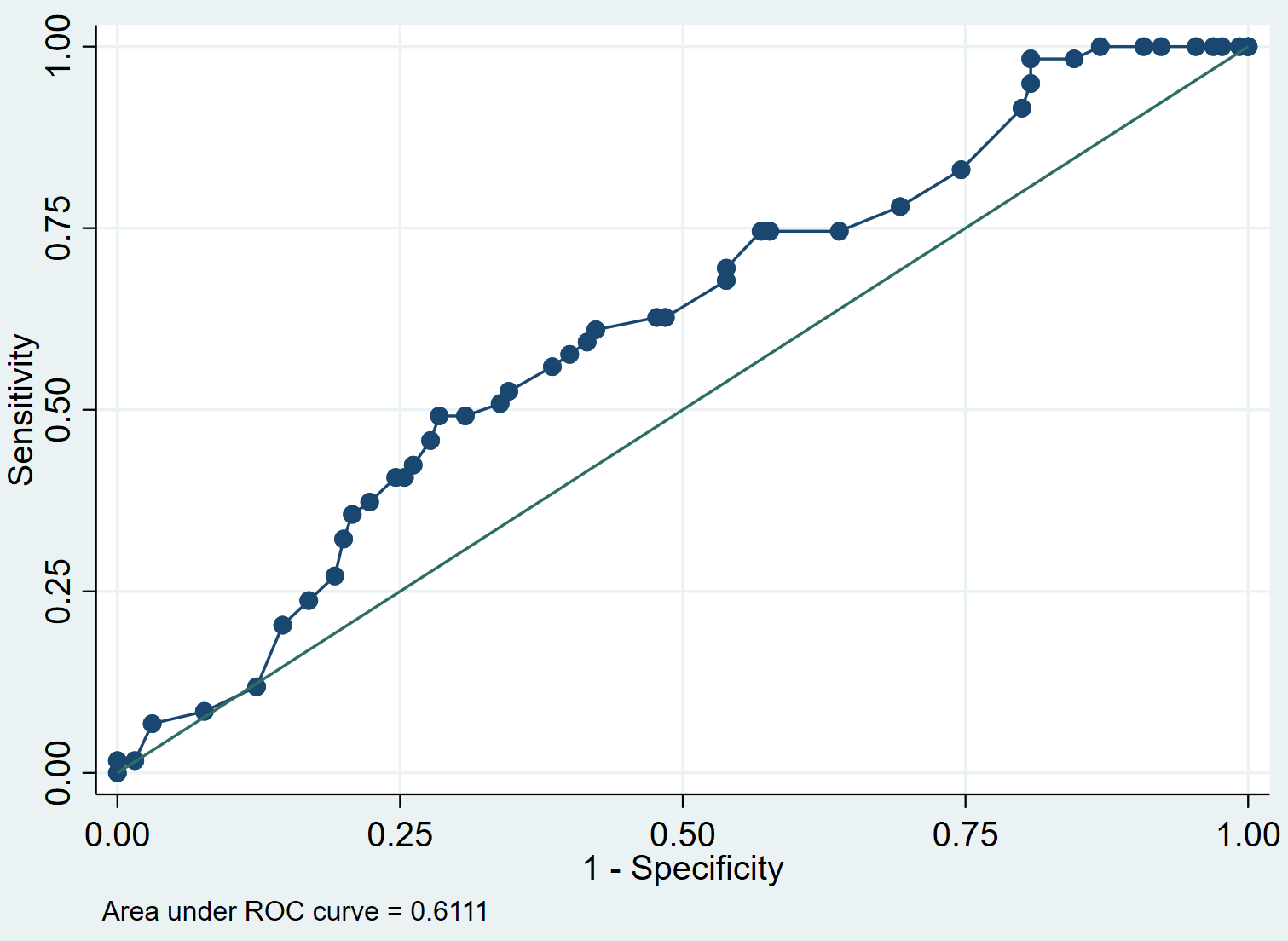
الخطوة 4: تفسير منحنى ROC.
عندما نلائم نموذج الانحدار اللوجستي، يمكن استخدامه لحساب احتمالية أن يكون لملاحظة معينة نتيجة إيجابية، بناءً على قيم متغيرات التوقع.
لتحديد ما إذا كان ينبغي تصنيف الملاحظة على أنها إيجابية، يمكننا اختيار عتبة بحيث يتم تصنيف الملاحظات ذات الاحتمال المعدل فوق العتبة على أنها إيجابية ويتم تصنيف جميع الملاحظات ذات الاحتمال المعدل أقل من العتبة على أنها سلبية. .
على سبيل المثال، لنفترض أننا اخترنا عتبة قدرها 0.5. وهذا يعني أن أي ملاحظة ذات احتمال معدل أكبر من 0.5 ستكون لها نتيجة إيجابية، في حين أن أي ملاحظة ذات احتمال معدل أقل من أو يساوي 0.5 ستكون لها نتيجة سلبية.
يوضح لنا منحنى ROC قيم الحساسية مقابل الخصوصية 1 حيث تتغير قيمة العتبة من 0 إلى 1. النموذج ذو الحساسية العالية والخصوصية سيكون له منحنى ROC يعانق الزاوية اليسرى العليا من المخطط. سيكون للنموذج ذو الحساسية المنخفضة والخصوصية المنخفضة منحنى قريب من قطري 45 درجة.
تعطينا AUC (المنطقة أسفل المنحنى) فكرة عن قدرة النموذج على التمييز بين النتائج الإيجابية والسلبية. يمكن أن تتراوح المساحة تحت المنحنى من 0 إلى 1. وكلما ارتفعت المساحة تحت المنحنى، كان النموذج أفضل في تصنيف النتائج بشكل صحيح. في مثالنا، يمكننا أن نرى أن AUC هو 0.6111 .
يمكننا استخدام AUC لمقارنة أداء نموذجين أو أكثر. النموذج ذو أعلى AUC يحقق أفضل أداء.
مصادر إضافية
كيفية إجراء الانحدار اللوجستي في ستاتا
كيفية تفسير منحنى ROC وAUC لنموذج الانحدار اللوجستي