حجم التأثير: ما هو ولماذا يهم
“إن الأهمية الإحصائية هي الشيء الأقل إثارة للاهتمام في النتائج. أنت بحاجة إلى وصف النتائج من حيث مقاييس الحجم – ليس فقط تأثير العلاج على الأشخاص، ولكن مدى تأثيره عليهم. -الجين الخامس. الزجاج
في الإحصاء، غالبًا ما نستخدم القيم الاحتمالية لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين مجموعتين.
على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كانت طريقتان مختلفتان للدراسة تؤديان إلى درجات اختبار مختلفة. إذن، لدينا مجموعة مكونة من 20 طالبًا يستخدمون أسلوب دراسة واحدًا للتحضير للاختبار بينما تستخدم مجموعة أخرى مكونة من 20 طالبًا أسلوب دراسة مختلفًا. ثم نعطي كل طالب نفس الاختبار.
وبعد إجراء اختبار t لعينتين لتحديد الفرق في المتوسطات، نجد أن القيمة p للاختبار هي 0.001. وإذا استخدمنا مستوى دلالة 0.05 فهذا يعني أن هناك فرقاً ذا دلالة إحصائية بين متوسطي نتائج المجموعتين. لذا فإن أسلوب الدراسة له تأثير على نتائج الاختبار.
ومع ذلك، في حين أن القيمة p تخبرنا أن أسلوب الدراسة له تأثير على درجات الاختبار، إلا أنها لا تخبرنا بحجم هذا التأثير. ولكي نفهم ذلك، علينا أن نعرف حجم التأثير .
ما هو حجم التأثير؟
حجم التأثير هو وسيلة لقياس الفرق بين مجموعتين.
في حين أن القيمة الاحتمالية يمكن أن تخبرنا ما إذا كان هناك فرق ذو دلالة إحصائية بين مجموعتين أم لا، فإن حجم التأثير يمكن أن يخبرنا عن مدى حجم هذا الاختلاف حقًا. من الناحية العملية، تعتبر أحجام التأثير أكثر إثارة للاهتمام ومفيدة في معرفتها من القيم الاحتمالية.
هناك ثلاث طرق لقياس حجم التأثير، اعتمادًا على نوع التحليل الذي تقوم به:
1. فرق المتوسط الموحد
عندما تريد دراسة فرق المتوسط بين مجموعتين، فإن الطريقة المناسبة لحساب حجم التأثير هي استخدام فرق متوسط موحد . تُعرف الصيغة الأكثر شيوعًا المستخدمة باسم Cohen’s d ، والتي يتم حسابها على النحو التالي:
د كوهين = ( x1 – x2 ) / ث
حيث x 1 و x 2 هما متوسطي العينة للمجموعة 1 والمجموعة 2، على التوالي، و s هو الانحراف المعياري للمجتمع الذي تم سحب المجموعتين منه.
باستخدام هذه الصيغة، من السهل تفسير حجم التأثير:
- يشير d d 1 إلى أن متوسطي المجموعتين يختلفان بانحراف معياري واحد.
- يعني d 2 أن متوسطات المجموعة تختلف بانحرافين معياريين.
- ويشير d 2.5 إلى أن الوسيطين يختلفان بمقدار 2.5 انحراف معياري، وهكذا.
هناك طريقة أخرى لتفسير حجم التأثير وهي: حجم التأثير 0.3 يعني أن درجة الشخص العادي في المجموعة 2 هي 0.3 انحرافات معيارية أعلى من متوسط الشخص في المجموعة 1 وبالتالي تتجاوز درجات 62٪ من درجات المجموعة 1 . .
يوضح الجدول التالي أحجام التأثيرات المختلفة والنسب المئوية المقابلة لها:
| حجم التأثير | النسبة المئوية للمجموعة 2 التي ستكون أقل من متوسط الأشخاص في المجموعة 1 |
|---|---|
| 0.0 | 50% |
| 0.2 | 58% |
| 0.4 | 66% |
| 0.6 | 73% |
| 0.8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99.9% |
كلما زاد حجم التأثير، زاد الفرق بين الفرد العادي في كل مجموعة.
بشكل عام، يعتبر d الذي يبلغ 0.2 أو أقل حجم تأثير صغير، ويعتبر d الذي يبلغ حوالي 0.5 حجم تأثير متوسط، ويعتبر d الذي يبلغ 0.8 أو أكبر حجم تأثير كبيرًا.
لذلك، إذا لم يختلف متوسط مجموعتين بمقدار 0.2 انحراف معياري على الأقل، يكون الفرق غير مهم، حتى لو كانت القيمة p ذات دلالة إحصائية.
2. معامل الارتباط
عندما تريد دراسة العلاقة الكمية بين متغيرين، فإن الطريقة الأكثر شيوعًا لحساب حجم التأثير هي استخدام معامل ارتباط بيرسون . وهو مقياس للارتباط الخطي بين متغيرين X و Y. وله قيمة تتراوح بين -1 و1 حيث:
- يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
- يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
- يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين
صيغة حساب معامل ارتباط بيرسون معقدة للغاية، ولكن يمكن العثور عليها هنا لأولئك المهتمين.
كلما زاد معامل الارتباط عن الصفر، كلما كانت العلاقة الخطية بين متغيرين أقوى. ويمكن ملاحظة ذلك أيضًا من خلال إنشاء مخطط تشتت بسيط لقيم المتغيرين X و Y.
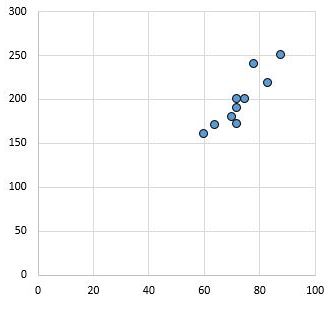
على سبيل المثال، يوضح مخطط التشتت التالي قيم متغيرين مع معامل ارتباط r = 0.94.
وهذه القيمة بعيدة عن الصفر، مما يدل على وجود علاقة إيجابية قوية بين المتغيرين.
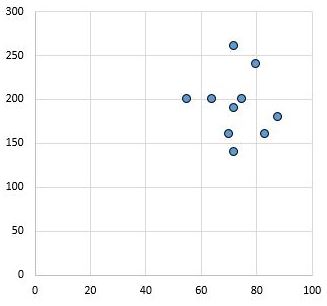
وعلى العكس من ذلك، يوضح مخطط التشتت التالي قيم متغيرين لهما معامل ارتباط r = 0.03. هذه القيمة قريبة من الصفر، مما يشير إلى عدم وجود علاقة عمليا بين المتغيرين.
بشكل عام، يعتبر حجم التأثير صغيرًا إذا كانت قيمة معامل ارتباط بيرسون r حوالي 0.1، ومتوسطًا إذا كانت r حوالي 0.3، وكبيرًا إذا كانت r تساوي أو أكبر من 0.5.
3. نسبة الأرجحية
عندما تريد دراسة احتمالات النجاح في مجموعة علاجية مقابل احتمالات النجاح في مجموعة مراقبة، فإن الطريقة الأكثر شيوعًا لحساب حجم التأثير هي استخدام نسبة الأرجحية .
على سبيل المثال، لنفترض أن لدينا الجدول التالي:
| حجم التأثير | #نجاح | #شطرنج |
|---|---|---|
| مجموعة العلاج | الى | ب |
| مجموعة التحكم | ضد | د |
سيتم حساب نسبة الأرجحية على النحو التالي:
نسبة الأرجحية = (م) / (قبل الميلاد)
كلما كانت نسبة الأرجحية أبعد من 1، كلما زاد احتمال أن يؤدي العلاج إلى تأثير حقيقي.
فوائد استخدام أحجام التأثير على القيم P
تتمتع أحجام التأثير بالعديد من المزايا مقارنة بالقيم p:
1. يساعدنا حجم التأثير في الحصول على فكرة أفضل عن مدى حجم الفرق بين مجموعتين أو مدى قوة الارتباط بين مجموعتين. يمكن للقيمة p أن تخبرنا فقط ما إذا كان هناك فرق كبير أو ارتباط كبير أم لا.
2. على عكس القيم الاحتمالية، يمكن استخدام أحجام التأثير لإجراء مقارنة كمية لنتائج الدراسات المختلفة التي تم إجراؤها في بيئات مختلفة. لهذا السبب، غالبًا ما تُستخدم أحجام التأثير في التحليلات التلوية.
3. يمكن أن تتأثر القيم P بأحجام العينات الكبيرة. كلما زاد حجم العينة، زادت القوة الإحصائية لاختبار الفرضيات، مما يسمح له باكتشاف حتى التأثيرات الصغيرة. وهذا يمكن أن يؤدي إلى انخفاض القيم الاحتمالية، على الرغم من أحجام التأثير الصغيرة التي قد لا يكون لها أي أهمية عملية.
مثال بسيط يمكن أن يوضح ذلك بوضوح: لنفترض أننا نريد أن نعرف ما إذا كانت طريقتان للدراسة تؤديان إلى درجات اختبار مختلفة. لدينا مجموعة مكونة من 20 طالبًا يستخدمون أسلوب دراسة واحدًا بينما تستخدم مجموعة أخرى مكونة من 20 طالبًا أسلوب دراسة مختلفًا. ثم نعطي كل طالب نفس الاختبار.
متوسط درجات المجموعة الأولى هو 90.65 ومتوسط درجات المجموعة الثانية هو 90.75 . الانحراف المعياري للعينة 1 هو 2.77 والانحراف المعياري للعينة 2 هو 2.78 .
عندما نقوم بإجراء اختبار t مستقل لعينتين، يتبين أن إحصائية الاختبار هي -0.113 والقيمة p المقابلة هي 0.91 . الفرق بين متوسط درجات الاختبار ليس له دلالة إحصائية.
ومع ذلك، ضع في اعتبارك ما إذا كانت أحجام العينات في العينتين 200 ، ولكن الوسائل والانحرافات المعيارية ظلت كما هي تمامًا.
في هذه الحالة، سيكشف اختبار t مستقل مكون من عينتين أن إحصائية الاختبار هي -1.97 والقيمة p المقابلة أقل بقليل من 0.05 . الفرق بين متوسط درجات الاختبار له دلالة إحصائية.
السبب الأساسي الذي يجعل أحجام العينات الكبيرة يمكن أن تؤدي إلى استنتاجات ذات دلالة إحصائية يرجع إلى الصيغة المستخدمة لحساب إحصائيات اختبار t :
إحصائية الاختبار t = [ ( x 1 – x 2 ) – d ] / (√ ق 2 1 / ن 1 + ق 2 2 / ن 2 )
لاحظ أنه عندما يكون n 1 و n 2 صغيرين، يكون المقام الصحيح لإحصائيات اختبار t صغيرًا. وعندما تقسم على عدد صغير، تحصل على عدد كبير. وهذا يعني أن إحصائيات اختبار t ستكون كبيرة وأن قيمة p المقابلة ستكون صغيرة، مما يؤدي إلى نتائج ذات دلالة إحصائية.
ما الذي يعتبر حجم تأثير جيد؟
السؤال الذي يطرحه الطلاب غالبًا هو: ما هو حجم التأثير الجيد؟
الإجابة المختصرة: لا يمكن أن يكون حجم التأثير “جيدًا” أو “سيئًا” لأنه يقيس ببساطة حجم الفرق بين مجموعتين أو قوة الارتباط بين مجموعتين.
ومع ذلك، يمكننا استخدام القواعد الأساسية التالية لتحديد ما إذا كان حجم التأثير صغيرًا أم متوسطًا أم كبيرًا:
كوهين د:
- يعتبر d الذي يبلغ 0.2 أو أقل حجم تأثير صغير.
- يعتبر d بمقدار 0.5 حجم تأثير متوسط.
- يعتبر d الذي يبلغ 0.8 أو أكبر حجم تأثير كبيرًا.
معامل ارتباط بيرسون
- تعتبر القيمة المطلقة لـ r حوالي 0.1 حجم تأثير صغير.
- تعتبر القيمة المطلقة لـ r حوالي 0.3 حجم تأثير متوسط.
- تعتبر القيمة المطلقة لـ r أكبر من 0.5 حجم تأثير كبير.
ومع ذلك، فإن تعريف الارتباط “القوي” يمكن أن يختلف من مجال إلى آخر. ارجع إلى هذه المقالة لفهم ما يعتبر ارتباطًا قويًا عبر الصناعات المختلفة بشكل أفضل.