كيفية حساب القيم p في excel (3 أمثلة)

في الإحصاء، نستخدماختبار الفرضيات لتحديد ما إذا كانت العبارة المتعلقة بالمعلمة السكانية صحيحة أم لا.

عندما نقوم بإجراء اختبار الفرضيات، غالبًا ما نحصل على إحصائية اختبار T-score.

بمجرد العثور على إحصائية اختبار t-score، يمكننا بعد ذلك العثور على القيمة p المرتبطة بها.

إذا كانت هذه القيمة الاحتمالية أقل من قيمة معينة (على سبيل المثال 0.10، 0.05، 0.01)، فإننا نرفض الفرضية الصفرية للاختبار ونستنتج أن نتائجنا ذات دلالة إحصائية.

توضح الأمثلة التالية كيفية حساب القيمة الاحتمالية لإحصائيات الاختبار في Excel في ثلاثة سيناريوهات مختلفة.

مثال 1: حساب قيمة P للاختبار ثنائي الطرف

لنفترض أن عالم النبات يريد معرفة ما إذا كان متوسط ارتفاع نوع معين من النباتات يساوي 15 بوصة.

وفي عينة عشوائية مكونة من 12 نباتًا، وجدت أن متوسط ارتفاع العينة هو 14.33 بوصة، والانحراف المعياري للعينة هو 1.37 بوصة.

يقوم بإجراء اختبار الفرضيات باستخدام الفرضيات الصفرية والبديلة التالية:

H ₀ (فرضية العدم): μ= 15 بوصة

_HA (فرضية بديلة): μ ≠ 15 بوصة

يتم حساب إحصائية الاختبار على النحو التالي:

• ر = ( X – μ) / (ق/ √n )
• ر = (14.33-15) / (1.37/√ 12 )
• ر = -1.694

درجات الحرية المرتبطة بإحصائيات الاختبار هذه هي n-1 = 12-1 = 11 .

للعثور على القيمة الاحتمالية لإحصائية الاختبار هذه، سنستخدم الصيغة التالية في Excel:

 =T.DIST.2T(ABS(-1.694), 11)

توضح لقطة الشاشة التالية كيفية استخدام هذه الصيغة عمليًا.

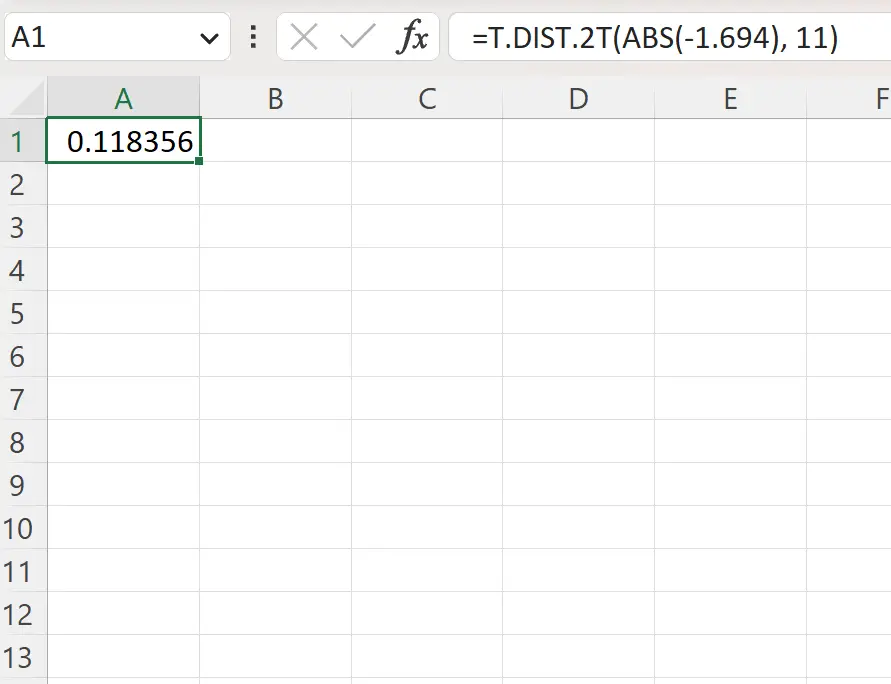
القيمة p ثنائية الذيل هي 0.1184 .

منذ هذه القيمة لا تقل عن 0.05، فشلنا في رفض الفرضية الصفرية. ليس لدينا ما يكفي من الأدلة لنقول أن متوسط ارتفاع النبات يختلف عن 15 بوصة.

مثال 2: احسب قيمة P للاختبار على اليسار

لنفترض أننا نفترض أن متوسط وزن أداة معينة يتم إنتاجها في المصنع هو 20 جرامًا. ومع ذلك، يقدر أحد المفتشين أن متوسط الوزن الفعلي أقل من 20 جرامًا.

ولاختبار ذلك، يقوم بوزن عينة عشوائية بسيطة مكونة من 20 عنصر واجهة مستخدم ويحصل على المعلومات التالية:

• ن = 20 الحاجيات
• س = 19.8 جرام
• ق = 3.1 جرام

ثم يقوم بإجراء اختبار الفرضيات باستخدام الفرضيات الصفرية والبديلة التالية:

H ₀ (فرضية فارغة): μ ≥ 20 جرام

_HA (فرضية بديلة): μ <20 جرام

يتم حساب إحصائية الاختبار على النحو التالي:

• ر = ( X – μ) / (ق/ √n )
• ر = (19.8-20) / (3.1/√ 20 )
• ر = -.2885

درجات الحرية المرتبطة بإحصائيات الاختبار هذه هي n-1 = 20-1 = 19 .

للعثور على القيمة الاحتمالية لإحصائية الاختبار هذه، سنستخدم الصيغة التالية في Excel:

 =T.DIST(-.2885, 19, TRUE)

توضح لقطة الشاشة التالية كيفية استخدام هذه الصيغة عمليًا.

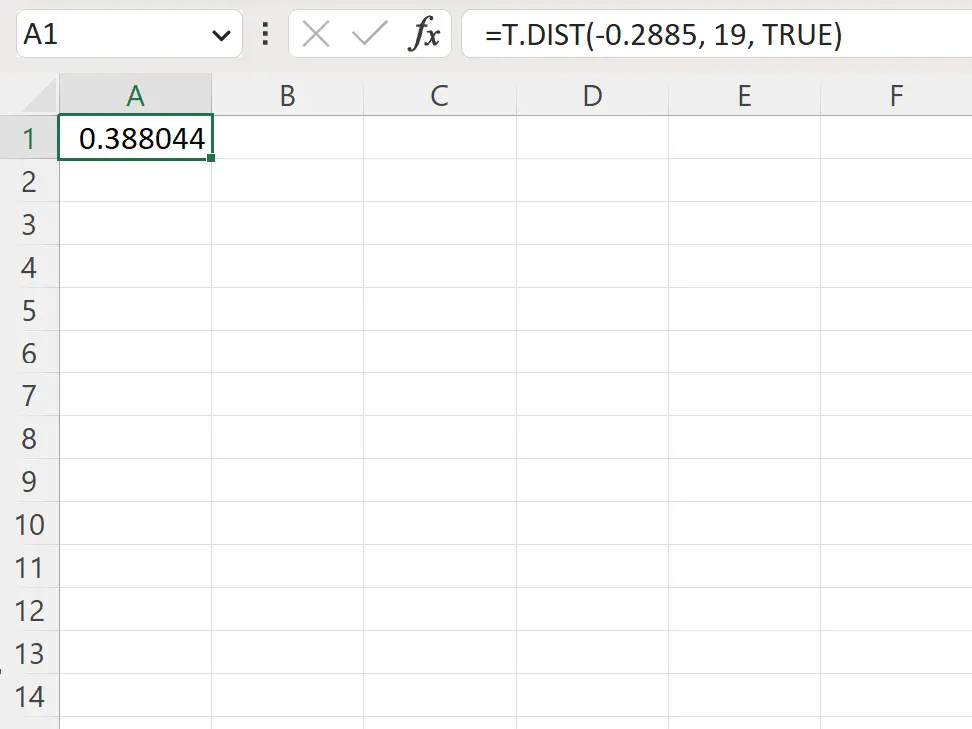
القيمة p على اليسار هي 0.388044 .

منذ هذه القيمة لا تقل عن 0.05 فإن المفتش يفشل في رفض الفرضية الصفرية. لا توجد أدلة كافية تشير إلى أن متوسط الوزن الفعلي للقطع المصغّرة المنتجة في هذا المصنع أقل من 20 جرامًا.

ملاحظة : استخدمنا الوسيطة TRUE لتحديد ضرورة استخدام دالة التوزيع التراكمي عند حساب القيمة الاحتمالية.

مثال 3: احسب قيمة P للاختبار ذي الطرف الأيمن

لنفترض أن متوسط ارتفاع نوع معين من النباتات هو 10 بوصات. ومع ذلك، يقول أحد علماء النبات أن متوسط الارتفاع الحقيقي هو أكثر من 10 بوصات.

ولاختبار هذا الادعاء، قامت بقياس ارتفاع عينة عشوائية بسيطة مكونة من 15 نباتًا وحصلت على المعلومات التالية:

• ن = 15 نباتًا
• س = 11.4 بوصة
• ق = 2.5 بوصة

ثم يقوم بإجراء اختبار الفرضيات باستخدام الفرضيات الصفرية والبديلة التالية:

H ₀ (فرضية العدم): μ ≥ 10 بوصة

_HA (فرضية بديلة): μ > 10 بوصات

يتم حساب إحصائية الاختبار على النحو التالي:

• ر = ( X – μ) / (ق/ √n )
• ر = (11.4-10) / (2.5/√ 15 )
• ر = 2.1689

درجات الحرية المرتبطة بإحصائيات الاختبار هذه هي n-1 = 15-1 = 14 .

للعثور على القيمة الاحتمالية لإحصائية الاختبار هذه، سنستخدم الصيغة التالية في Excel:

 =T.DIST.RT(2.1689, 14)

توضح لقطة الشاشة التالية كيفية استخدام هذه الصيغة عمليًا.

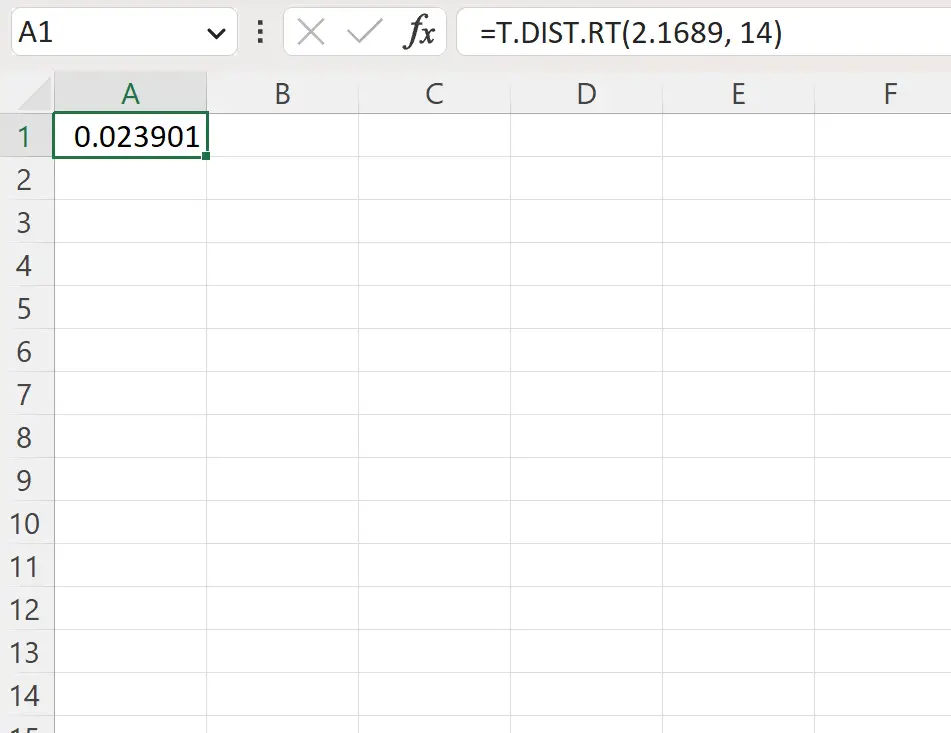
القيمة p على اليمين هي 0.023901 .

وبما أن هذه القيمة أقل من 0.05، فيمكن لعالم النبات رفض فرضية العدم. لديها ما يكفي من الأدلة لتقول أن متوسط الارتفاع الحقيقي لهذا النوع من النباتات يزيد عن 10 بوصات.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في Excel:

كيفية العثور على قيمة P من Z Score في Excel
كيفية العثور على القيمة P لإحصائيات F في Excel
كيفية العثور على القيمة P لإحصائيات مربع كاي في إكسيل