كيفية حساب الخطأ المعياري للمتوسط في excel

الخطأ المعياري للمتوسط هو وسيلة لقياس توزيع القيم في مجموعة البيانات. يتم حسابه على النحو التالي:

الخطأ المعياري = s / √n

ذهب:

• s : عينة الانحراف المعياري
• ن : حجم العينة

يمكنك حساب الخطأ القياسي لمتوسط أي مجموعة بيانات في Excel باستخدام الصيغة التالية:

= STDEV (نطاق القيم) / SQRT ( COUNT (نطاق القيم))

يوضح المثال التالي كيفية استخدام هذه الصيغة.

مثال: خطأ قياسي في Excel

لنفترض أن لدينا مجموعة البيانات التالية:

توضح لقطة الشاشة التالية كيفية حساب الخطأ المعياري للمتوسط لمجموعة البيانات هذه:

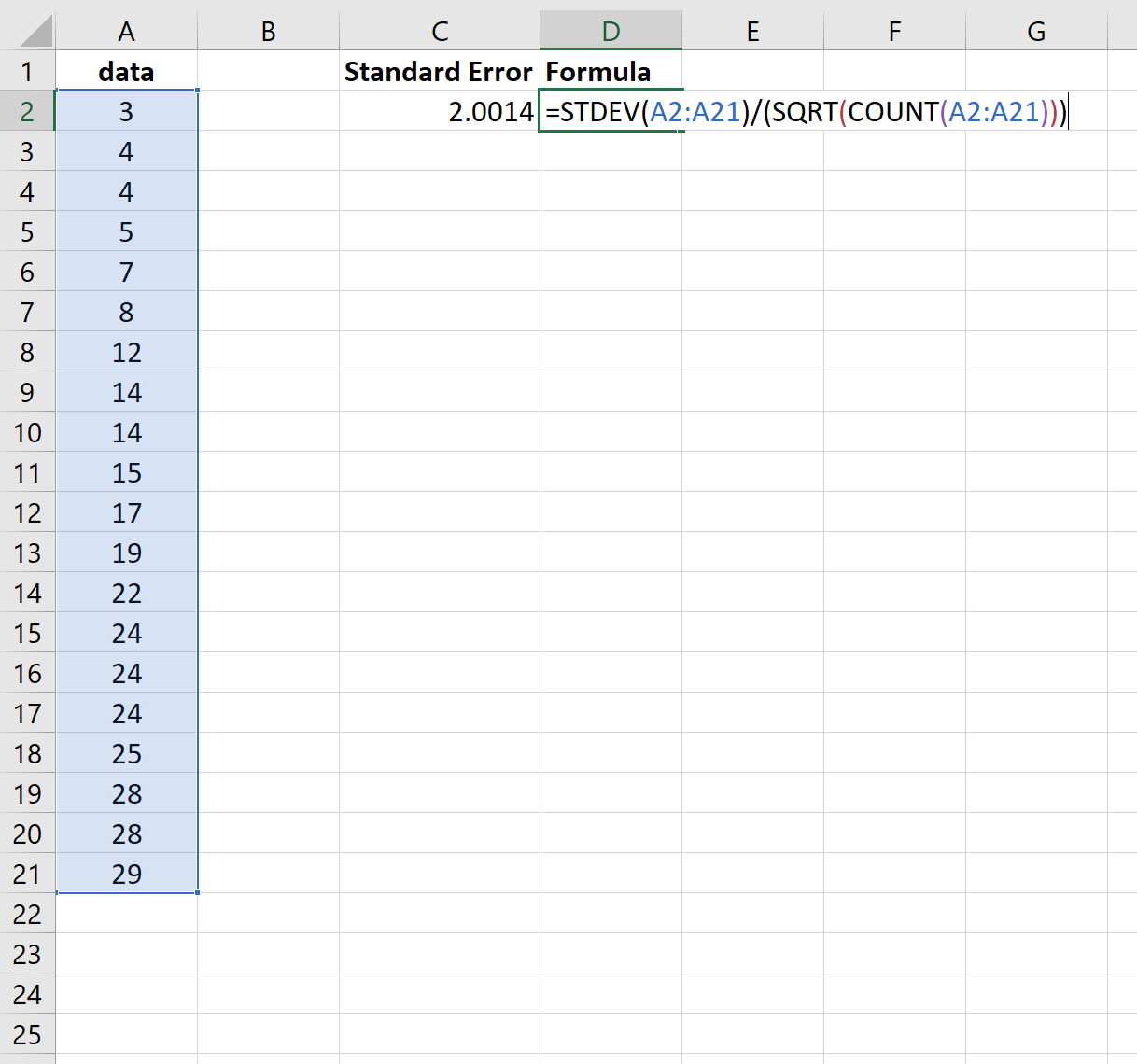
الخطأ القياسي تبين أنه 2.0014 .

لاحظ أن الدالة =STDEV() تحسب متوسط العينة، وهو ما يعادل الدالة =STDEV.S() في Excel.

لذا، كان بإمكاننا استخدام الصيغة التالية للحصول على نفس النتائج:

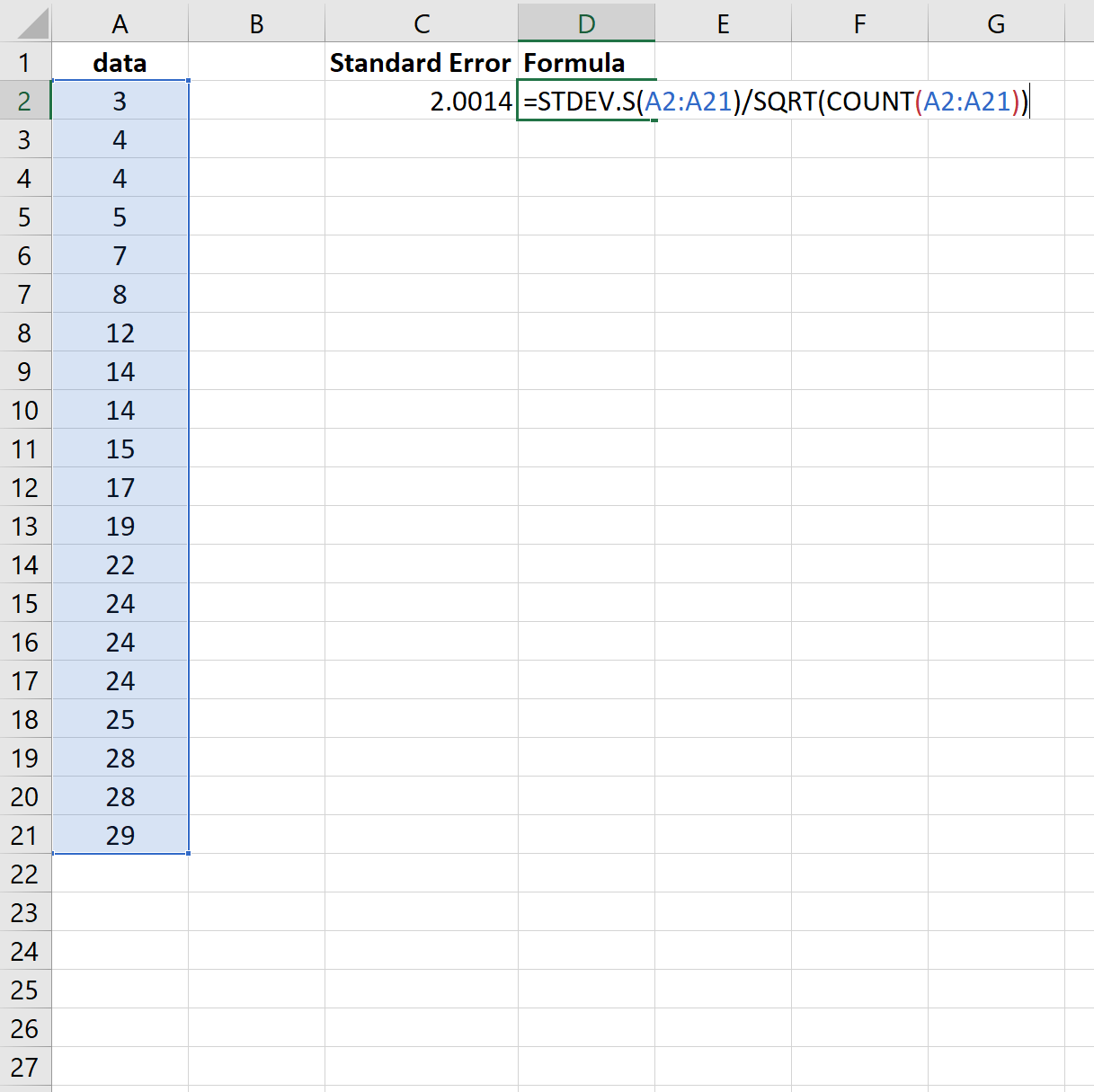
مرة أخرى، الخطأ القياسي هو 2.0014 .

كيفية تفسير الخطأ المعياري للمتوسط

الخطأ المعياري للوسط هو ببساطة مقياس لانتشار القيم حول المتوسط. هناك أمران يجب مراعاتهما عند تفسير الخطأ المعياري للمتوسط:

1. كلما زاد الخطأ المعياري للمتوسط، زادت تشتت القيم حول المتوسط في مجموعة البيانات.

لتوضيح ذلك، فكر فيما إذا قمنا بتغيير القيمة الأخيرة لمجموعة البيانات السابقة برقم أكبر بكثير:

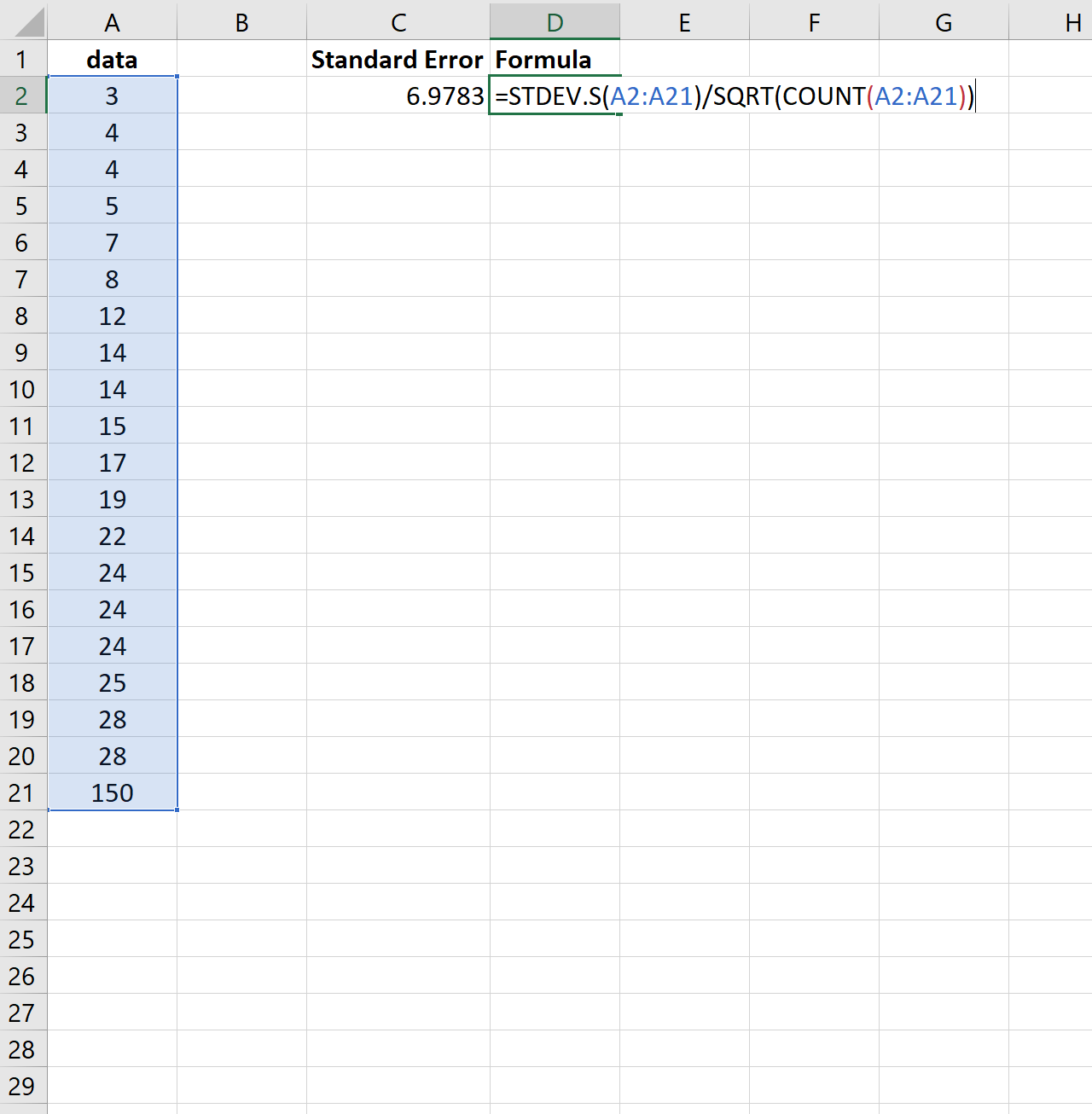
لاحظ كيف يزداد الخطأ القياسي من 2.0014 إلى 6.9783 . يشير هذا إلى أن القيم الموجودة في مجموعة البيانات هذه موزعة بشكل أكبر حول المتوسط مقارنة بمجموعة البيانات السابقة.

2. مع زيادة حجم العينة، يميل الخطأ المعياري للمتوسط إلى الانخفاض.

لتوضيح ذلك، ضع في اعتبارك الخطأ المعياري للمتوسط لمجموعتي البيانات التاليتين:

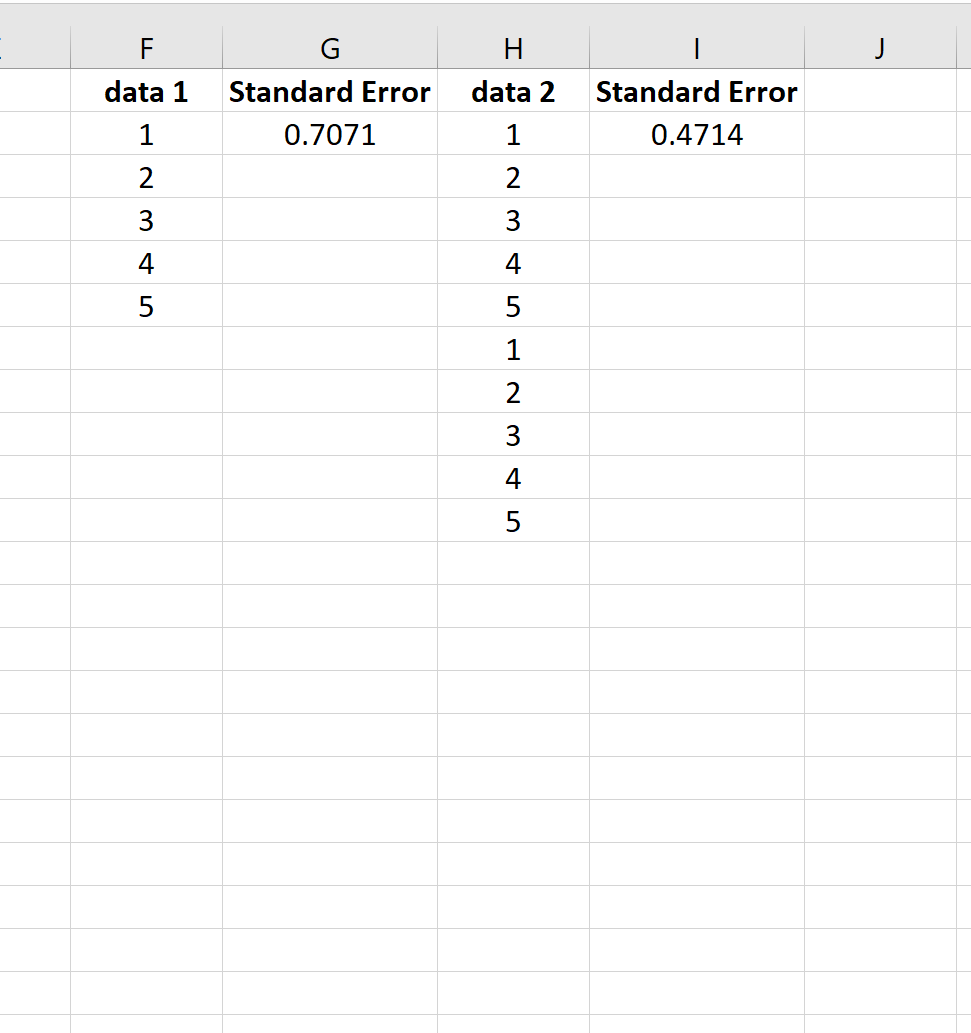
مجموعة البيانات الثانية هي ببساطة مجموعة البيانات الأولى التي تتكرر مرتين. لذا فإن كلا مجموعتي البيانات لهما نفس المتوسط، لكن مجموعة البيانات الثانية لها حجم عينة أكبر، وبالتالي بها خطأ معياري أصغر.