كيفية تنفيذ الانحدار التدريجي في sas (مع مثال)

الانحدار التدريجي هو إجراء يمكننا استخدامه لبناء نموذج انحدار من مجموعة من المتغيرات المتوقعة عن طريق إدخال وإزالة المتنبئات بطريقة خطوة بخطوة في النموذج حتى لا يوجد سبب صالح إحصائيًا للدخول أو حذف المزيد.

الهدف من الانحدار التدريجي هو إنشاء نموذج انحدار يتضمن جميع المتغيرات المتوقعة التي ترتبط بشكل كبير إحصائيًا بمتغير الاستجابة .

لإجراء الانحدار التدريجي في SAS، يمكنك استخدام PROC REG مع عبارة التحديد .

يوضح المثال التالي كيفية تنفيذ الانحدار التدريجي في SAS عمليًا.

مثال: تنفيذ الانحدار خطوة بخطوة في SAS

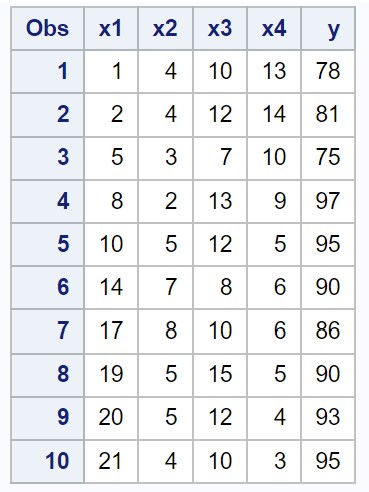
لنفترض أن لدينا مجموعة البيانات التالية في SAS التي تحتوي على أربعة متغيرات تنبؤية (x1، x2، x3، x4) ومتغير استجابة واحد (y):

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

لنفترض الآن أننا نريد تحديد مجموعة المتغيرات المتوقعة التي ستنتج أفضل نموذج انحدار خطي متعدد .

عندما نتحدث عن نموذج الانحدار “الأفضل”، فإننا نعني النموذج الذي يزيد أو يقلل من بعض التدابير.

هناك مقياسان نستخدمهما عادةً لتقييم نموذج الانحدار الأفضل بين مجموعة من النماذج المحتملة:

1. R-squared المعدلة : تخبرنا قيمة R-squared المعدلة بفائدة النموذج، ويتم تعديلها بناءً على عدد المتنبئين في النموذج. يعتبر النموذج ذو أعلى قيمة R-squared المعدلة هو الأفضل.

2. AIC : معيار معلومات Akaike (AIC) هو مقياس يستخدم لمقارنة ملاءمة نماذج الانحدار المختلفة. يعتبر النموذج ذو أدنى قيمة AIC هو الأفضل.

لحسن الحظ، يمكننا حساب قيم R-squared و AIC المجهزة لنماذج الانحدار في SAS باستخدام PROC REG مع عبارة SELECTION .

يوضح الكود التالي كيفية القيام بذلك:

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

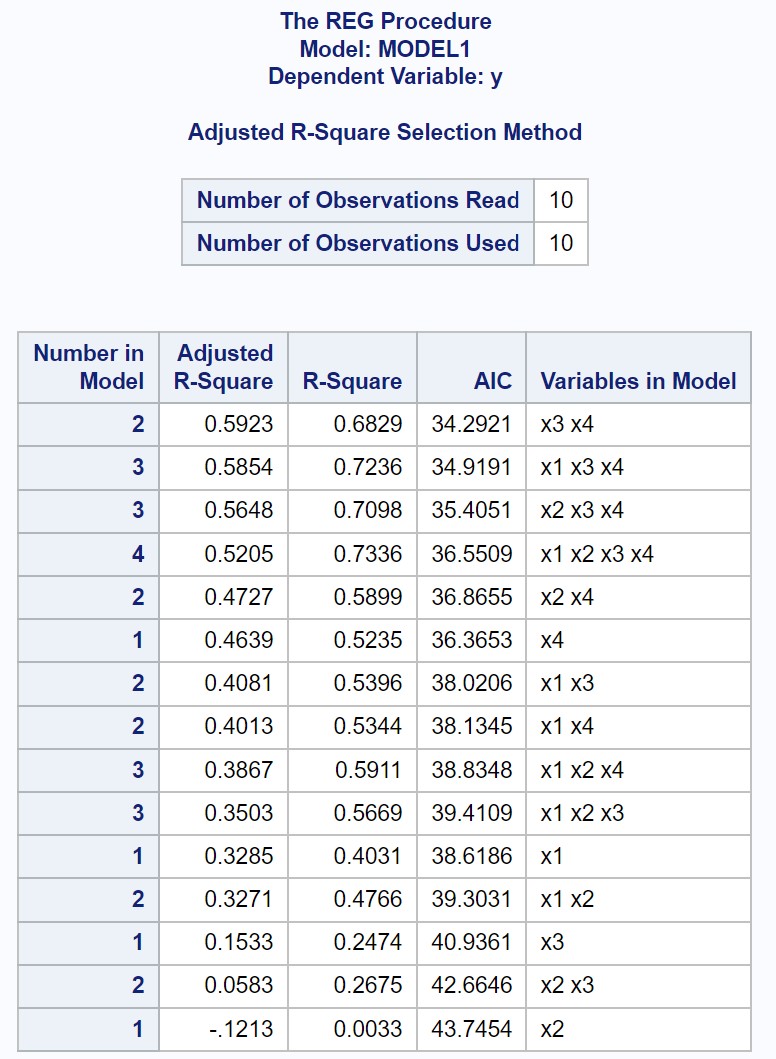
يعرض الإخراج قيم R-squared و AIC المجهزة لكل نموذج انحدار خطي متعدد محتمل.

من النتيجة، يمكننا أن نرى أن القيمة ذات أعلى قيمة مربعة R معدلة وأقل قيمة AIC هي نموذج الانحدار الذي يستخدم فقط x3 وx4 كمتغيرات تنبؤية.

وبهذا نعلن أن النموذج التالي هو “الأفضل” من بين جميع النماذج الممكنة:

ص = ب ₀ + ب ₁ (x3) + ب ₂ (x4)

يحتوي نموذج الانحدار الخاص هذا على المقاييس التالية:

• قيمة R-squared المعدلة: 0.5923
• إيك: 34.2921

ملاحظات حول اختيار نموذج الانحدار “الأفضل”.

لاحظ أنه في بعض الأحيان، لا يحتوي النموذج ذو أعلى قيمة R-squared المعدلة دائمًا على أدنى قيمة AIC.

عندما يتعلق الأمر بتحديد نموذج الانحدار الأفضل، فإن R-squared وAIC المعدلين يعملان كاقتراحات، ولكن في العالم الحقيقي قد تحتاج إلى استخدام خبرة المجال لتحديد النموذج الأفضل.

قد يكون من الحكمة أيضًا اختيار نموذج شحيح ، أي نموذج يحقق المستوى المطلوب من الملاءمة باستخدام أقل عدد ممكن من المتغيرات المتوقعة.

ينبع السبب وراء هذا النوع من النماذج من فكرة شفرة أوكام (التي تسمى أحيانًا “مبدأ البخل”) والتي تقول إن التفسير الأبسط هو على الأرجح التفسير الصحيح.

عند تطبيقها على الإحصائيات، يجب تفضيل النموذج الذي يحتوي على عدد قليل من المعلمات ولكنه يحقق مستوى مُرضيًا من الملاءمة على النموذج الذي يحتوي على عدد كبير من المعلمات ولا يحقق سوى مستوى أعلى قليلاً من الملاءمة.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في SAS:

كيفية إجراء الانحدار الخطي البسيط في SAS
كيفية إجراء الانحدار الخطي المتعدد في SAS
كيفية إجراء الانحدار متعدد الحدود في SAS
كيفية إجراء الانحدار اللوجستي في SAS