ما هي الدقة المتوازنة؟ (التعريف & #038؛ مثال)

الدقة المتوازنة هي مقياس يمكننا استخدامه لتقييم أداء نموذج التصنيف .

يتم حسابه على النحو التالي:

الدقة المتوازنة = (الحساسية + النوعية) / 2

ذهب:

• الحساسية : “المعدل الإيجابي الحقيقي” – النسبة المئوية للحالات الإيجابية التي يستطيع النموذج اكتشافها.
• الخصوصية : “المعدل السلبي الحقيقي” – النسبة المئوية للحالات السلبية التي يستطيع النموذج اكتشافها.

يكون هذا المقياس مفيدًا بشكل خاص عندما تكون الفئتان غير متوازنتين، أي أن إحدى الفئتين تظهر أكثر بكثير من الأخرى.

يوضح المثال التالي كيفية حساب الدقة المتوازنة عمليًا ويوضح سبب كونها مقياسًا مفيدًا.

مثال: حساب الدقة المتوازنة

لنفترض أن أحد المحللين الرياضيين يستخدم نموذج الانحدار اللوجستي للتنبؤ بما إذا كان سيتم ضم 400 لاعب كرة سلة جامعي مختلف إلى الدوري الاميركي للمحترفين أم لا.

تلخص مصفوفة الارتباك التالية التنبؤات التي قدمها النموذج:

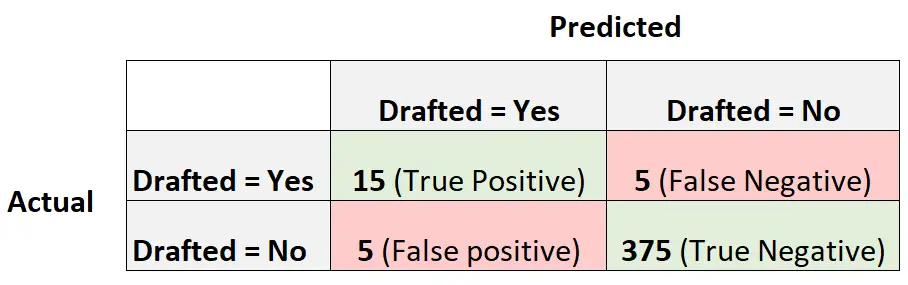
لحساب الدقة المتوازنة للنموذج، سنقوم أولاً بحساب الحساسية والنوعية:

• الحساسية : “المعدل الإيجابي الحقيقي” = 15 / (15 + 5) = 0.75
• الخصوصية : “المعدل السلبي الحقيقي” = 375 / (375 + 5) = 0.9868

يمكننا بعد ذلك حساب الدقة المتوازنة على النحو التالي:

• الدقة المتوازنة = (الحساسية + النوعية) / 2
• الدقة المتوازنة = (0.75 + 9868) / 2
• الدقة المتوازنة = 0.8684

وتبين أن الدقة المتوازنة للنموذج هي 0.8684 .

لاحظ أنه كلما اقتربت الدقة المتوازنة من 1، زادت قدرة النموذج على تصنيف الملاحظات بشكل صحيح.

في هذا المثال، تكون الدقة المتوازنة عالية جدًا، مما يخبرنا أن نموذج الانحدار اللوجستي يقوم بعمل جيد جدًا في التنبؤ بما إذا كان سيتم تجنيد اللاعبين الجامعيين في الدوري الاميركي للمحترفين أم لا.

في هذا السيناريو، نظرًا لأن الفئات غير متوازنة للغاية (تمت صياغة 20 لاعبًا ولم تتم صياغة 380 لاعبًا)، فإن الدقة المتوازنة تمنحنا صورة أكثر واقعية لأداء النموذج مقارنة بمقياس الدقة الإجمالي.

على سبيل المثال، يمكننا حساب دقة النموذج على النحو التالي:

• الدقة = (TP + TN) / (TP + TN + FP + FN)
• الدقة = (15 + 375) / (15 + 375 + 5 + 5)
• الدقة = 0.975

دقة النموذج هي 0.975 ، والتي تبدو عالية للغاية.

ومع ذلك، فكر في نموذج يتنبأ ببساطة بأن كل لاعب لن يتم تصميمه. سيكون لها دقة 380/400 = 0.95 . وهذا أقل قليلاً من دقة نموذجنا.

تمنحنا درجة الدقة المتوازنة البالغة 0.8684 فكرة أفضل عن قدرة النموذج على التنبؤ بكلا الفئتين.

بمعنى آخر، إنه يعطينا فكرة أفضل عن قدرة النموذج على التنبؤ باللاعبين الذين سيذهبون دون صياغة وأيهم سيذهبون.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إنشاء مصفوفة ارتباك في برامج إحصائية مختلفة:

كيفية إنشاء مصفوفة الارتباك في إكسيل
كيفية إنشاء مصفوفة الارتباك في R
كيفية إنشاء مصفوفة الارتباك في بايثون