ذات الحدين السلبي مقابل بواسون: كيفية اختيار نموذج الانحدار

الانحدار السلبي ذو الحدين وانحدار بواسون هما نوعان من نماذج الانحدار التي يجب استخدامها عندما يتم تمثيل متغير الاستجابة بنتائج العد المنفصلة.

فيما يلي بعض الأمثلة على متغيرات الاستجابة التي تمثل نتائج العد المنفصلة:

• عدد الطلاب المتخرجين من برنامج معين
• عدد حوادث الطرق عند تقاطع معين
• عدد المشاركين الذين أكملوا الماراثون
• عدد المرتجعات في شهر معين في متجر بيع بالتجزئة

إذا كان التباين يساوي المتوسط تقريبًا، فإن نموذج انحدار بواسون يناسب بشكل عام مجموعة البيانات بشكل جيد.

ومع ذلك، إذا كان التباين أكبر بكثير من المتوسط، فإن نموذج الانحدار السلبي ذو الحدين يكون قادرًا بشكل عام على ملاءمة البيانات بشكل أفضل.

هناك طريقتان يمكننا استخدامهما لتحديد ما إذا كان انحدار بواسون أو الانحدار السلبي ذو الحدين أكثر ملاءمة لمجموعة بيانات معينة:

1. قطع الأراضي المتبقية

يمكننا إنشاء مخطط للبقايا الموحدة مقابل القيم المتوقعة من نموذج الانحدار.

إذا كانت غالبية القيم المتبقية القياسية تتراوح بين -2 و2، فمن المحتمل أن يكون نموذج انحدار بواسون مناسبًا.

ومع ذلك، إذا كانت العديد من القيم المتبقية تقع خارج هذا النطاق، فمن المرجح أن يوفر نموذج الانحدار السلبي ذو الحدين ملاءمة أفضل.

2. اختبار نسبة الاحتمالية

يمكننا ملاءمة نموذج انحدار بواسون ونموذج الانحدار السلبي ذي الحدين مع نفس مجموعة البيانات ثم إجراء اختبار نسبة الاحتمالية.

إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية (على سبيل المثال 0.05)، فيمكننا أن نستنتج أن نموذج الانحدار السلبي ذو الحدين يوفر ملاءمة أفضل بكثير.

يوضح المثال التالي كيفية استخدام هاتين التقنيتين في R لتحديد ما إذا كان من الأفضل استخدام نموذج انحدار بواسون أو نموذج الانحدار السلبي ذي الحدين لمجموعة بيانات معينة.

مثال: الانحدار السلبي ذو الحدين مقابل انحدار بواسون

لنفترض أننا نريد معرفة عدد المنح الدراسية التي يتلقاها لاعب البيسبول في المدرسة الثانوية في مقاطعة معينة بناءً على قسم مدرسته (“أ” أو “ب” أو “ج”) ودرجته المدرسية. امتحان القبول بالجامعة (يقاس من 0 إلى 100). ).

استخدم الخطوات التالية لتحديد ما إذا كان نموذج الانحدار السلبي ذو الحدين أو نموذج انحدار بواسون يوفر ملاءمة أفضل للبيانات.

الخطوة 1: إنشاء البيانات

ينشئ التعليمة البرمجية التالية مجموعة البيانات التي سنعمل معها، والتي تتضمن بيانات عن 1000 لاعب بيسبول:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

الخطوة 2: ملاءمة نموذج انحدار بواسون ونموذج الانحدار السلبي ذي الحدين

يوضح التعليمة البرمجية التالية كيفية ملاءمة كل من نموذج انحدار بواسون ونموذج الانحدار السلبي ذي الحدين مع البيانات:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

الخطوة 3: إنشاء قطع الأراضي المتبقية

يوضح الكود التالي كيفية إنتاج قطع الأراضي المتبقية لكلا النموذجين.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

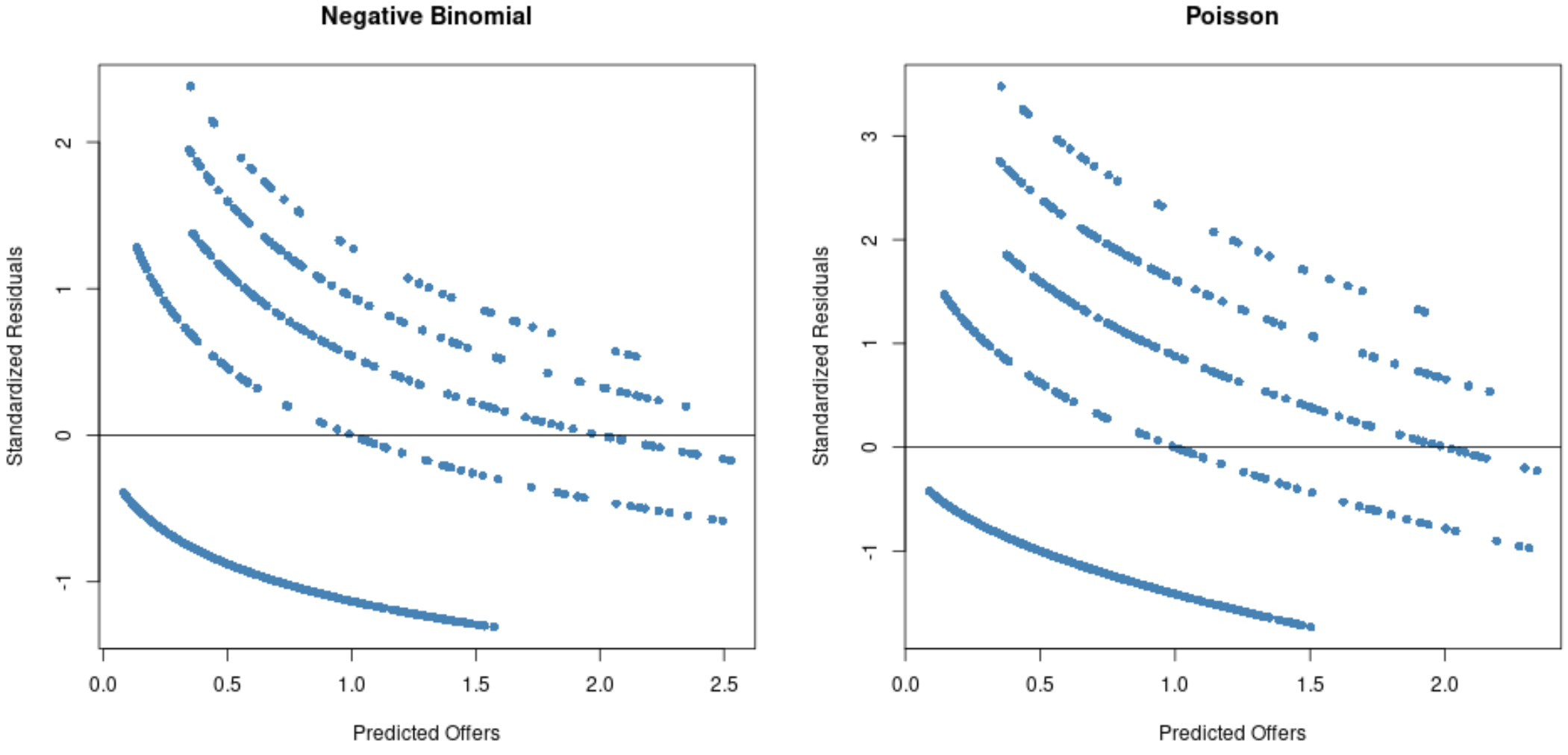
من خلال الرسوم البيانية، يمكننا أن نرى أن البقايا منتشرة بشكل أكبر لنموذج انحدار بواسون (لاحظ أن بعض البقايا تمتد إلى ما بعد 3) مقارنة بنموذج الانحدار السلبي ذي الحدين.

وهذه علامة على أن نموذج الانحدار السلبي ذي الحدين ربما يكون أكثر ملاءمة لأن بقايا هذا النموذج أصغر.

الخطوة 4: إجراء اختبار نسبة الاحتمالية

أخيرًا، يمكننا إجراء اختبار نسبة الاحتمالية لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية في ملاءمة نموذجي الانحدار:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

تبين أن القيمة p للاختبار هي 3.508072e-29 ، وهي أقل بكثير من 0.05.

وبالتالي، فإننا نستنتج أن نموذج الانحدار السلبي ذو الحدين يوفر ملاءمة أفضل بكثير للبيانات مقارنة بنموذج انحدار بواسون.

مصادر إضافية

مقدمة للتوزيع السلبي ذو الحدين
مقدمة لتوزيع بواسون