كيفية رسم التوزيع ذي الحدين في r

لرسم دالة الكتلة الاحتمالية للتوزيع ذي الحدين في R، يمكننا استخدام الوظائف التالية:

• dbinom(x, size, prob) لإنشاء دالة الكتلة الاحتمالية
• مؤامرة (x، y، type = ‘h’) لرسم دالة الكتلة الاحتمالية، مع تحديد أن المؤامرة عبارة عن رسم بياني (type = ‘h’)

لرسم دالة الكتلة الاحتمالية، ما عليك سوى تحديد الحجم   (على سبيل المثال، عدد التجارب) والاحتمال (على سبيل المثال، احتمال النجاح في تجربة معينة) في وظيفة dbinom() .

على سبيل المثال، يوضح التعليمة البرمجية التالية كيفية رسم دالة احتمالية جماعية لتوزيع ذي الحدين بالحجم = 20 وprob = 0.3:

 success <- 0:20

plot(success, dbinom(success, size=20, prob=.3), type='h')

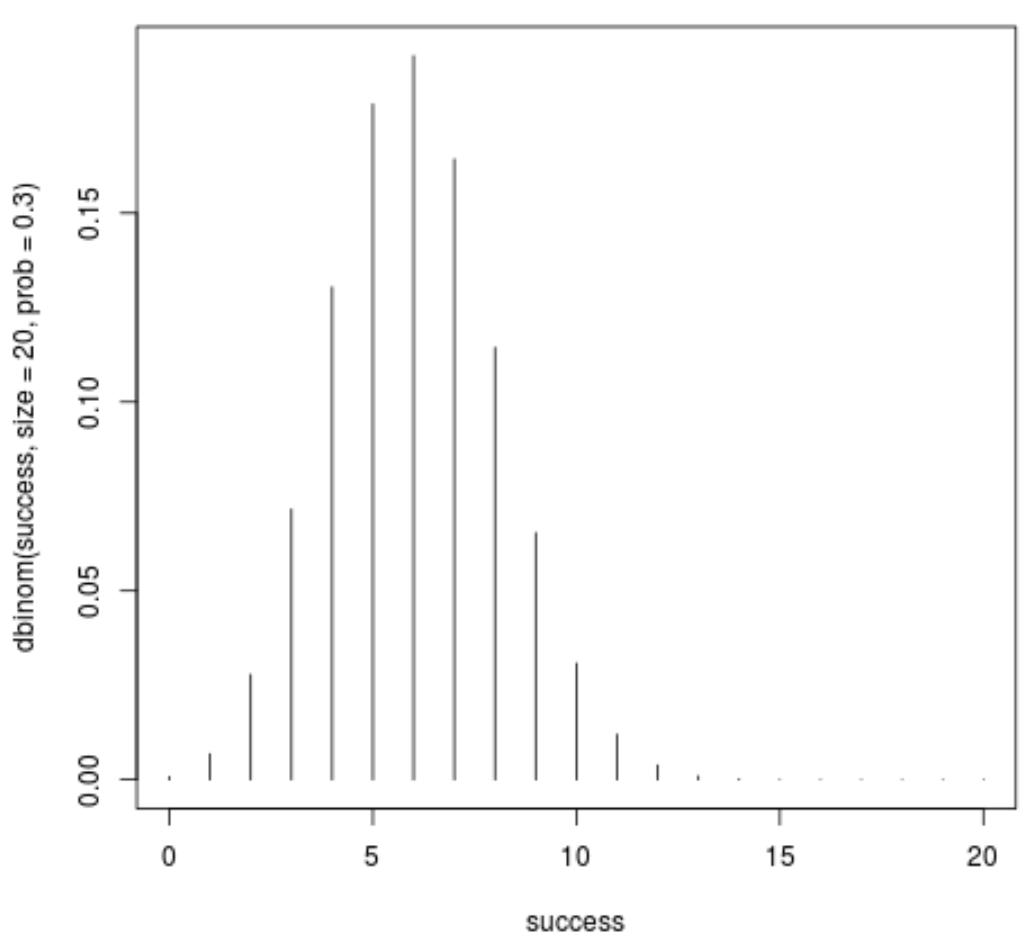
يوضح المحور السيني عدد النجاحات ويظهر المحور الصادي احتمالية الحصول على هذا العدد من النجاحات في 20 تجربة.

يمكننا إضافة عنوان وتغيير تسميات المحاور وزيادة عرض الخطوط لجعل الحبكة أكثر جمالية:

 success <- 0:20

plot(success,dbinom(success,size=20,prob=.3),
     type='h',
     main='Binomial Distribution (n=20, p=0.3)',
     ylab='Probability',
     xlab ='# Successes',
     lwd=3)

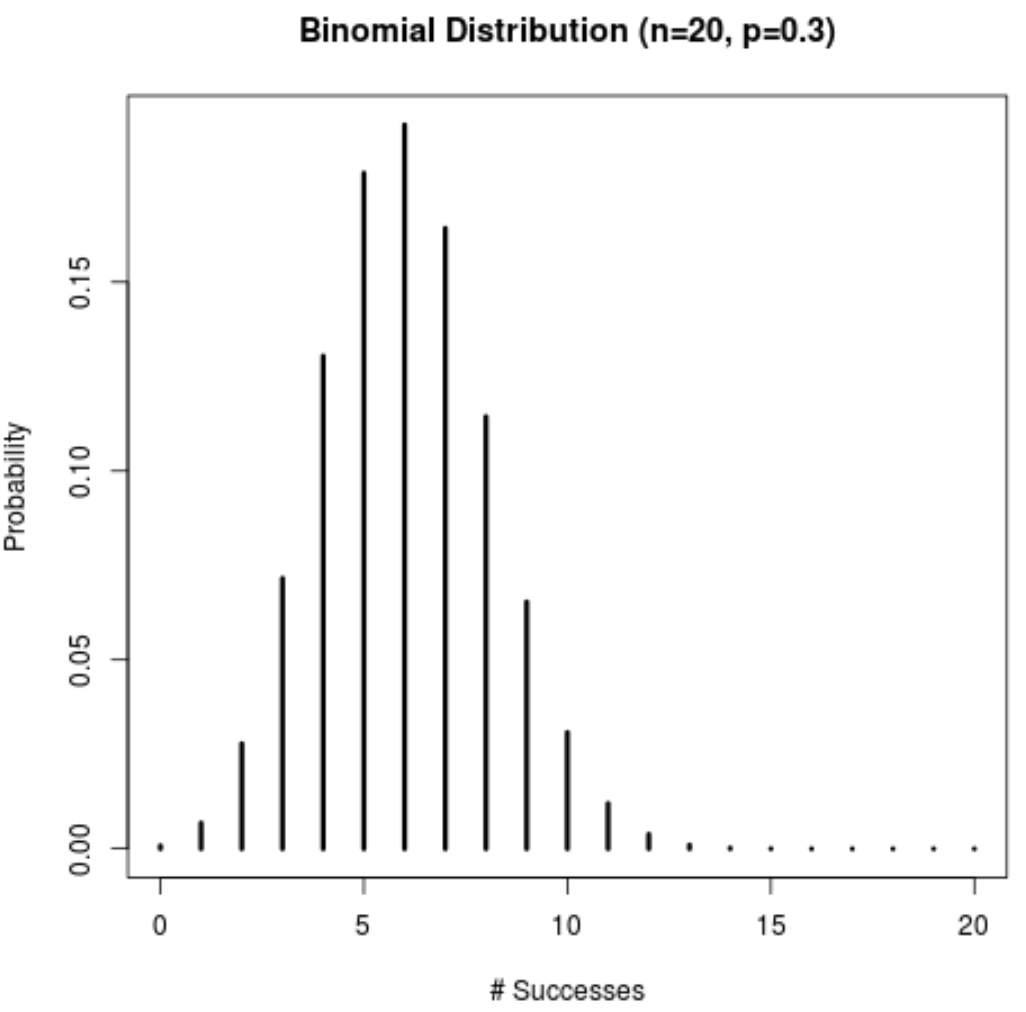
يمكنك استخدام الكود التالي للحصول على الاحتمالات الفعلية لكل عدد من النجاحات المعروضة في المخطط:

 #prevent R from displaying numbers in scientific notation
options(scipen=999) 

#define range of successes
success <- 0:20

#display probability of success for each number of trials
dbinom(success, size=20, prob=.3)

[1] 0.00079792266297612 0.00683933711122388 0.02784587252426865
[4] 0.07160367220526231 0.13042097437387065 0.17886305056987975
[7] 0.19163898275344257 0.16426198521723651 0.11439673970486122
[10] 0.06536956554563482 0.03081708090008504 0.01200665489613703
[13] 0.00385928193090119 0.00101783259716075 0.00021810698510587
[16] 0.00003738976887529 0.00000500755833151 0.00000050496386536
[19] 0.00000003606884753 0.00000000162716605 0.00000000003486784

مصادر إضافية

مقدمة للتوزيع ذي الحدين
فهم شكل التوزيع ذي الحدين