كيفية استخدام وظيفة logest في جداول بيانات google (مع مثال)

يمكنك استخدام الدالة LOGEST في جداول بيانات Google لحساب صيغة المنحنى الأسي الذي يناسب بياناتك.

وستكون معادلة المنحنى بالشكل التالي:

ص = ب* ^مكس

تستخدم هذه الوظيفة بناء الجملة الأساسي التالي:

 = LOGEST ( known_data_y, [known_data_x], [b], [verbose] )

ذهب:

• known_data_y : مصفوفة من قيم y المعروفة
• known_data_x : مصفوفة من قيم x المعروفة
• ب : وسيطة اختيارية. إذا كان TRUE، تتم معالجة الثابت b بشكل طبيعي. إذا كانت القيمة FALSE، يتم تعيين الثابت b على 1.
• مطول : حجة اختيارية. إذا كانت القيمة TRUE، فسيتم إرجاع إحصائيات الانحدار الإضافية. إذا كانت FALSE، فلن يتم إرجاع إحصائيات الانحدار الإضافية.

يوضح المثال التالي خطوة بخطوة كيفية استخدام هذه الوظيفة عمليًا.

الخطوة 1: أدخل البيانات

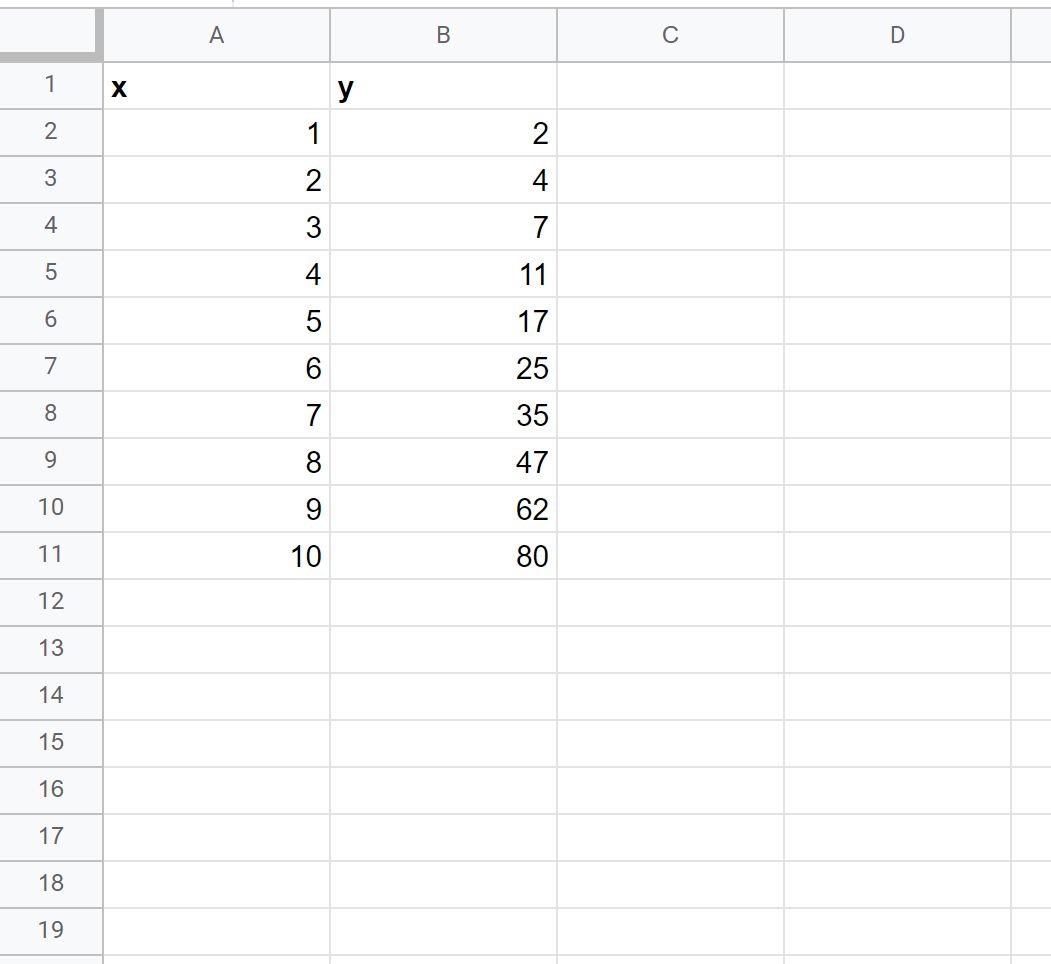
أولاً، دعنا ندخل مجموعة البيانات التالية في جداول بيانات Google:

الخطوة 2: تصور البيانات

بعد ذلك، لنقم بإنشاء مخطط تشتت سريع لـ x مقابل y للتحقق من أن البيانات تتبع بالفعل منحنى أسيًا:

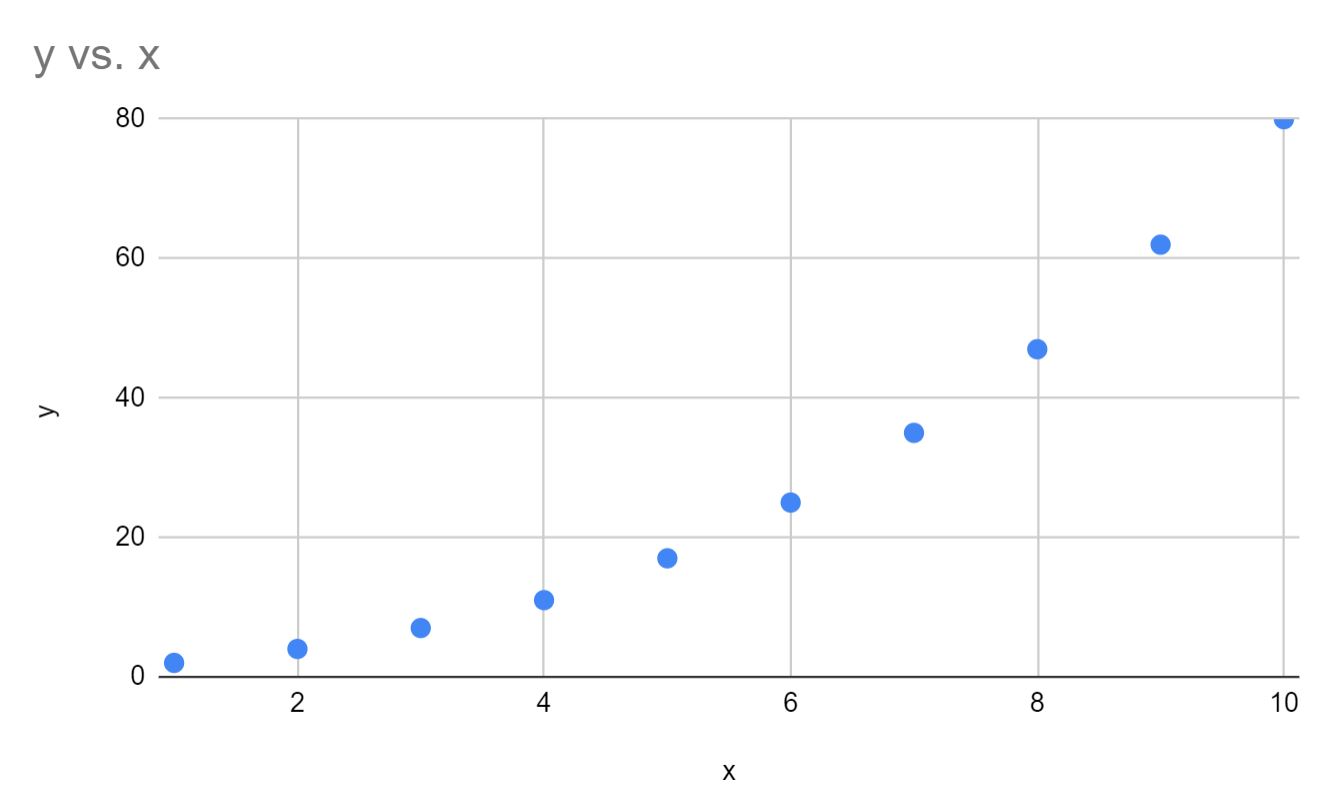
يمكننا أن نرى أن البيانات تتبع بالفعل منحنى أسيًا.

الخطوة 3: استخدم LOGEST للعثور على صيغة المنحنى الأسي

ثم يمكننا كتابة الصيغة التالية في أي خلية لحساب صيغة المنحنى الأسي:

 =LOGEST( B2:B11 , A2:A11 )

توضح لقطة الشاشة التالية كيفية استخدام هذه الصيغة عمليًا:

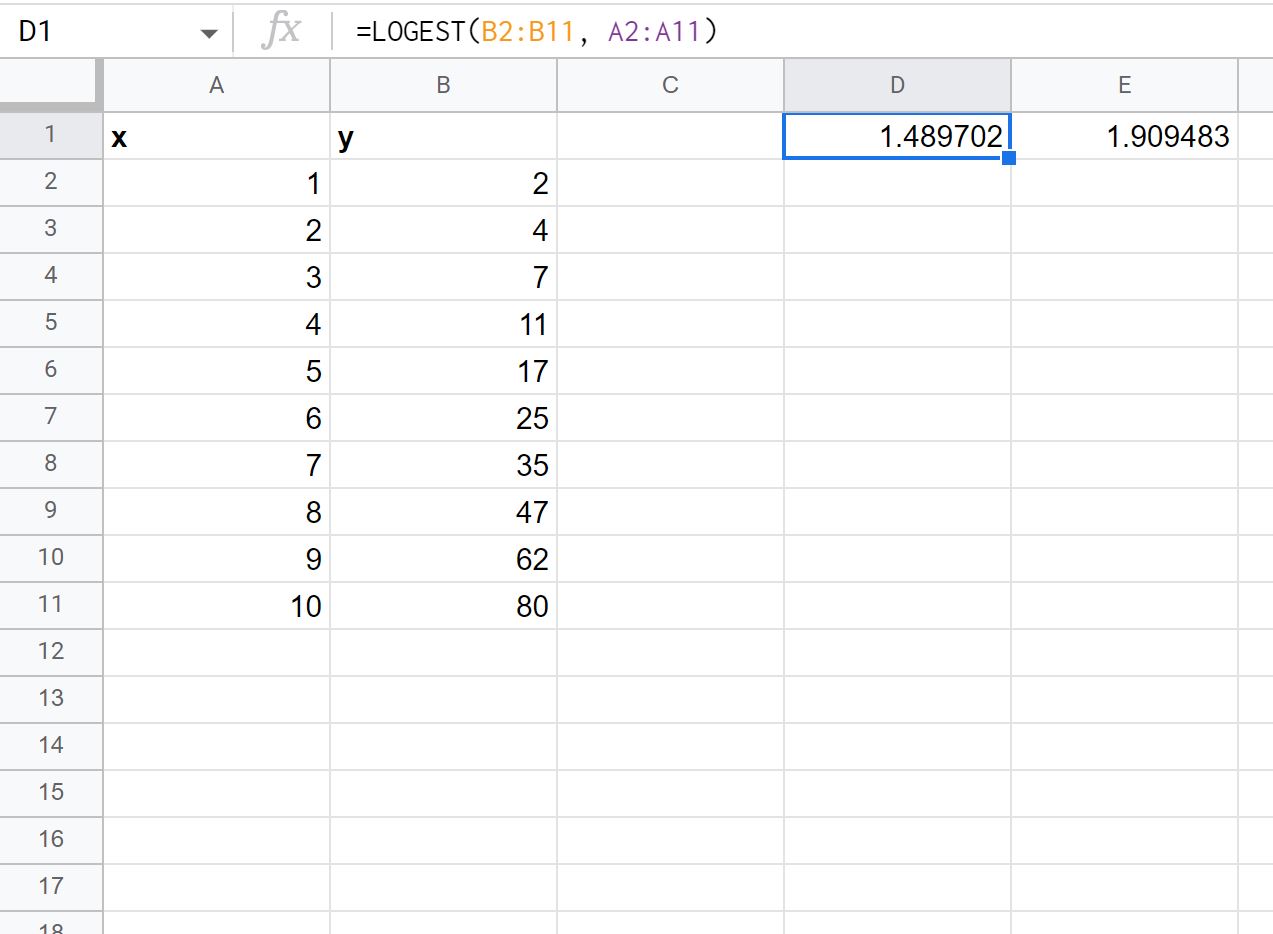
تمثل القيمة الأولى للمخرج قيمة m وتمثل القيمة الثانية للمخرج قيمة b في المعادلة:

ص = ب* ^مكس

لذلك، نكتب صيغة المنحنى الأسي على النحو التالي:

ص = 1.909483 * ^1.489702x

يمكننا بعد ذلك استخدام هذه الصيغة للتنبؤ بقيم y بناءً على قيمة x.

على سبيل المثال، إذا كانت قيمة xa 8، فإننا نتوقع أن تكون قيمة y 46.31 :

ص = 1.909483 * 1.489702 ⁸ = 46.31

الخطوة 4 (اختياري): عرض إحصائيات الانحدار الإضافية

يمكننا تعيين قيمة الوسيطة التفصيلية في الدالة LOGEST تساوي TRUE لعرض إحصائيات الانحدار الإضافية لمعادلة الانحدار المجهزة:

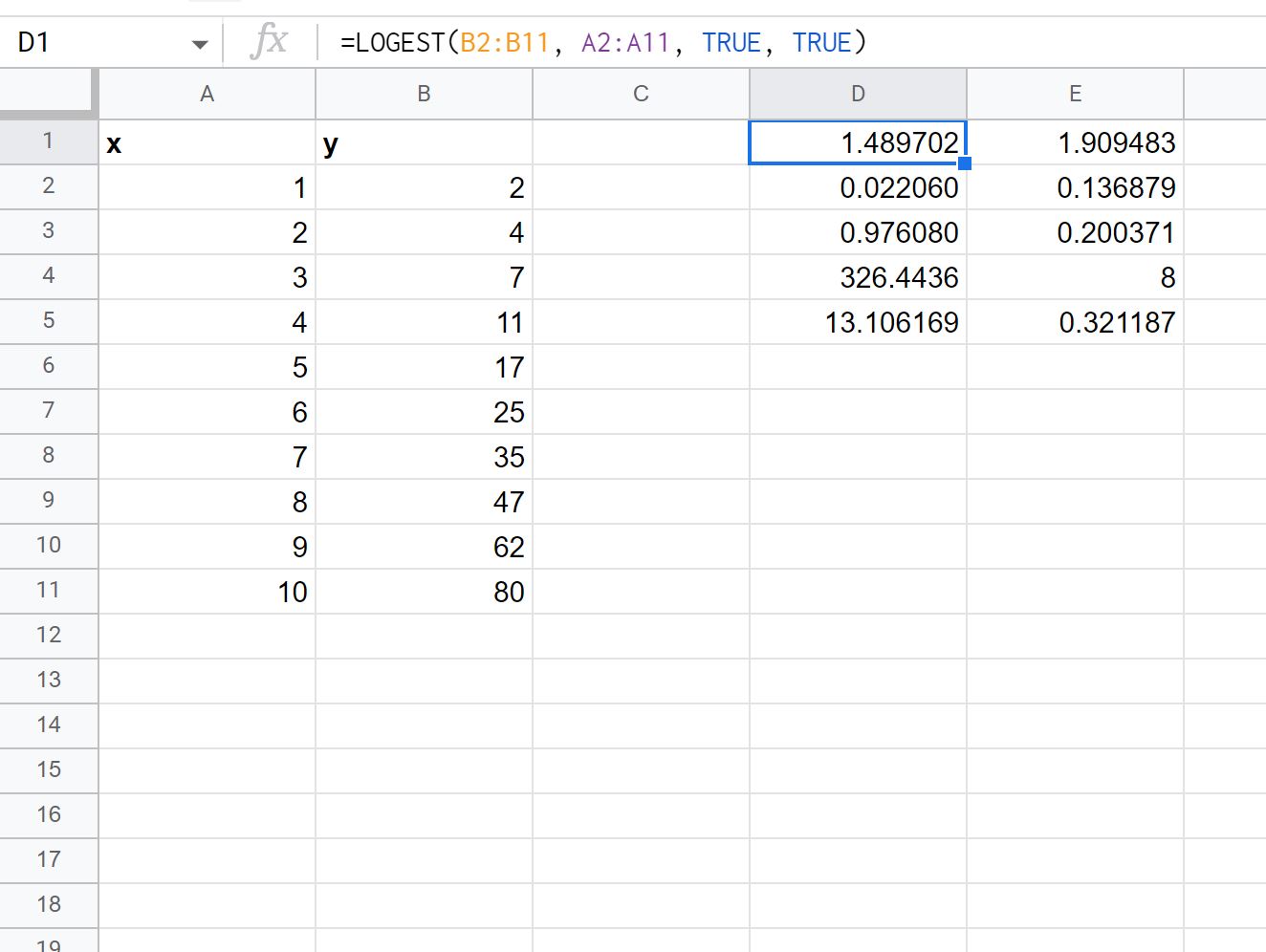
وإليك كيفية تفسير كل قيمة في النتيجة:

• الخطأ القياسي لـ m هو 0.02206 .
• الخطأ القياسي لـ b هو 0.136879 .
• R ² للنموذج هو .97608 .
• الخطأ القياسي لـ y هو .200371 .
• إحصائيات F هي 326.4436 .
• درجات الحرية هي 8 .
• مجموع انحدار المربعات هو 13.106169 .
• مجموع المربعات المتبقية هو 0.321187 .

وبشكل عام، فإن المقياس الأكثر أهمية في هذه الإحصائيات الإضافية هو قيمة ^R2 ، والتي تمثل نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بواسطة المتغير المتنبئ.

يمكن أن تختلف قيمة ^R2 من 0 إلى 1.

وبما أن R ² لهذا النموذج بالذات قريب من 1، فهذا يخبرنا أن المتغير المتنبئ x يتنبأ بقيمة متغير الاستجابة y جيدًا.

ذات صلة: ما هي قيمة R-squared الجيدة؟

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية القيام بأشياء شائعة أخرى في جداول بيانات Google:

كيفية إجراء الانحدار الخطي في جداول بيانات Google
كيفية إجراء الانحدار متعدد الحدود في جداول بيانات Google
كيفية حساب R-squared في جداول بيانات Google