كيفية تفسير سيج. القيم ( ذات الوجهين ) في برنامج spss
في كثير من الأحيان، عند إجراء اختبار إحصائي في SPSS، يحتوي جدول الإخراج على Sig. القيمة (الثنائية) .
تمثل هذه القيمة القيمة p على الوجهين للاختبار.
إذا كانت هذه القيمة أقل من مستوى الأهمية الخاص بك (الاختيارات الشائعة هي 0.05 أو 0.01)، فيمكنك رفض الفرضية الصفرية للاختبار الخاص بك.
يقدم هذا البرنامج التعليمي أمثلة حول كيفية تفسير Sig. (ثنائية) القيمة للاختبارات الإحصائية المختلفة.
مثال 1: اختبار t لعينة واحدة
يتم استخدام اختبار t لعينة واحدة لاختبار ما إذا كان متوسط المجتمع يساوي قيمة معينة أم لا.
على سبيل المثال، لنفترض أن عالم النبات يريد معرفة ما إذا كان متوسط ارتفاع نوع معين من النباتات يساوي 15 بوصة. أخذت عينة عشوائية من 12 نباتًا وسجلت ارتفاع كل منها بالبوصة.
ثم يستخدم هذه العينة لإجراء اختبار t لعينة واحدة مع الفرضيات الصفرية والبديلة التالية:
- H 0 : μ = 15 (متوسط عدد السكان الحقيقي يساوي 15 بوصة)
- H A : μ ≠ 15 (متوسط السكان الفعلي لا يساوي 15 بوصة)
قامت بإجراء اختبار t لعينة واحدة في SPSS وحصلت على النتائج التالية:
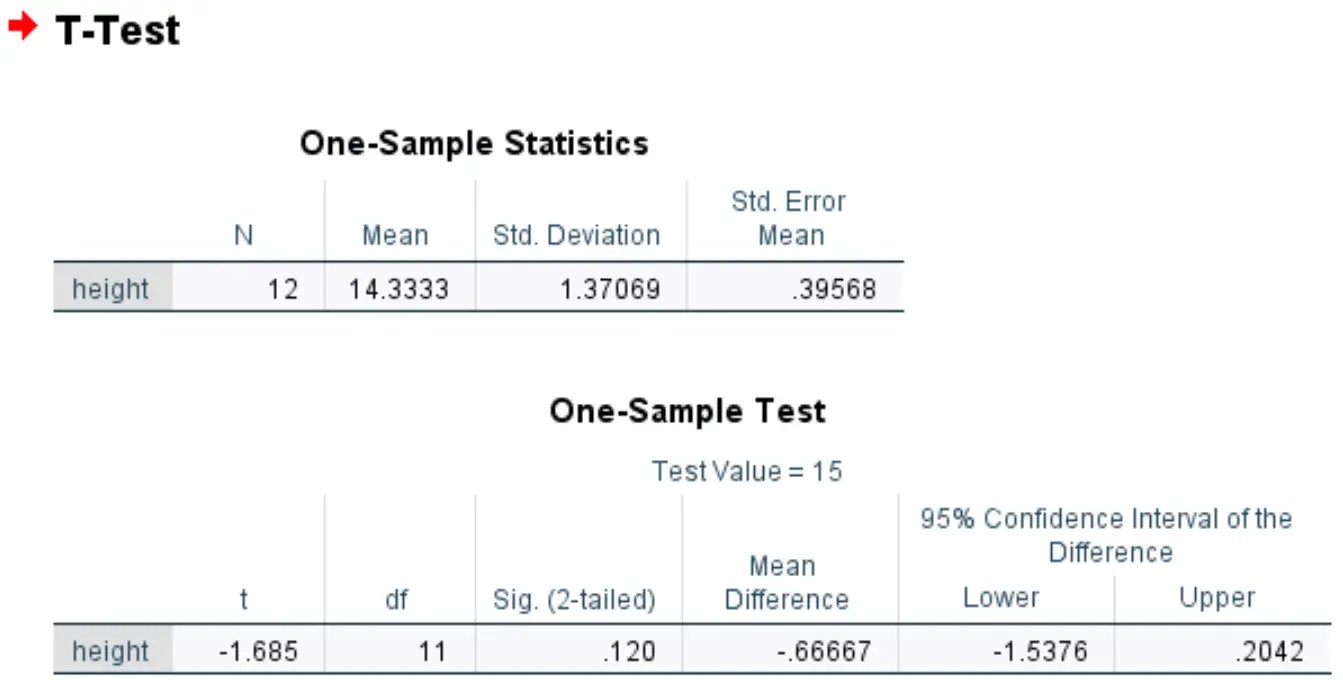
سيج. القيمة (على الوجهين) هي 0.120 .
يمثل هذا القيمة p ذات الوجهين والتي تتوافق مع قيمة -1.685 مع 11 درجة حرية.
وبما أن القيمة p للاختبار (0.120) لا تقل عن 0.05، فإننا نفشل في رفض الفرضية الصفرية.
وبعبارة أخرى، ليس لدينا ما يكفي من الأدلة لنقول أن متوسط الارتفاع الحقيقي لهذا النوع من النباتات هو أي شيء آخر غير 15 بوصة.
مثال 2: اختبار t لعينتين
يتم استخدام اختبار t المكون من عينتين لاختبار ما إذا كانت القيم المتوسطة لمجموعتين من السكان متساوية أم لا.
على سبيل المثال، لنفترض أن الباحثين يريدون معرفة ما إذا كانت المعالجة الجديدة للوقود تؤدي إلى تغيير في متوسط عدد الكيلومترات المقطوعة لكل جالون لسيارة معينة. ولاختبار ذلك، أجروا تجربة حيث تلقت 12 سيارة معالجة الوقود الجديدة و12 سيارة لم تحصل عليها.
يقوم الباحثون بإجراء اختبار t مكون من عينتين مع الفرضيات الصفرية والبديلة التالية:
- H 0 : μ 1 = μ 2 (متوسط ميل لكل جالون بين المجموعتين متساوي)
- H 1 : μ 1 ≠ μ 2 (متوسط ميل لكل جالون بين المجموعتين غير متساوي)
قاموا بإجراء اختبار t من عينتين في برنامج SPSS وحصلوا على النتائج التالية:
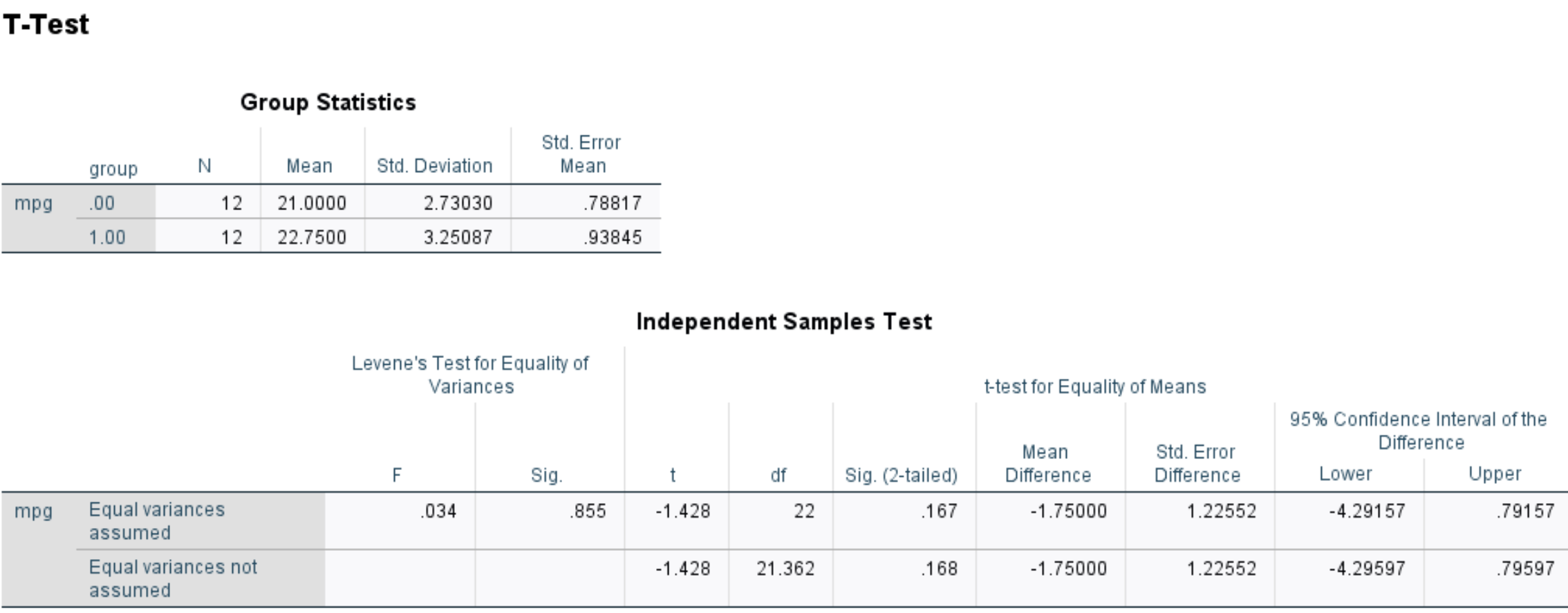
سيج. القيمة (على الوجهين) هي 0.167 .
يمثل هذا القيمة p ثنائية الطرف والتي تتوافق مع قيمة -1.428 مع 22 درجة حرية.
وبما أن القيمة p للاختبار (0.167) لا تقل عن 0.05، فإننا نفشل في رفض الفرضية الصفرية.
وبعبارة أخرى، ليس لدينا ما يكفي من الأدلة لنقول أن المتوسط الحقيقي للميل لكل جالون يختلف بين السيارات التي تتلقى العلاج وتلك التي لا تتلقى العلاج.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إجراء اختبارات إحصائية مختلفة في برنامج SPSS:
كيفية إجراء اختبار t لعينة واحدة في برنامج SPSS
كيفية إجراء اختبار t لعينتين في برنامج SPSS
كيفية إجراء اختبار t للعينات المقترنة في برنامج SPSS
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر