الأحداث الشاملة بشكل جماعي: التعريف والمثال

تعتبر مجموعة الأحداث شاملة بشكل جماعي إذا كان من المتوقع وقوع حدث واحد على الأقل.

على سبيل المثال، إذا قمنا برمي حجر نرد، فيجب أن يستقر على إحدى القيم التالية:

• 1
• 2
• 3
• 4
• 5
• 6

وبالتالي، يمكننا القول أن مجموعة الأحداث {1، 2، 3، 4، 5، 6} شاملة بشكل جماعي لأن حجر النرد يجب أن يستقر على إحدى هذه القيم.

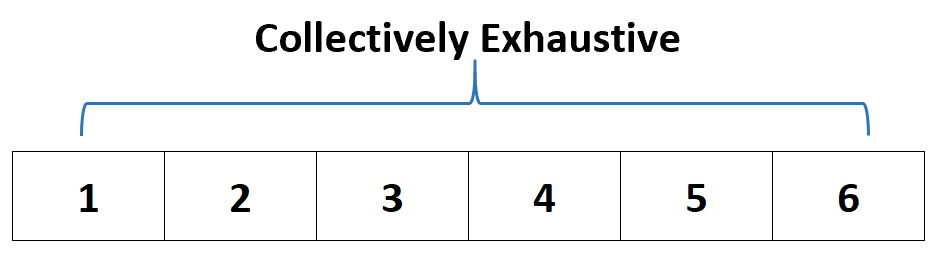
بمعنى آخر، هذه المجموعة من الأحداث، كمجموعة ، تستنفد جميع النتائج المحتملة.

توضح الأمثلة التالية مواقف أخرى توضح أحداثًا شاملة بشكل جماعي:

مثال 1: اقلب عملة معدنية

لنفترض أننا ألقينا قطعة نقود مرة واحدة. نحن نعلم أن العملة يجب أن تهبط على إحدى القيم التالية:

• رؤساء
• ذيول

وبالتالي، فإن مجموعة أحداث {الرأس والذيل} ستكون شاملة بشكل جماعي.

مثال 2: تدوير القمة

لنفترض أن لدينا عجلة روليت بثلاثة ألوان مختلفة: الأحمر والأزرق والأخضر.

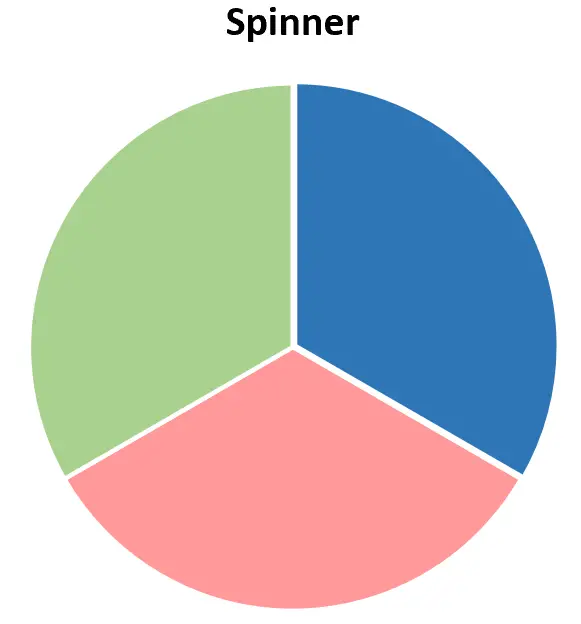
إذا قمنا بتدويرها مرة واحدة فيجب أن تهبط على إحدى القيم التالية:

• أحمر
• أزرق
• أخضر

وبالتالي، فإن مجموعة الأحداث {الأحمر، الأزرق، الأخضر} ستكون شاملة بشكل جماعي.

ومع ذلك، فإن مجموعة الأحداث {أحمر، أخضر} لن تكون شاملة بشكل جماعي لأنها لا تحتوي على جميع النتائج المحتملة.

مثال 3: أنواع لاعبي كرة السلة

لنفترض أن لدينا استبيانًا يطلب من الأفراد اختيار موقعهم المفضل في كرة السلة. الإجابات الوحيدة الممكنة هي:

• زعيم اللعبة
• اطلاق النار على الحارس
• صغير إلى الأمام
• قوة إلى الأمام
• مركز

وبالتالي، فإن مجموعة الأحداث {Point Guard، Shooting Guard، Small Forward، Power Forward، Center} ستكون شاملة بشكل جماعي.

ومع ذلك، فإن مجموعة الأحداث {Point Guard، Shooting Guard، Small Forward} لن تكون شاملة بشكل جماعي لأنها لا تحتوي على جميع النتائج المحتملة.

أهمية الأحداث الشاملة بشكل جماعي في الدراسات الاستقصائية

عند تصميم الدراسات الاستقصائية، من المهم بشكل خاص أن تكون الإجابات على الأسئلة شاملة بشكل جماعي.

على سبيل المثال، لنفترض أن الاستطلاع يطرح السؤال التالي:

ما هو موقفك المفضل في كرة السلة؟

ولنفترض أن الإجابات المحتملة هي:

• زعيم اللعبة
• اطلاق النار على الحارس
• صغير إلى الأمام
• قوة إلى الأمام

ومع ترك موقف الوسط جانباً، فإن هذه الإجابات ليست شاملة بشكل جماعي.

وهذا يعني أن الشخص الذي يفضل المركز باعتباره موقعه المفضل سيتعين عليه اختيار أحد الخيارات الأخرى، مما يعني أن إجابات الاستطلاع لن تعكس الآراء الحقيقية للأشخاص الذين شملهم الاستطلاع.

جماعية شاملة أو حصرية بشكل متبادل

تكون الأحداث متنافية إذا لم يمكن أن تحدث في نفس الوقت.

على سبيل المثال، دع الحدث A هو الحدث الذي يقع فيه حجر النرد على رقم زوجي، وليكن الحدث B هو الحدث الذي يقع فيه حجر النرد على رقم فردي.

ويمكننا تعريف فضاء العينة للأحداث على النحو التالي:

• أ = {2، 4، 6}
• ب = {1، 3، 5}

لاحظ أنه لا يوجد تداخل بين مساحتي العينة، مما يعني أنهما متنافيان. كما أنها تكون شاملة بشكل جماعي لأنها مجتمعة قادرة على حساب جميع النتائج المحتملة لرمية القالب.

ومع ذلك، لنفترض أننا حددنا الحدث A والحدث B على النحو التالي:

• أ = {1، 2، 3، 4}
• ب = {3، 4، 5، 6}

في هذه الحالة، هناك بعض التداخل بين A وB، لذلك لا يستبعد أحدهما الآخر. ومع ذلك، مجتمعة، لا يزال بإمكانهم أن يأخذوا في الاعتبار جميع النتائج المحتملة لرمي القالب.

يوضح هذا نقطة مهمة: يمكن لمجموعة من الأحداث أن تكون شاملة بشكل جماعي دون أن تكون متنافية .