R مقابل r-square: ما الفرق؟

المصطلحان اللذان غالبًا ما يخلطهما الطلاب في الإحصاء هما R و R-squared ، وغالبًا ما يتم كتابتهما ^R2 .

في سياق الانحدار الخطي البسيط :

• ج: العلاقة بين متغير التوقع x ومتغير الاستجابة y.
• ^R2 : نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بواسطة المتغير المتوقع في نموذج الانحدار.

وفي سياق الانحدار الخطي المتعدد :

• ج: العلاقة بين القيم المرصودة لمتغير الاستجابة والقيم المتوقعة لمتغير الاستجابة التي صنعها النموذج.
• ^R2 : نسبة تباين متغير الاستجابة التي يمكن تفسيرها بالمتغيرات التنبؤية لنموذج الانحدار.

لاحظ أن قيمة R ² تقع بين 0 و1. وكلما اقتربت القيمة من 1، زادت قوة العلاقة بين متغير (متغيرات) التوقع ومتغير الاستجابة.

توضح الأمثلة التالية كيفية تفسير قيم R وR-squared في الانحدار الخطي البسيط ونماذج الانحدار الخطي المتعددة.

المثال 1: الانحدار الخطي البسيط

لنفترض أن لدينا مجموعة البيانات التالية التي توضح ساعات الدراسة ودرجات الامتحانات التي حصل عليها 12 طالبًا في دورة معينة في الرياضيات:

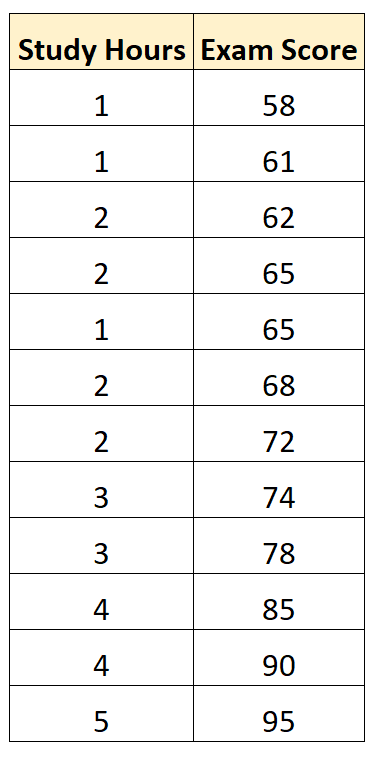
باستخدام البرامج الإحصائية (مثل Excel وR وPython وSPSS وما إلى ذلك)، يمكننا ملاءمة نموذج انحدار خطي بسيط باستخدام “ساعات الدراسة” كمتغير متوقع و”درجة الامتحان” كمتغير استجابة .

يمكننا العثور على الإخراج التالي لهذا النموذج:

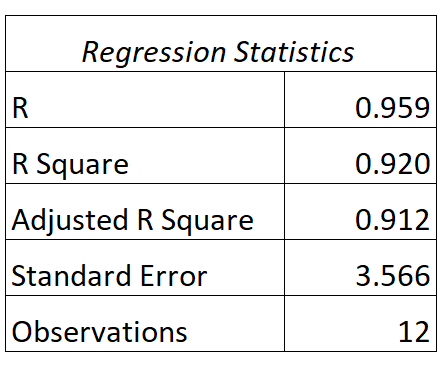
إليك كيفية تفسير قيم R و R التربيعية لهذا النموذج:

• ج: العلاقة بين ساعات الدراسة ودرجة الامتحان هي 0.959 .
• R ² : مربع R لنموذج الانحدار هذا هو 0.920 . وهذا يخبرنا أن 92.0% من التباين في درجات الامتحان يمكن تفسيره بعدد ساعات الدراسة.

لاحظ أيضًا أن قيمة R ² تساوي ببساطة قيمة R مربعة:

^R2 = R * R = 0.959 * 0.959 = 0.920

المثال 2: الانحدار الخطي المتعدد

لنفترض أن لدينا مجموعة البيانات التالية التي توضح عدد الساعات التي تمت دراستها ودرجة الطالب الحالية ودرجة الاختبار التي حصل عليها 12 طالبًا في دورة معينة في الرياضيات:

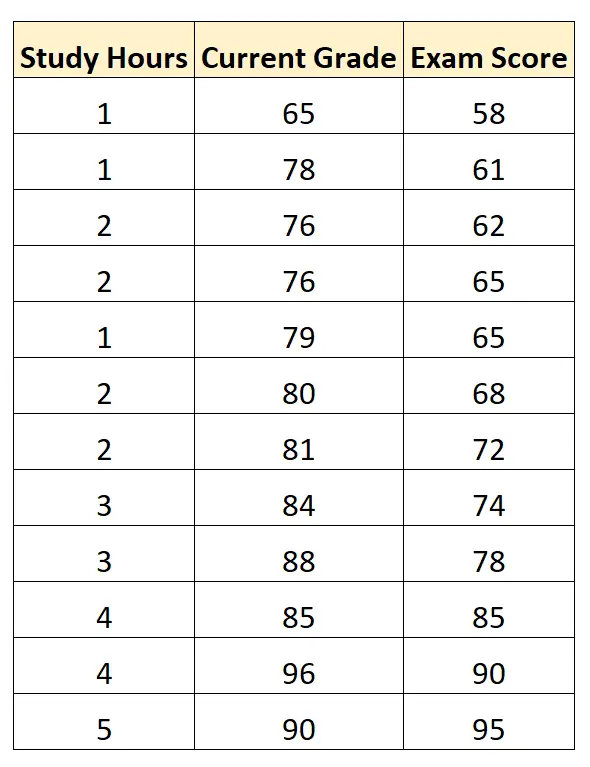
باستخدام البرمجيات الإحصائية، يمكننا ملاءمة نموذج الانحدار الخطي المتعدد باستخدام “ساعات الدراسة” و”الصف الحالي” كمتغيرات متوقعة و”درجة الامتحان” كمتغير الاستجابة.

يمكننا العثور على الإخراج التالي لهذا النموذج:

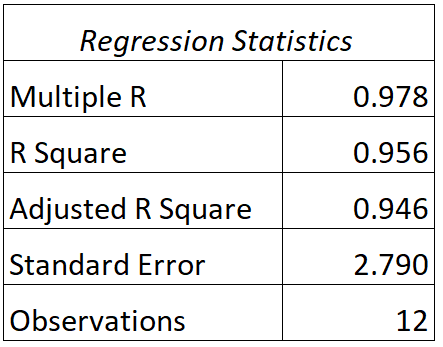
إليك كيفية تفسير قيم R و R التربيعية لهذا النموذج:

• ج: العلاقة بين درجات الاختبار الفعلية ودرجات الاختبار المتوقعة للنموذج هي 0.978 .
• R ² : مربع R لنموذج الانحدار هذا هو 0.956 . وهذا يخبرنا أن 95.6% من التباين في درجات الامتحان يمكن تفسيره بعدد الساعات المدروسة والدرجة الحالية للطالب في الفصل.

لاحظ أيضًا أن قيمة R ² تساوي ببساطة قيمة R مربعة:

^R2 = R * R = 0.978 * 0.978 = 0.956

مصادر إضافية

ما هي قيمة R-squared الجيدة؟
دليل لطيف لمجموع المربعات: SST، SSR، SSE