دليل لطيف لمجموع المربعات: sst، ssr، sse
يتم استخدام الانحدار الخطي للعثور على الخط الذي “يناسب” مجموعة من البيانات بشكل أفضل.
غالبًا ما نستخدم ثلاثة مجموعات مختلفة من قيم المربعات لقياس مدى ملاءمة خط الانحدار للبيانات فعليًا:
1. مجموع المربعات الإجمالية (SST) – مجموع مربعات الاختلافات بين نقاط البيانات الفردية (y i ) ومتوسط متغير الاستجابة ( y ).
- درجة حرارة سطح البحر = Σ(ص ط – ذ ) 2
2. انحدار مجموع المربعات (SSR) – مجموع مربعات الاختلافات بين نقاط البيانات المتوقعة (ŷ i ) ومتوسط متغير الاستجابة ( y ).
- SSR = Σ(ŷ i – y ) 2
3. مجموع مربعات الخطأ (SSE) – مجموع مربعات الاختلافات بين نقاط البيانات المتوقعة (ŷ i ) ونقاط البيانات المرصودة (y i ).
- SSE = Σ(ŷ i – y i ) 2
وتوجد العلاقة التالية بين هذه المقاييس الثلاثة:
طائرة أسرع من الصوت = SSR + SSE
لذا، إذا كنا نعرف اثنين من هذه القياسات، فيمكننا استخدام الجبر البسيط لحساب القياس الثالث.
SSR وSST وR-Square
R-squared ، الذي يُطلق عليه أحيانًا معامل التحديد، هو مقياس لمدى ملاءمة نموذج الانحدار الخطي لمجموعة البيانات. ويمثل نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بواسطة المتغير المتنبئ.
يمكن أن تتراوح قيمة R-squared من 0 إلى 1. وتشير القيمة 0 إلى أنه لا يمكن تفسير متغير الاستجابة بواسطة متغير التوقع على الإطلاق. تشير القيمة 1 إلى أنه يمكن تفسير متغير الاستجابة بشكل مثالي دون أخطاء بواسطة متغير التوقع.
باستخدام SSR وSST، يمكننا حساب مربع R على النحو التالي:
R تربيع = SSR / SST
على سبيل المثال، إذا كان SSR لنموذج انحدار معين هو 137.5 وSST هو 156، فسنحسب مربع R كما يلي:
ر تربيع = 137.5 / 156 = 0.8814
يخبرنا هذا أن 88.14% من التباين في متغير الاستجابة يمكن تفسيره بواسطة المتغير المتنبئ.
حساب SST، SSR، SSE: مثال خطوة بخطوة
لنفترض أن لدينا مجموعة البيانات التالية التي توضح عدد الساعات التي درسها ستة طلاب مختلفين بالإضافة إلى درجات الامتحانات النهائية:
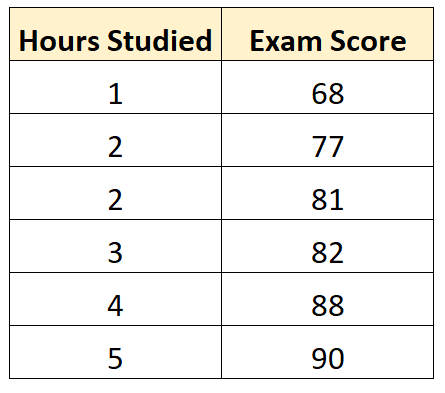
باستخدام بعض البرامج الإحصائية (مثل R و Excel و Python ) أو حتى يدويًا، يمكننا أن نرى أن الخط الأنسب هو:
النتيجة = 66.615 + 5.0769*(ساعات)
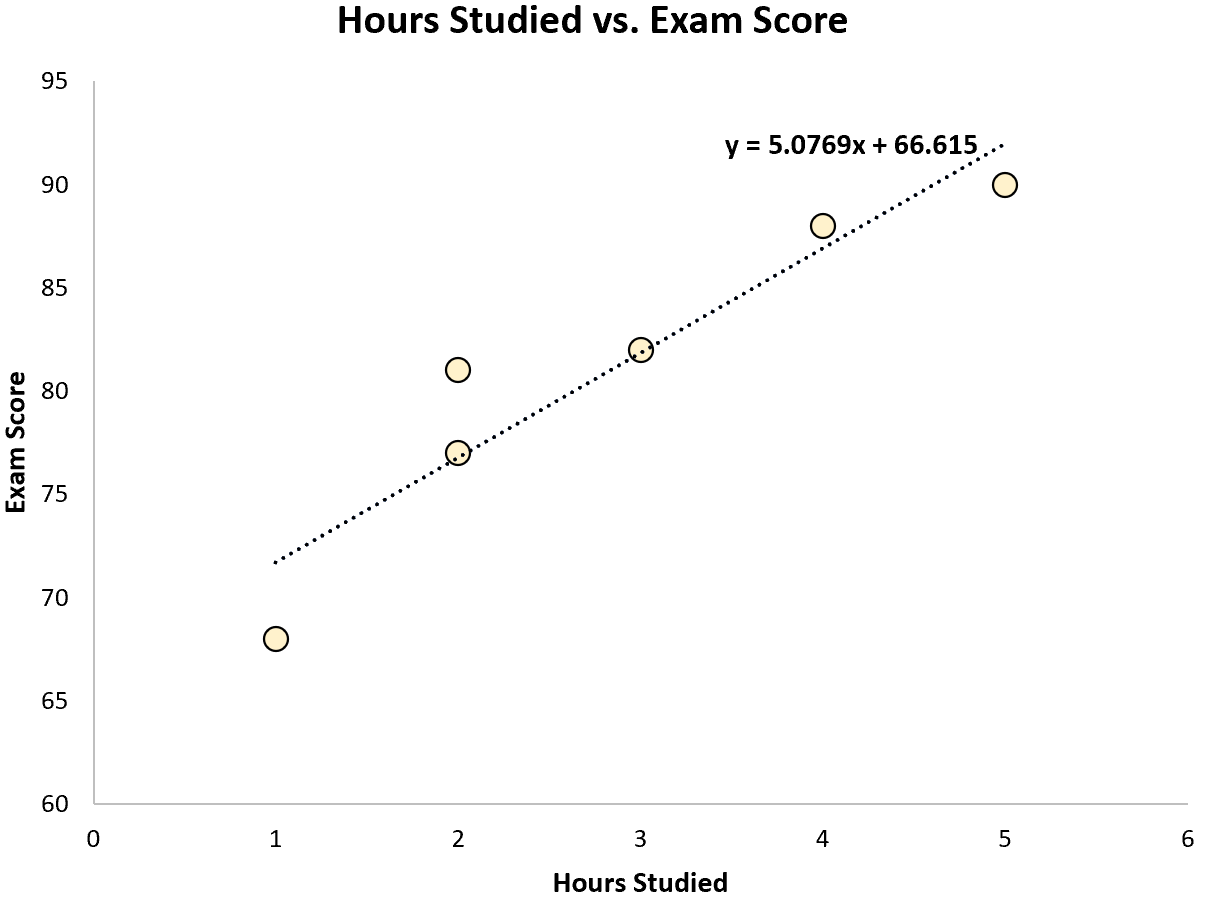
بمجرد أن نعرف خط المعادلة الأكثر ملائمة، يمكننا استخدام الخطوات التالية لحساب SST وSSR وSSE:
الخطوة 1: حساب متوسط متغير الاستجابة.
متوسط متغير الاستجابة ( y ) يساوي 81 .
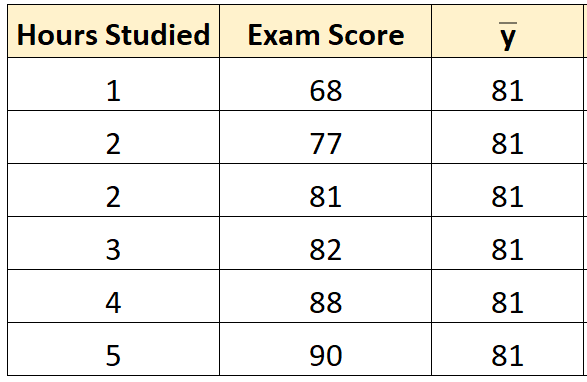
الخطوة 2: احسب القيمة المتوقعة لكل ملاحظة.
ثم يمكننا استخدام خط المعادلة الأنسب لحساب درجة الاختبار المتوقعة () لكل طالب.
على سبيل المثال درجة الامتحان المتوقعة للطالب الذي درس ساعة واحدة هي:
النتيجة = 66.615 + 5.0769*(1) = 71.69 .
يمكننا استخدام نفس الطريقة للعثور على النتيجة المتوقعة لكل طالب:
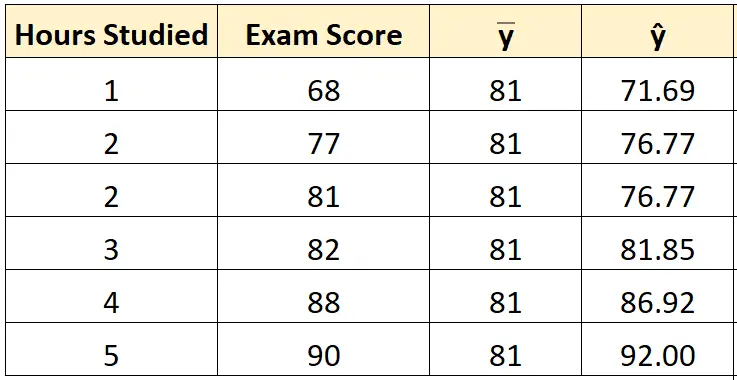
الخطوة 3: حساب مجموع المربعات (SST).
ثم يمكننا حساب مجموع المربعات في المجموع.
على سبيل المثال، مجموع المربعات للطالب الأول هو:
(y i – y ) 2 = (68 – 81) 2 = 169 .
يمكننا استخدام نفس الطريقة للعثور على مجموع المربعات لكل طالب:
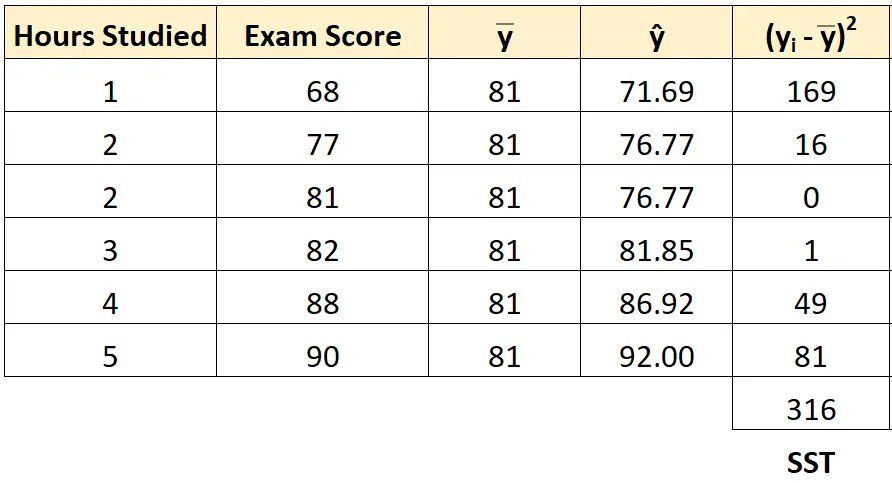
المجموع الكلي للمربعات تبين أنه 316 .
الخطوة 4: حساب مجموع انحدار المربعات (SSR).
ثم يمكننا حساب مجموع انحدار المربعات.
على سبيل المثال، مجموع انحدار المربعات للطالب الأول هو:
( ŷi – y ) 2 = (71.69 – 81) 2 = 86.64 .
يمكننا استخدام نفس الطريقة للعثور على انحدار مجموع المربعات لكل طالب:
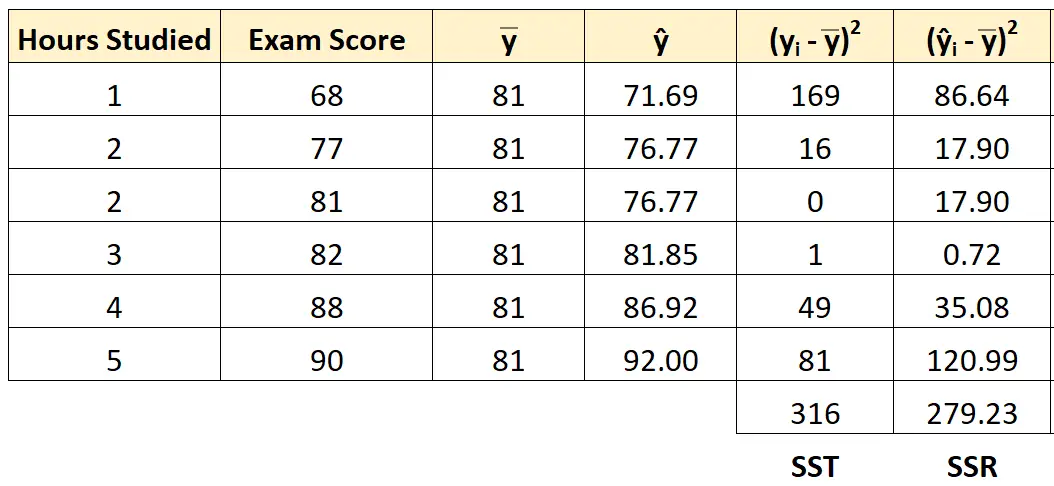
تبين أن مجموع انحدار المربعات هو 279.23 .
الخطوة 5: حساب مجموع مربعات الخطأ (SSE).
ثم يمكننا حساب خطأ مجموع المربعات.
على سبيل المثال، مجموع مربعات الخطأ للطالب الأول هو:
(ŷ i – y i ) 2 = (71.69 – 68) 2 = 13.63 .
يمكننا استخدام نفس الطريقة للعثور على مجموع مربعات الخطأ لكل طالب:
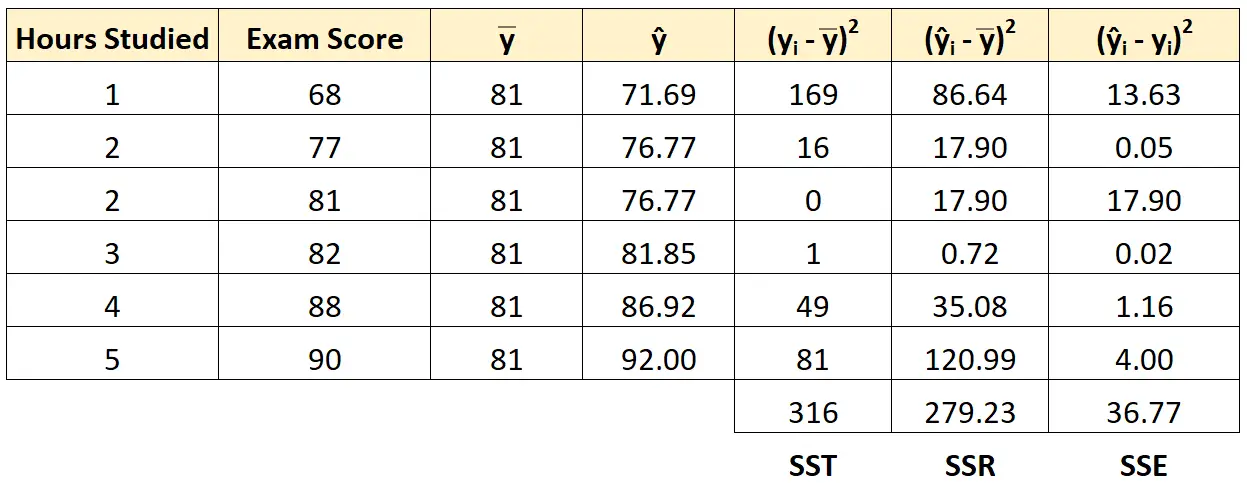
يمكننا التحقق من أن SST = SSR + SSE
- طائرة أسرع من الصوت = SSR + SSE
- 316 = 279.23 + 36.77
يمكننا أيضًا حساب مربع R لنموذج الانحدار باستخدام المعادلة التالية:
- R تربيع = SSR / SST
- ر تربيع = 279.23 / 316
- ر تربيع = 0.8836
وهذا يخبرنا أن 88.36% من التباين في درجات الامتحان يمكن تفسيره بعدد ساعات الدراسة.
مصادر إضافية
يمكنك استخدام الآلات الحاسبة التالية لحساب SST وSSR وSSE تلقائيًا لأي خط انحدار خطي بسيط:
آلة حاسبة SST
حاسبة آر إس إس
حاسبة ESS
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر