كيفية إجراء تحليل التباين أحادي الاتجاه في برنامج spss

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

يُطلق على هذا النوع من الاختبارات اسم ANOVA أحادي الاتجاه لأننا نقوم بتحليل تأثير متغير التوقع على متغير الاستجابة.

إذا كنا مهتمين بدلاً من ذلك بتأثير متغيرين متوقعين على متغير الاستجابة، فيمكننا إجراء تحليل التباين (ANOVA) ثنائي الاتجاه .

يشرح هذا البرنامج التعليمي كيفية إجراء تحليل التباين (ANOVA) أحادي الاتجاه في برنامج SPSS.

مثال: تحليل التباين أحادي الاتجاه في SPSS

لنفترض أن أحد الباحثين قام بتجنيد 30 طالبًا للمشاركة في إحدى الدراسات. يتم تعيين الطلاب بشكل عشوائي لاستخدام إحدى تقنيات الدراسة الثلاثة في الشهر التالي للتحضير للامتحان. وفي نهاية الشهر، يقوم جميع الطلاب بإجراء نفس الاختبار.

تظهر نتائج اختبار الطلاب أدناه:

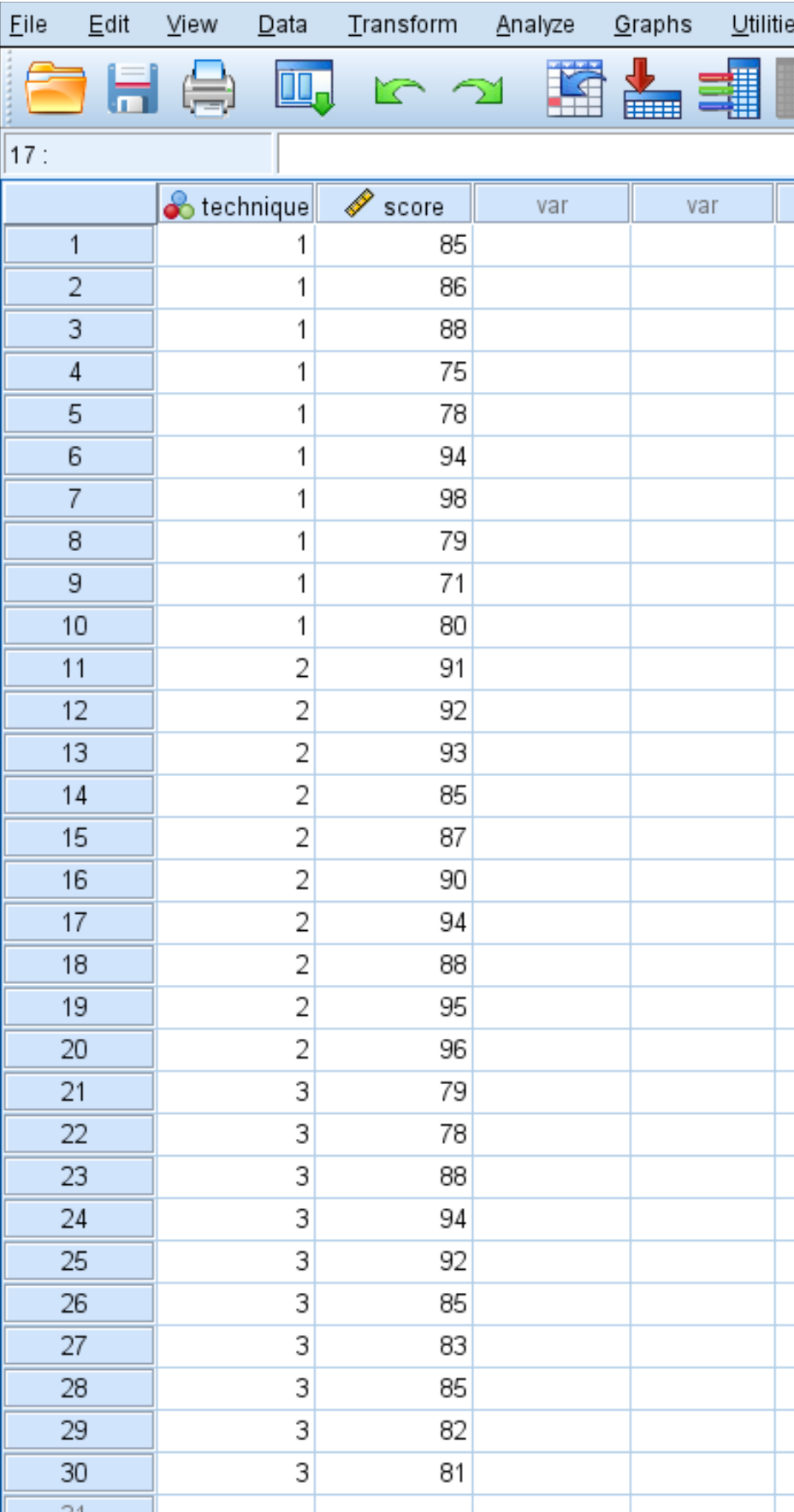
استخدم الخطوات التالية لإجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كانت الدرجات المتوسطة هي نفسها عبر المجموعات الثلاث.

الخطوة 1: تصور البيانات.

أولاً، سنقوم بإنشاء مخططات مربعة لتصور توزيع درجات الاختبار لكل من تقنيات الدراسة الثلاثة. انقر فوق علامة التبويب “المخططات” ، ثم انقر فوق “منشئ المخططات” .

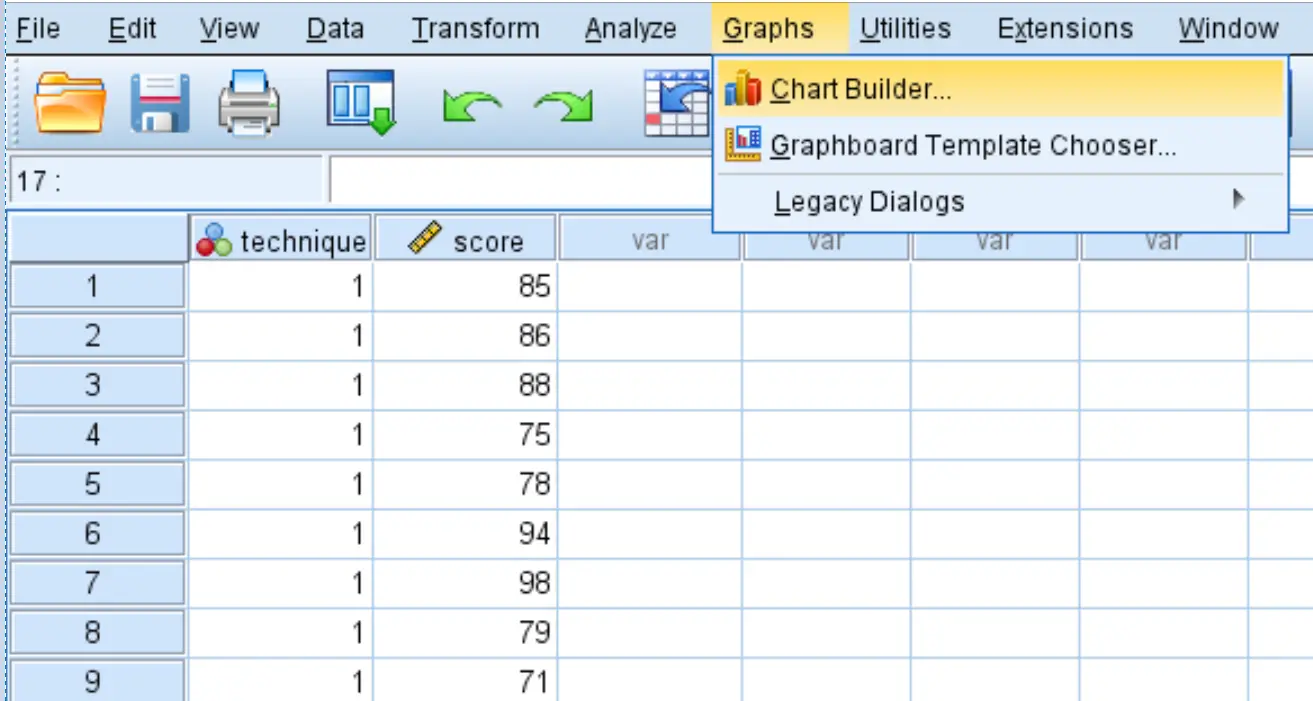
حدد Boxplot في نافذة الاختيار من:. ثم اسحب المخطط الأول المسمى Simple boxplot إلى نافذة التحرير الرئيسية. اسحب المتغير الفني على المحور السيني والنتيجة على المحور الصادي.

ثم انقر فوق “خصائص العنصر” ، ثم انقر فوق “المحور Y1” . قم بتغيير الحد الأدنى للقيمة إلى 60. ثم انقر فوق “موافق” .

سوف تظهر boxplots التالية:

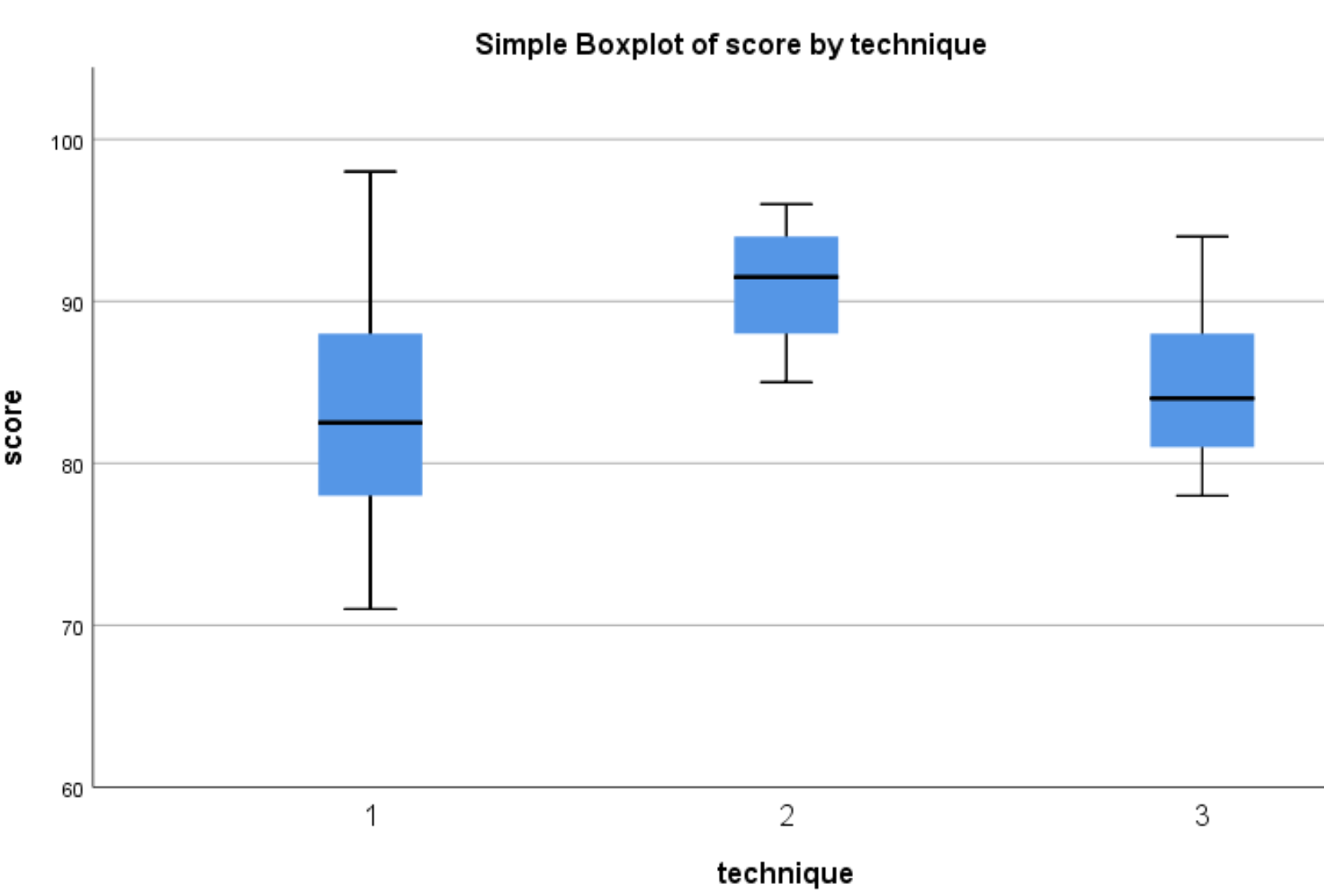
يمكننا أن نرى أن توزيع درجات الاختبار يميل إلى أن يكون أعلى بالنسبة للطلاب الذين استخدموا التقنية 2 مقارنةً بالطلاب الذين استخدموا التقنيتين 1 و3. ولتحديد ما إذا كانت فروق الدرجات هذه ذات دلالة إحصائية، سنقوم بإجراء تحليل التباين (ANOVA) أحادي الاتجاه.

الخطوة 2: إجراء تحليل التباين (ANOVA) في اتجاه واحد.

انقر فوق علامة التبويب تحليل ، ثم مقارنة الوسائل ، ثم تحليل التباين أحادي الاتجاه .

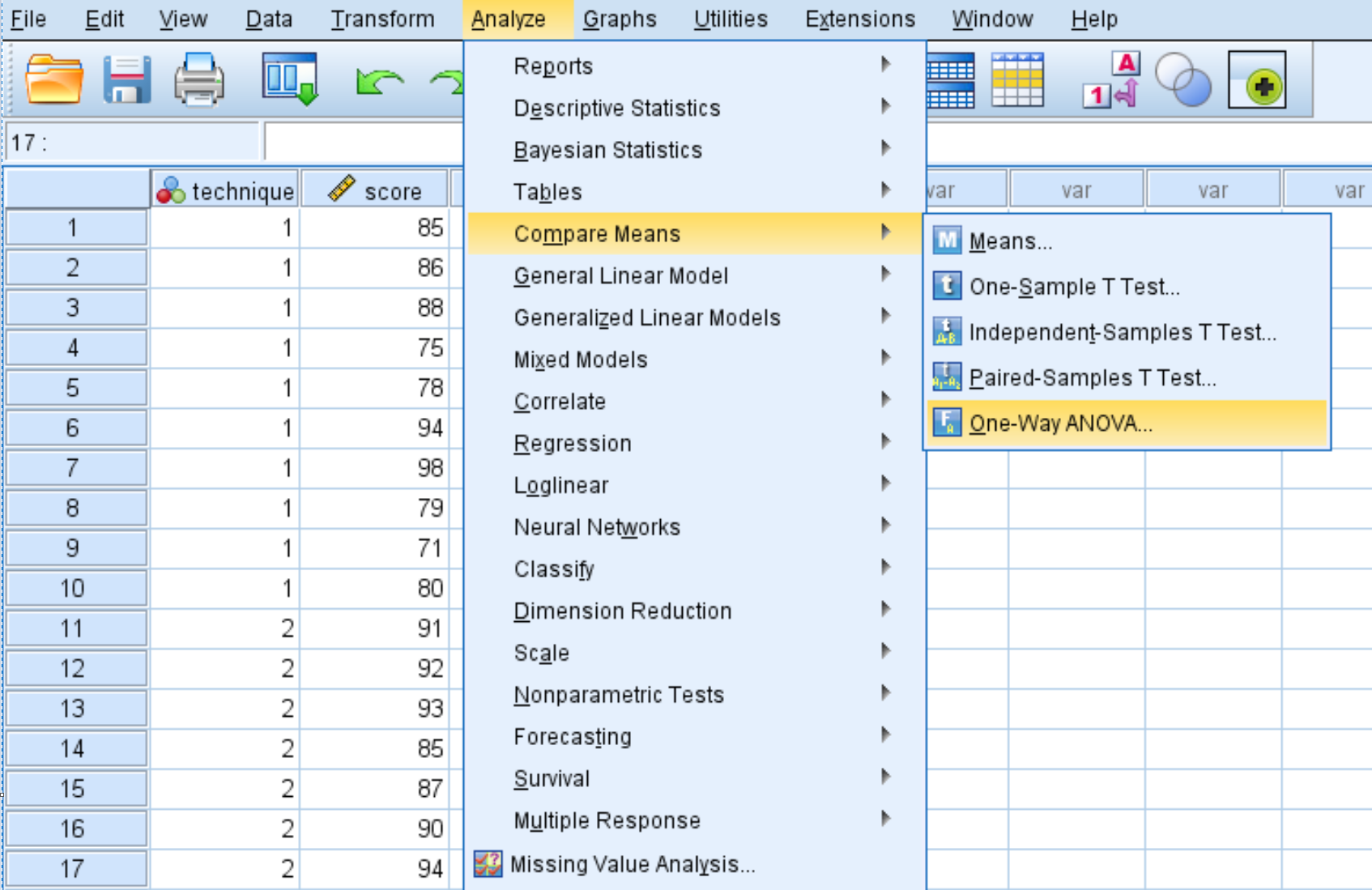
في النافذة الجديدة التي تظهر، ضع درجة المتغير في المربع المسمى قائمة التابعين وتقنية المتغير في المربع المسمى العامل.

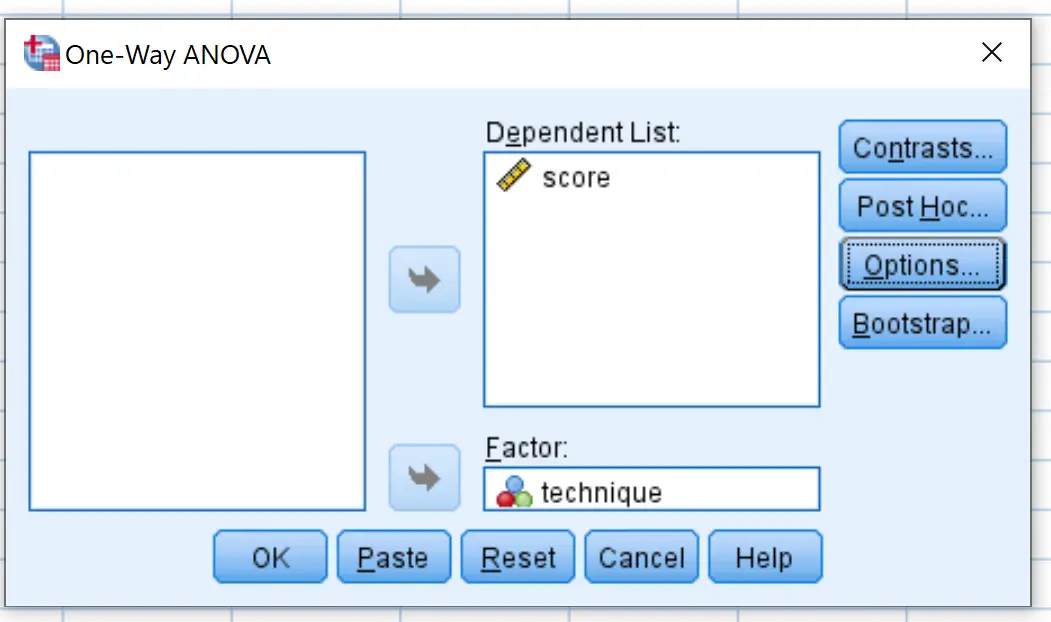
ثم انقر فوق Post Hoc وحدد المربع الموجود بجوار Tukey . ثم انقر فوق “متابعة” .

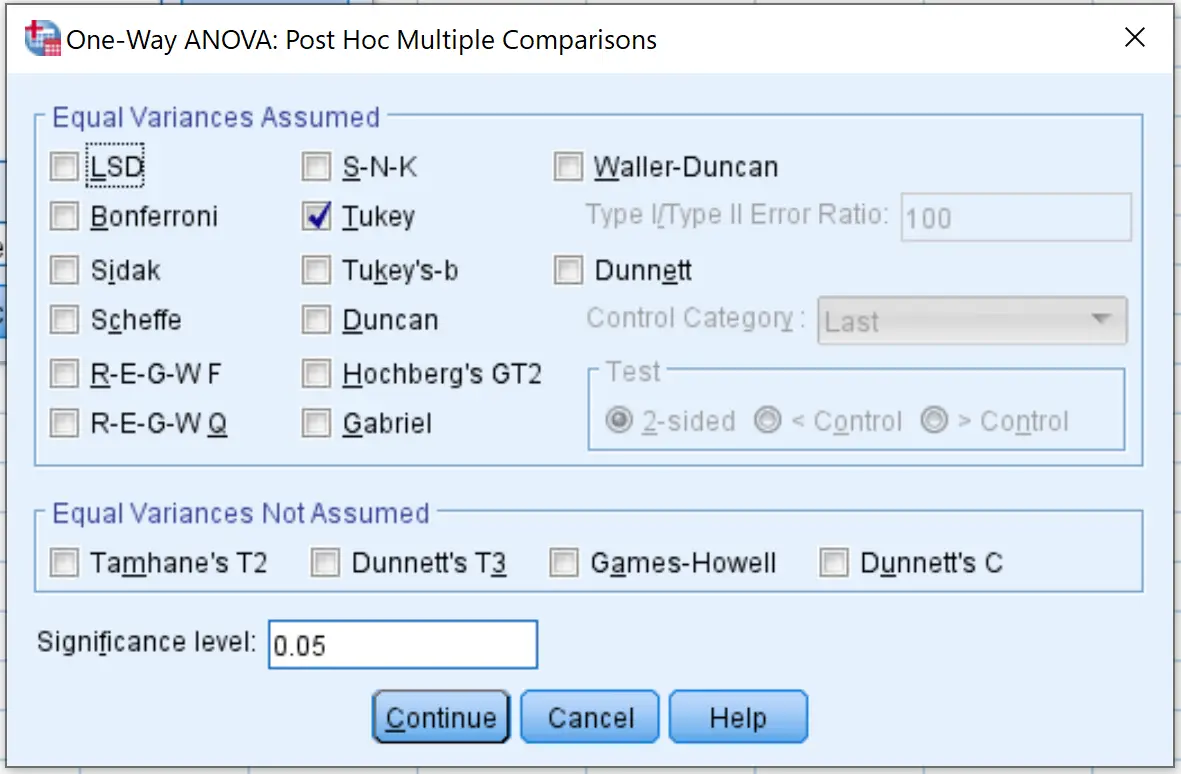
ثم انقر فوق “خيارات” وحدد المربع الموجود بجوار “وصفي” . ثم انقر فوق “متابعة” .

وأخيرا، انقر فوق موافق .

الخطوة 3: تفسير النتيجة.

بمجرد النقر فوق “موافق” ، ستظهر نتائج ANOVA أحادية الاتجاه. وإليك كيفية تفسير النتيجة:

وصف الجدول

يعرض هذا الجدول إحصائيات وصفية لكل مجموعة من المجموعات الثلاث في مجموعة البيانات الخاصة بنا.

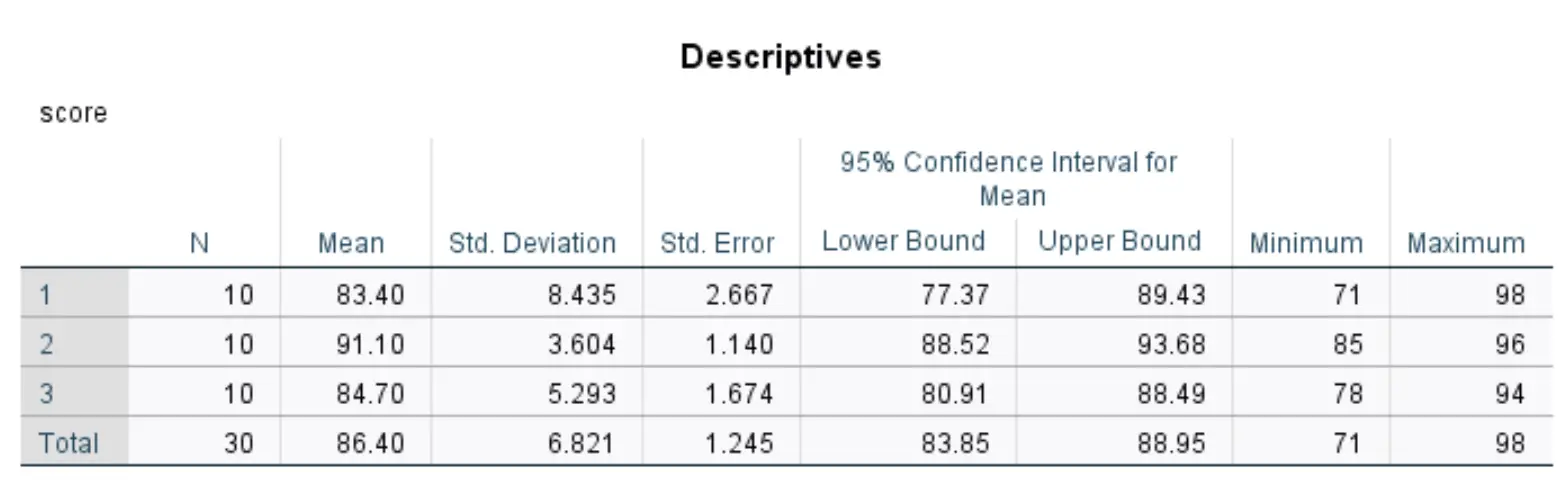
تشمل الأرقام الأكثر صلة ما يلي:

• N: عدد الطلاب في كل مجموعة.
• المتوسط: متوسط درجات الاختبار لكل مجموعة.
• معيار. الانحراف: الانحراف المعياري لنتائج الاختبار لكل مجموعة.

جدول أنوفا

يعرض هذا الجدول نتائج تحليل التباين الأحادي:

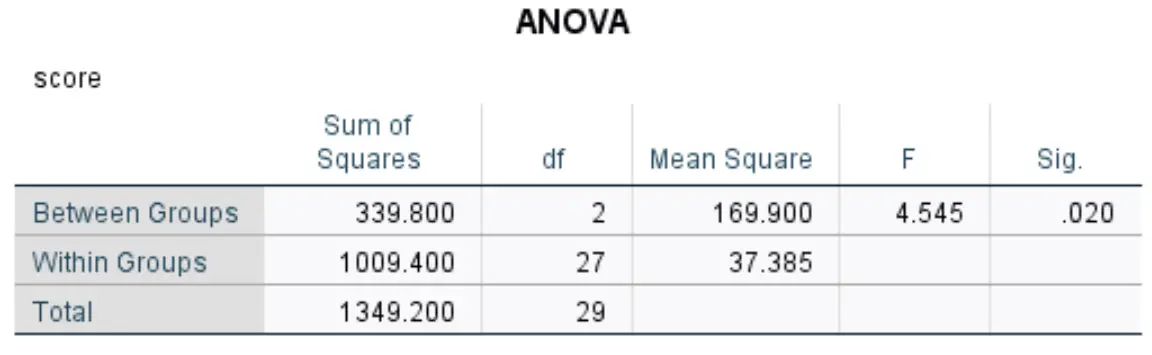
تشمل الأرقام الأكثر صلة ما يلي:

• F: إحصائية F الشاملة.
• Sig: القيمة p التي تتوافق مع إحصائية F (4.545) مع البسط df (2) والمقام df (27). في هذه الحالة، القيمة p هي 0.020 .

تذكر أن تحليل التباين أحادي الاتجاه يستخدم الفرضيات الصفرية والبديلة التالية:

• H ₀ (فرضية العدم): μ ₁ = μ ₂ = μ ₃ = … = μ _k (جميع الوسائل السكانية متساوية)
• _HA (فرضية بديلة): هناك متوسط سكاني واحد على الأقل مختلف   استراحة

نظرًا لأن القيمة p لجدول ANOVA أقل من 0.05، فلدينا أدلة كافية لرفض فرضية العدم واستنتاج أن إحدى وسائل المجموعة على الأقل تختلف عن الوسائل الأخرى.

لمعرفة بالضبط أي مجموعة تختلف عن بعضها البعض، يمكننا الرجوع إلى الجدول الأخير لنتيجة ANOVA.

جدول المقارنة المتعددة

يعرض هذا الجدول مقارنات توكي المتعددة اللاحقة بين كل مجموعة من المجموعات الثلاث. نحن مهتمون بشكل أساسي بـ Sig. العمود الذي يعرض القيم p للاختلافات في المتوسطات بين كل مجموعة:

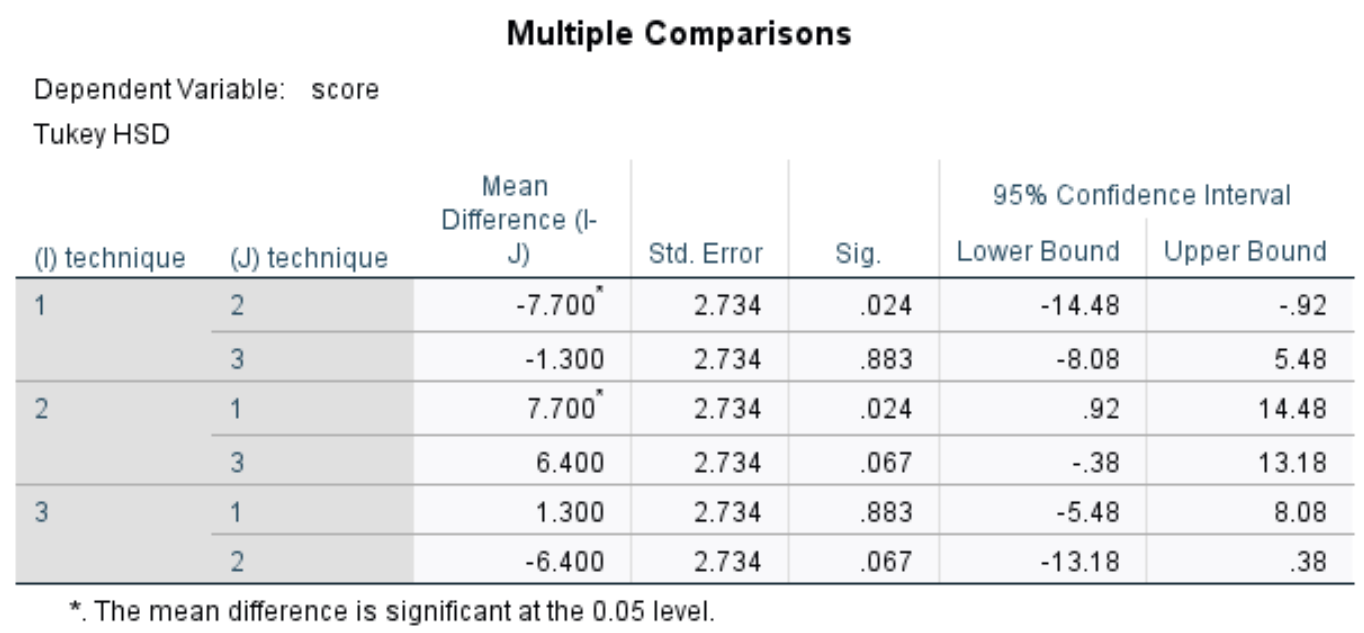
في الجدول يمكننا أن نرى القيم الاحتمالية للمقارنات التالية:

• التقنية 1 مقابل 2: | القيمة p = 0.024
• تقنية 1 ضد 3 | القيمة p = 0.883
• تقنية 2 ضد 3 | القيمة p = 0.067

المقارنة الجماعية الوحيدة ذات القيمة p أقل من 0.05 هي بين التقنية 1 والتقنية 2.

يخبرنا هذا أن هناك فرقًا ذو دلالة إحصائية في متوسط درجات الاختبار بين الطلاب الذين استخدموا التقنية 1 وأولئك الذين استخدموا التقنية 2.

ومع ذلك، لا يوجد فرق ذو دلالة إحصائية بين التقنيات 1 و 3، ولا بين التقنيات 2 و 3.

الخطوة 4: الإبلاغ عن النتائج.

وأخيرا، يمكننا الإبلاغ عن نتائج تحليل التباين الأحادي. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء ANOVA أحادي الاتجاه لتحديد ما إذا كانت ثلاث تقنيات دراسة مختلفة أدت إلى نتائج اختبار مختلفة.

استخدم إجمالي 10 طلاب كلًا من تقنيات الدراسة الثلاثة لمدة شهر قبل إجراء الاختبار نفسه.

كشفت ANOVA أحادية الاتجاه أن هناك فرقًا يعتد به إحصائيًا في درجات الاختبار بين مجموعتين على الأقل (F(2، 27) = 4.545، p = 0.020).

كشف اختبار توكي للمقارنات المتعددة أن متوسط درجات الاختبار كانت مختلفة بشكل كبير بين الطلاب الذين استخدموا التقنية 1 والتقنية 2 (ع = 0.024، 95٪ CI = [-14.48، -0.92]).

لم يكن هناك فرق ذو دلالة إحصائية بين درجات التقنيات 1 و 3 (ع = 0.883) أو بين درجات التقنيات 2 و 3 (ع = 0.067).