كيفية إجراء anova أحادي الاتجاه في excel

يتم استخدام ANOVA أحادي الاتجاه (“تحليل التباين”) لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

يشرح هذا البرنامج التعليمي كيفية إجراء ANOVA أحادي الاتجاه في Excel.

مثال: تحليل التباين أحادي الاتجاه في Excel

لنفترض أن أحد الباحثين قام بتجنيد 30 طالبًا للمشاركة في إحدى الدراسات. يتم تعيين الطلاب بشكل عشوائي لاستخدام إحدى تقنيات الدراسة الثلاثة خلال الأسابيع الثلاثة القادمة للتحضير للامتحان. وفي نهاية الأسابيع الثلاثة، يخضع جميع الطلاب لنفس الاختبار.

تظهر نتائج اختبار الطلاب أدناه:

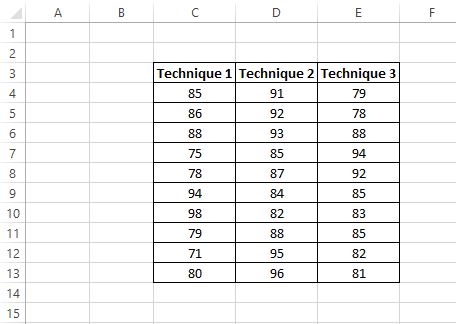
يريد الباحث إجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كانت الدرجات المتوسطة هي نفسها في المجموعات الثلاث.

لإجراء ANOVA أحادي الاتجاه في Excel، انتقل إلى علامة التبويب “بيانات” ، ثم انقر فوق خيار تحليل البيانات في مجموعة التحليل .

إذا كنت لا ترى خيار تحليل البيانات ، فيجب عليك أولاً تحميل برنامج Analysis ToolPak المجاني.

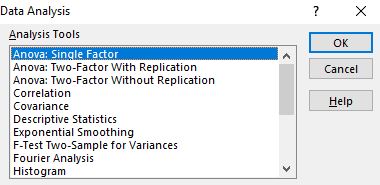
بمجرد النقر عليها، ستظهر نافذة بها خيارات مختلفة لأداة الفحص. حدد Anova: Single Factor ، ثم انقر فوق OK .

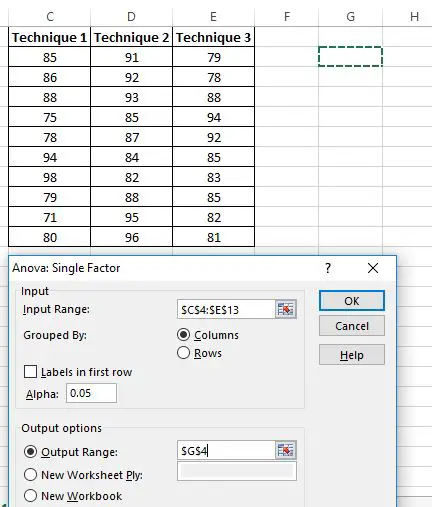
تظهر نافذة جديدة تطلب نطاق الإدخال . يمكنك إما سحب مربع حول بياناتك أو إدخال نطاق البيانات يدويًا. في هذه الحالة، بياناتنا موجودة في الخلايا C4:E13 .

بعد ذلك، اختر مستوى ألفا للاختبار. بشكل افتراضي، هذا الرقم هو 0.05. في هذه الحالة، سأتركها عند 0.05.

أخيرًا، اختر خلية لنطاق الإخراج ، حيث ستظهر نتائج ANOVA أحادية الاتجاه. في هذه الحالة، اخترت الخلية G4 .

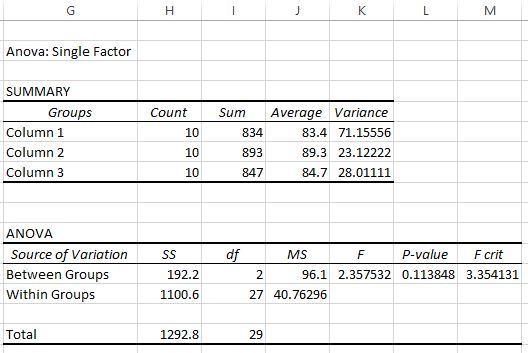
بمجرد النقر فوق “موافق” ، ستظهر نتيجة ANOVA أحادية الاتجاه:

تفسير النتيجة

يتم عرض جدولين في الإخراج. الأول عبارة عن جدول ملخص يوضح عدد درجات الاختبار في كل مجموعة، ومجموع درجات الاختبار، ومتوسط درجات الاختبار، وتباين درجات الاختبار.

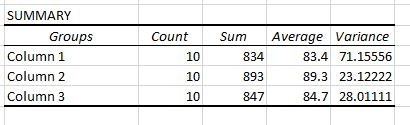
تذكر أنه يتم استخدام تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات أو أكثر أم لا.

من هذا الجدول الأول يمكننا أن نرى أن متوسط الدرجات لكل مجموعة من المجموعات الثلاث يختلف، ولكن لمعرفة ما إذا كانت هذه الاختلافات ذات دلالة إحصائية نحتاج إلى النظر إلى الجدول الثاني.

ويبين الجدول الثاني إحصائية اختبار F وقيمة F الحرجة وقيمة p:

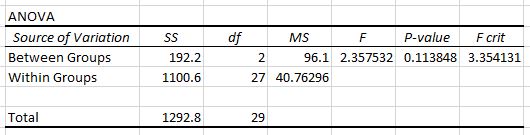
في هذه الحالة، تكون إحصائيات اختبار F هي 2.3575 والقيمة الحرجة لـ F هي 3.3541 . نظرًا لأن إحصائية اختبار F أقل من القيمة الحرجة لـ F، فليس لدينا أدلة كافية لرفض الفرضية الصفرية القائلة بأن متوسطات المجموعات الثلاث متساوية.

وهذا يعني أنه ليس لدينا أدلة كافية لنقول بوجود اختلاف في نتائج الاختبار بين تقنيات الدراسة الثلاثة.

يمكننا أيضًا استخدام القيمة p للوصول إلى نفس النتيجة. في هذه الحالة، القيمة p هي 0.1138 ، وهي أعلى من مستوى ألفا البالغ 0.05 .

وهذا يعني أنه ليس لدينا أدلة كافية لرفض الفرضية الصفرية القائلة بأن متوسطات المجموعات الثلاث متساوية.

ملحوظة: في الحالات التي ترفض فيها فرضية العدم، يمكنك إجراء اختبار Tukey-Kramer اللاحق لتحديد متوسطات المجموعة المختلفة تمامًا.