عينة عشوائية بسيطة
ستتعرف في هذه المقالة على ما هي العينة العشوائية البسيطة وما هي أنواع العينات العشوائية البسيطة الموجودة. بالإضافة إلى ذلك، نوضح كيفية إجراء أخذ العينات العشوائية البسيطة من خلال مثال. وأخيرا، سوف تكون قادرا على معرفة ما هي مزايا وعيوب أخذ العينات العشوائية البسيطة.
ما هو أخذ العينات العشوائية البسيطة؟
في الإحصاء، أخذ العينات العشوائية البسيطة هو أسلوب احتمالي يستخدم لاختيار العينة للدراسة. السمة الرئيسية للعينة العشوائية البسيطة هي أنها تعطي كل عنصر من عناصر المجتمع الإحصائي نفس احتمالية إدراجه في العينة المدروسة.
في العينة العشوائية البسيطة، يتم اختيار عناصر العينة عشوائيا، وبالتالي تكون العينة الناتجة عشوائية تماما.
ولذلك، باستخدام العينة العشوائية البسيطة، فإن احتمال الحصول على عينة معينة يساوي احتمالات الحصول على أي عينة أخرى. وسنرى أدناه كيفية حساب هذا الاحتمال.
ضع في اعتبارك أن هناك طرقًا أخرى لاختيار الأفراد من العينة. أكثر أنواع أخذ العينات استخداماً هي بشكل رئيسي:
- عينة عشوائية بسيطة
- اخذ العينات الطبقية
- أخذ العينات المنهجية
- أخذ العينات العنقودية
من المؤكد أن مفهوم أخذ العينات العشوائية البسيطة هو النوع الأسهل للفهم، ولكن في بعض الأحيان يتبين أنه الأكثر تعقيدًا في التنفيذ، وذلك على وجه التحديد بسبب طبيعته العشوائية.
كيفية القيام بالعينة العشوائية البسيطة
فيما يلي خطوات إجراء أخذ العينات العشوائية البسيطة:
- قم بعمل قائمة بجميع عناصر السكان.
- قم بتعيين رقم تسلسلي (1، 2، 3،…، ن) لكل عنصر في المجتمع.
- ضبط حجم العينة المطلوب.
- استخدم منشئ أرقام عشوائية لإنشاء أكبر عدد ممكن من الأرقام حسب حجم العينة الذي تم اختياره.
- الأفراد المعينون للأرقام التي تم إنشاؤها هم أولئك الذين تم اختيارهم ليكونوا جزءًا من العينة.
هناك عدة طرق لتوليد أرقام عشوائية، أكثرها تقليدية هي طريقة اليانصيب وطريقة جدول الأرقام:
- تتضمن طريقة اليانصيب وضع جميع الأرقام في صندوق، وخلطها ثم سحب الأرقام بشكل عشوائي.
- تتضمن طريقة جدول الأرقام اختيار أرقام عشوائيًا من جدول يحتوي على جميع الأرقام الممكنة.
على الرغم من أنه يمكنك أيضًا استخدام أي من الطريقتين السابقتين، إلا أنهما يتطلبان مزيدًا من الوقت وهما أكثر ملاءمة لأحجام العينات الأصغر. حاليا، يتم استخدام برامج الكمبيوتر لتوليد أرقام عشوائية بشكل أسرع، على سبيل المثال يمكنك استخدام برنامج Excel.
ومن ناحية أخرى، يجب أن تأخذ في الاعتبار أن حجم العينة يجب أن يكون كافيا، حتى يكون هناك أقل خطأ ممكن في أخذ العينات. العثور على حجم العينة المثالي ليس بالأمر السهل؛ إذا كان لديك أي شكوك حول هذا الأمر، يمكنك البحث في موقعنا عن المقالة التي نشرح فيها كيفية القيام بذلك.
مثال لأخذ عينات عشوائية بسيطة
وبمجرد أن نرى تعريف أخذ العينات العشوائية البسيطة، سنرى مثالاً محلولاً لكيفية إجراء هذا النوع من أخذ العينات.
على سبيل المثال، إذا كان هناك 2000 عامل في شركة ما وأردنا إجراء دراسة إحصائية على عينة مكونة من 400 عامل، لاختيار الأفراد الذين سيكونون جزءًا من العينة باستخدام عينة عشوائية بسيطة، فإن أول ما يجب فعله يتكون من – تخصيص رقم لكل موظف من 1 إلى 2000.
بعد تعيين الأرقام، نحتاج إلى اختيار 400 رقم بشكل عشوائي. في هذه الحالة، يكون حجم العينة كبيرًا جدًا، لذا من الأفضل استخدام برامج الكمبيوتر مثل Excel.
وبعد ذلك، سيكون العمال الـ 400 الذين تم اختيارهم للمشاركة في الدراسة هم الذين تم تحديد عددهم في الخطوة السابقة.
في هذا المثال، تم اعتبار 400 عنصر بمثابة حجم عينة تمثيلي بشكل كافٍ، ولكن من المنطقي أن يتغير هذا العدد اعتمادًا على التجربة.
أنواع أخذ العينات العشوائية البسيطة
هناك نوعان من العينات العشوائية البسيطة:
- أخذ العينات العشوائية البسيطة مع الاستبدال : يتم إرجاع العنصر المحدد في إطار أخذ العينات ويمكن اختياره مرة أخرى.
- أخذ العينات العشوائية البسيطة بدون استبدال : يتم حذف العنصر المحدد ليكون جزءًا من العينة ولم يعد من الممكن تحديده.
أخذ العينات العشوائية البسيطة مع الاستبدال هو أبسط نوع من أخذ العينات، حيث يتم تكرار نفس العملية دائمًا لتحديد عنصر من العينة. ومع ذلك، فإن أخذ العينات العشوائية البسيطة بدون استبدال يستخدم على نطاق أوسع لأنه أكثر دقة. يتم شرح كلا النوعين بمزيد من التفاصيل أدناه.
أخذ العينات العشوائية البسيطة مع الإحلال
يتضمن أخذ العينات العشوائية البسيطة مع الاستبدال إعادة كل عنصر محدد إلى إطار أخذ العينات بحيث تكون إمكانية اختياره مرة أخرى موجودة.
لذلك، من الممكن الحصول على عينة تحتوي على عنصر واحد تم اختياره عدة مرات، على الرغم من أن هذا غير مرجح للغاية.
من الناحية الرياضية، يعد هذا نوعًا بسيطًا جدًا من أخذ العينات نظرًا لأن احتمالات كل عملية استخراج هي نفسها. ولهذا السبب من المعتاد البدء بدراسة تقنية أخذ العينات هذه قبل الآخرين.
في أخذ العينات العشوائية البسيطة مع الاستبدال يمكن حساب احتمال الحصول على عينة بترتيب معين باستخدام الصيغة التالية:
![]()
يكون
![]()
العدد الإجمالي لعناصر السكان و
![]()
عدد عمليات الاستخراج المستقلة التي سيتم تنفيذها.
ومن ناحية أخرى، عندما لا يكون الترتيب مهما، يتم حساب احتمال الحصول على العينة باستخدام التعبير التالي:
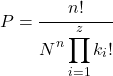
ذهب
![]()
هو عدد عمليات الاستخراج المستقلة،
![]()
عدد العناصر المختلفة في العينة و
![]()
كم مرة تريد ظهور العنصر
![]()
في العينة.
وأخيرا، للعثور على احتمال إدراج العنصر
![]()
، وهذا يعني احتمال تضمين العنصر
![]()
في المثال، ينبغي استخدام الصيغة التالية:
![]()
أخذ عينات عشوائية بسيطة بدون إحلال
يتضمن أخذ العينات العشوائية البسيطة بدون استبدال اختيار عدد من الأفراد من العينة حسب ما يشير إليه حجم العينة المطلوب بحيث لا يمكن اختيار كل فرد مرة أخرى بمجرد اختياره. ولذلك، يتم حذف كل عنصر محدد ولا يتم استبداله.
عندما نتحدث عن أخذ العينات العشوائية البسيطة، فإننا نشير عادة إلى تلك التي لا يتم فيها استبدال الأفراد لأنها الأكثر استخدامًا في الممارسة العملية.
لتحديد احتمالية الحصول على عينة بترتيب معين في العينة العشوائية البسيطة مع الاستبدال، يتم استخدام الصيغة التالية:
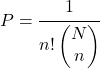
يكون
![]()
العدد الإجمالي للعناصر في السكان و
![]()
عدد عمليات الاستخراج التابعة لأداء.
ومن ناحية أخرى، إذا لم يؤخذ أمر الاستخراج بعين الاعتبار، فإن احتمال الحصول على العينة يساوي:
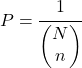
وأخيرا، يتم حساب احتمال إدراج عنصر في العينة العشوائية البسيطة دون استبدال من خلال تطبيق قاعدة لابلاس:
![]()
مزايا وعيوب أخذ العينات العشوائية البسيطة
ولأخذ العينات العشوائية البسيطة المزايا والعيوب التالية:
| ميزة | سلبيات |
|---|---|
| سهل الفهم. | من الضروري وجود قائمة بجميع عناصر السكان. |
| جميع العينات الممكنة قابلة للتجهيز. | يمكن أن يكون هذا مكلفًا للغاية مع أحجام العينات الكبيرة. |
| وعادة ما يتم الحصول على عينات تمثيلية. | يميل إلى أن يكون لديه أخطاء أكبر في أخذ العينات. |
| ليست هناك حاجة إلى معرفة تقنية للقيام بأخذ العينات. | لا يتم استغلال المعرفة التي قد تكون لدى الباحث في مجال الدراسة. |
| يسمح لك بحساب المتوسطات والانحرافات بسرعة. | قد لا تكون العينة ممثلة إذا كانت صغيرة جدًا. |
| هناك برامج إحصائية لتحليل البيانات. | غير مناسب للدراسات التي تتطلب مقابلات فردية. |
وكما رأينا، فإن إحدى الخصائص الرئيسية لأخذ العينات العشوائية البسيطة هي سهولة فهمها وتفسيرها. وفي الواقع فإن الشخص الذي يقوم بأخذ العينات لا يحتاج إلى أن يكون خبيراً في مجال التحليل. ومع ذلك، فإن هذا يمثل نقطة قوة وضعف في نفس الوقت، لأنه في الأنواع الأخرى من أخذ العينات، يمكن الاستفادة من معرفة المحلل لتحقيق أخذ عينات أفضل.
وبالمثل، بما أن أخذ العينات عشوائي، فإن احتمالات أخذ هذا العنصر أو ذاك لتكوين العينة المدروسة تكون متساوية الاحتمال، على عكس أنواع أخذ العينات الأخرى.
على الرغم من أنه يتم عادة الحصول على عينات تمثيلية من السكان، إلا أن خطأ أخذ العينات في أخذ العينات العشوائية البسيطة يكون كبيرًا مقارنة بأنواع العينات الأخرى. بالإضافة إلى ذلك، قد لا تكون العينة ممثلة حتى إذا كان حجم الأفراد صغيرًا.
من الخصائص الجذابة للغاية لأخذ العينات العشوائية البسيطة أنه يمكن تنفيذها باستخدام برامج الكمبيوتر، مما يسمح بإجراء الحسابات الإحصائية بسرعة.
وأخيرا، تجدر الإشارة إلى أن أخذ العينات العشوائية البسيطة يمكن أن يكون أكثر تكلفة من الأنواع الأخرى من أخذ العينات، وخاصة في المجموعات السكانية المتناثرة على نطاق واسع، لأنه قد يتطلب استخدام المزيد من الموارد للبحث. على سبيل المثال، نظرًا لأنها عينة عشوائية، فإن الأشخاص الذين تم اختيارهم لإجراء الدراسة قد يكونون منتشرين جغرافيًا على نطاق واسع، وبالتالي، فإن إجراء المقابلات وجهًا لوجه سيكون أكثر تكلفة بكثير.