كيفية إجراء اختبار t من عينتين في برنامج excel
يتم استخدام اختبار t المكون من عينتين لاختبار ما إذا كانت متوسطات مجتمعين متساويتين أم لا.
يشرح هذا البرنامج التعليمي كيفية إجراء اختبار t المكون من عينتين في برنامج Excel.
كيفية إجراء اختبار t من عينتين في برنامج Excel
لنفترض أن الباحثين يريدون معرفة ما إذا كان هناك نوعان مختلفان من النباتات في بلد معين لهما نفس متوسط الارتفاع. ونظرًا لأن قياس كل نبات سيستغرق وقتًا طويلاً، فقد قرروا أخذ عينة من 20 نباتًا من كل نوع.
الصورة التالية توضح الارتفاع (بالبوصة) لكل نبات في كل عينة:
يمكننا إجراء اختبار t مكون من عينتين لتحديد ما إذا كان النوعان لهما نفس متوسط الارتفاع باتباع الخطوات التالية:
الخطوة 1: تحديد ما إذا كانت فروق السكان متساوية .
عندما نقوم بإجراء اختبار t لعينتين، يجب علينا أولاً أن نقرر ما إذا كنا سنفترض أن المجتمعين لهما تباينات متساوية أو غير متساوية. بشكل عام، يمكننا أن نفترض أن المجموعات السكانية لها تباينات متساوية إذا كانت نسبة أكبر تباين في العينة إلى أصغر تباين في العينة أقل من 4:1.
يمكننا إيجاد التباين لكل عينة باستخدام دالة Excel =VAR.S(Cell range) كما هو موضح في الصورة التالية:
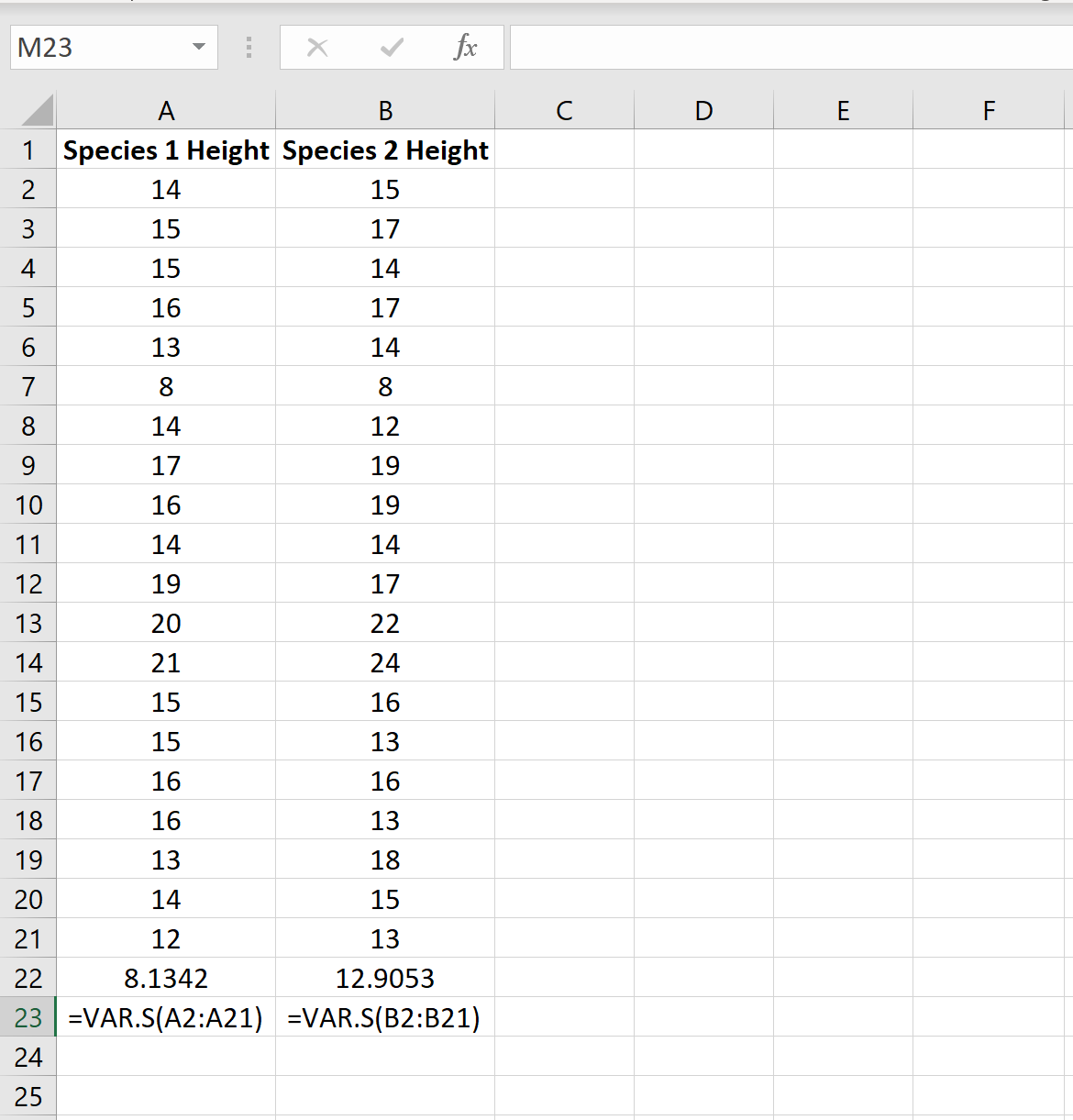
نسبة أكبر تباين في العينة إلى أصغر تباين في العينة هي 12.9053/8.1342 = 1.586 ، وهي أقل من 4. وهذا يعني أنه يمكننا افتراض أن تباينات السكان متساوية.
الخطوة 2: افتح حزمة أدوات التحليل .
في علامة التبويب “البيانات” بالشريط العلوي، انقر فوق “تحليل البيانات”.
إذا لم تجد هذا الخيار للنقر عليه، فستحتاج أولاً إلى تنزيل Analysis ToolPak ، وهو مجاني تمامًا.
الخطوة 3: حدد الاختبار المناسب للاستخدام.
حدد الخيار الذي يقول اختبار t: عينتان تفترضان تباينات متساوية ، ثم انقر فوق موافق.
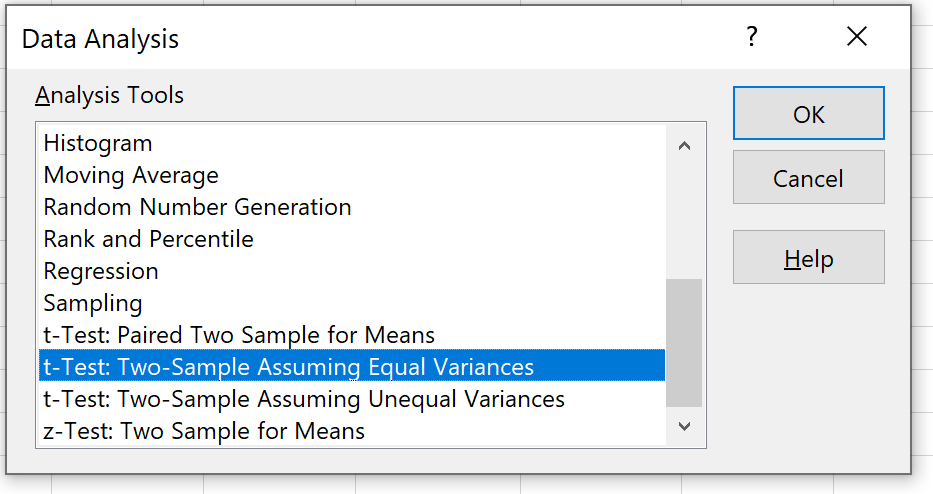
الخطوة 4: أدخل المعلومات اللازمة .
أدخل نطاق القيم للمتغير 1 (عينتنا الأولى)، المتغير 2 (عينتنا الثانية)، فرق المتوسط الافتراضي (في هذه الحالة نضع “0” لأننا نريد معرفة ما إذا كان فرق متوسط السكان الحقيقي هو 0) ، ونطاق الإخراج الذي نود أن نرى نتائج اختبار t معروضة فيه. ثم انقر فوق موافق.
الخطوة 5: تفسير النتائج .
بمجرد النقر فوق “موافق” في الخطوة السابقة، سيتم عرض نتائج اختبار t.
وإليك كيفية تفسير النتائج:
المتوسط: هذا هو متوسط كل عينة. العينة 1 يبلغ متوسط ارتفاعها 15.15 والعينة 2 يبلغ متوسط ارتفاعها 15.8 .
التباين: هذا هو التباين لكل عينة. العينة 1 بها تباين قدره 8.13 والعينة 2 بها تباين قدره 12.90 .
الملاحظات: هذا هو عدد الملاحظات في كل عينة. تحتوي كلتا العينتين على 20 ملاحظة (على سبيل المثال، 20 نباتًا فرديًا في كل عينة).
التباين المجمع: الرقم المحسوب عن طريق “تجميع” تباينات كل عينة باستخدام الصيغة s 2 p = [ (n 1 -1)s 2 1 + (n 2 -1)s 2 2 ] / (n 1 +n 2 – 2) والذي تبين أنه 10.51974 . ثم يتم استخدام هذا الرقم عند حساب إحصائيات اختبار t .
فرق المتوسط الافتراضي: الرقم الذي “نفترضه” هو الفرق بين متوسطي مجموعتي السكان. في هذه الحالة، اخترنا 0 لأننا نريد اختبار ما إذا كان الفرق بين متوسطي المجموعتين يساوي 0 أم لا، على سبيل المثال إذا لم يكن هناك فرق.
df: درجات الحرية لاختبار t، محسوبة على النحو n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: إحصائية الاختبار t , محسوبة كـ t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
في هذه الحالة، t = [15.15-15.8] / √ [10.51974(1/20+1/20)] = -0.63374 .
ثنائي الذيل P(T<=t): القيمة p لاختبار t ثنائي الذيل. في هذه الحالة، ع = 0.530047 . وهذا أكبر بكثير من alpha = 0.05، لذا فشلنا في رفض فرضية العدم. ليس لدينا ما يكفي من الأدلة لنقول أن وسائل السكان مختلفة.
t حرجة ثنائية الطرف: هذه هي القيمة الحرجة للاختبار، ويتم العثور عليها من خلال تحديد القيمة في جدول توزيع t الذي يتوافق مع اختبار ثنائي الطرف مع alpha = 0.05 وdf = 38. وتبين أن هذه هي 2، 024394 . وبما أن إحصائية اختبار t لدينا أقل من هذه القيمة، فإننا نفشل في رفض فرضية العدم. ليس لدينا ما يكفي من الأدلة لنقول أن وسائل السكان مختلفة.
لاحظ أن نهج القيمة p والقيمة الحرجة سيؤديان إلى نفس النتيجة.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إجراء أنواع أخرى من اختبارات t في Excel:
كيفية إجراء اختبار t لعينة واحدة في Excel
كيفية إجراء اختبار t للعينات المقترنة في Excel
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر