كيفية إنشاء فاصل الثقة باستخدام توزيع f

لتحديد ما إذا كانت تباينات مجتمعين متساويين، يمكننا حساب نسبة التباين σ ² ₁ / σ ² ₂ ، حيث σ ² ₁ هو تباين المجتمع 1 و σ ² ₂ هو تباين المجتمع 2.

لتقدير نسبة التباين السكاني الحقيقية، نأخذ بشكل عام عينة عشوائية بسيطة من كل مجتمع ونحسب نسبة تباين العينة، s ₁ ² / s ₂ ² ، حيث s ₁ ² و s ₂ ² هما تباينات العينة للعينة 1 والعينة . 2 على التوالي.

يفترض هذا الاختبار أن s ₁ ² و s ₂ ² تم حسابهما من عينات مستقلة بالحجم n ₁ و n ₂ ، وكلاهما من مجموعات سكانية موزعة بشكل طبيعي.

وكلما ابتعدت هذه النسبة عن الواحد، كلما كان الدليل على وجود تباينات غير متكافئة بين السكان أقوى.

يتم تعريف فاصل الثقة 100% (1-α) لـ σ ² ₁ / σ ² ₂ على النحو التالي:

(ق ₁ ² / ث ₂ ² ) * ف _{ن 1 -1, ن 2 -1, α/2} ≥ σ ² ₁ / σ ² ₂ ≥ (ق ₁ ² / ث ₂ ² ) * ف _{ن 2 -1, ن 1 -1، α/2}

حيث F _{n 2 -1، n 1 -1، α/2} و F _{n 1 -1، n 2 -1، α/2}   هي القيم الحرجة للتوزيع F لمستوى الأهمية α المختار.

توضح الأمثلة التالية كيفية إنشاء فاصل ثقة لـ σ ² ₁ / σ ² ₂ باستخدام ثلاث طرق مختلفة:

• بالأيدي
• استخدم مايكروسوفت اكسل
• استخدام البرنامج الإحصائي R

لكل من الأمثلة التالية، سوف نستخدم المعلومات التالية:

• α = 0.05
• ن ₁ = 16
• _ن2 = 11
• ق ₁ ² =28.2
• ق ₂ ² = 19.3

إنشاء فاصل ثقة يدويًا

لحساب فاصل الثقة يدويًا لـ σ ² ₁ / σ ² ₂ , سنقوم ببساطة بالتعويض عن الأرقام التي لدينا في صيغة فاصل الثقة:

(ق ₁ ² / ث ₂ ² ) * F _{n1-1, n2-1,α/2} ≥ σ ² ₁ / σ ² ₂ ≥ (ق ₁ ² / ث ₂ ² ) * F _{n2-1, n1-1, ألفا/2}

الأرقام الوحيدة التي نفتقدها هي القيم الحرجة. ولحسن الحظ، يمكننا تحديد هذه القيم الحرجة في جدول التوزيع F :

F _{n2-1، n1-1، α/2} = F _{10، 15، 0.025} = 3.0602

F _{n1-1، n2-1، α/2} = 1/ F _{15، 10، 0.025} = 1 / 3.5217 = 0.2839

(انقر لتكبير الجدول)

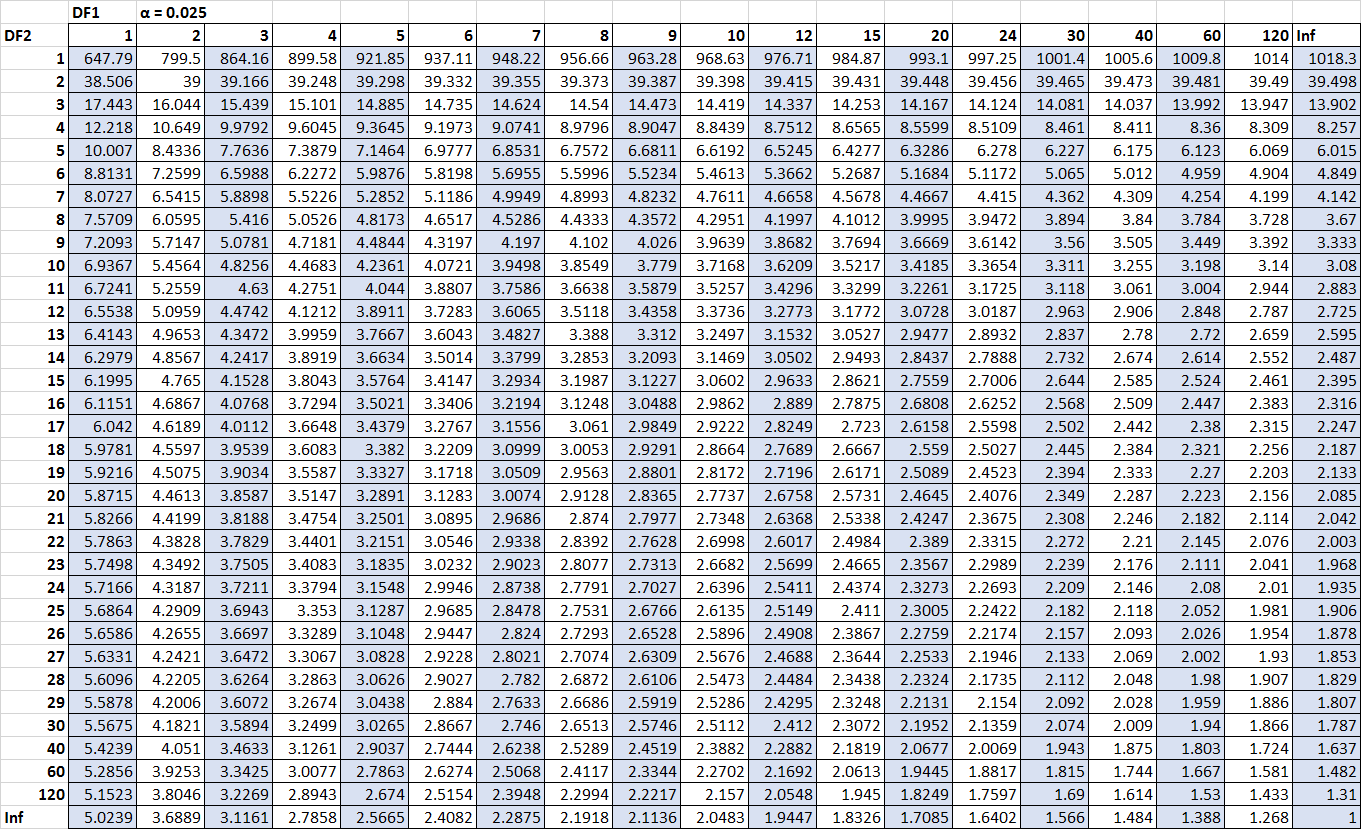
يمكننا الآن إدخال جميع الأرقام في فترة صيغة الثقة:

(ق ₁ ² / ث ₂ ² ) * F _{n1-1, n2-1,α/2} ≥ σ ² ₁ / σ ² ₂ ≥ (ق ₁ ² / ث ₂ ² ) * F _{n2-1, n1-1, ألفا/2}

(28.2 / 19.3) * (0.2839) ≥ σ ² ₁ / σ ² ₂ ≥ (28.2 / 19.3) * (3.0602)

0.4148 ≥ σ ² ₁ / σ ² ₂ ≥ 4.4714

وبالتالي فإن فاصل الثقة 95% لنسبة تباينات السكان هو (0.4148، 4.4714) .

إنشاء فاصل الثقة باستخدام Excel

توضح الصورة التالية كيفية حساب فاصل ثقة 95% لنسبة تباين المحتوى في Excel. يتم عرض الحدود الدنيا والعليا لفاصل الثقة في العمود E وتظهر الصيغة المستخدمة للعثور على الحدود الدنيا والعليا في العمود F:

وبالتالي فإن فاصل الثقة 95% لنسبة تباينات السكان هو (0.4148، 4.4714) . وهذا يطابق ما حصلنا عليه عندما قمنا بحساب فترة الثقة يدويًا.

إنشاء فاصل الثقة باستخدام R

يوضح الكود التالي كيفية حساب فاصل ثقة 95% لنسبة تباينات المحتوى في R:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

وبالتالي فإن فاصل الثقة 95% لنسبة تباينات السكان هو (0.4148، 4.4714) . وهذا يطابق ما حصلنا عليه عندما قمنا بحساب فترة الثقة يدويًا.

مصادر إضافية

كيفية قراءة لوحة التوزيع F
كيفية العثور على القيمة الحرجة F في إكسيل