Excel: حساب فاصل الثقة لمعامل الانحدار

في نموذج الانحدار الخطي، يخبرنا معامل الانحدار بمتوسط التغير في متغير الاستجابة المرتبط بزيادة وحدة واحدة في متغير التوقع.

يمكننا استخدام الصيغة التالية لحساب فاصل الثقة لمعامل الانحدار:

فاصل الثقة لـ β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

ذهب:

•   ب ₁ = معامل الانحدار المبين في جدول الانحدار
• t _{1-∝/2, n-2} = قيمة t الحرجة لمستوى الثقة 1-∝ مع درجات الحرية n-2 حيث n هو إجمالي عدد الملاحظات في مجموعة البيانات الخاصة بنا
• se(b ₁ ) = الخطأ المعياري لـ b ₁ الموضح في جدول الانحدار

يوضح المثال التالي كيفية حساب فاصل الثقة لمعامل الانحدار في Excel.

مثال: فاصل الثقة لمعامل الانحدار في Excel

لنفترض أننا نريد ملاءمة نموذج الانحدار الخطي البسيط باستخدام ساعات الدراسة كمتغير متوقع ودرجات الامتحان كمتغير استجابة لـ 15 طالبًا في فصل معين:

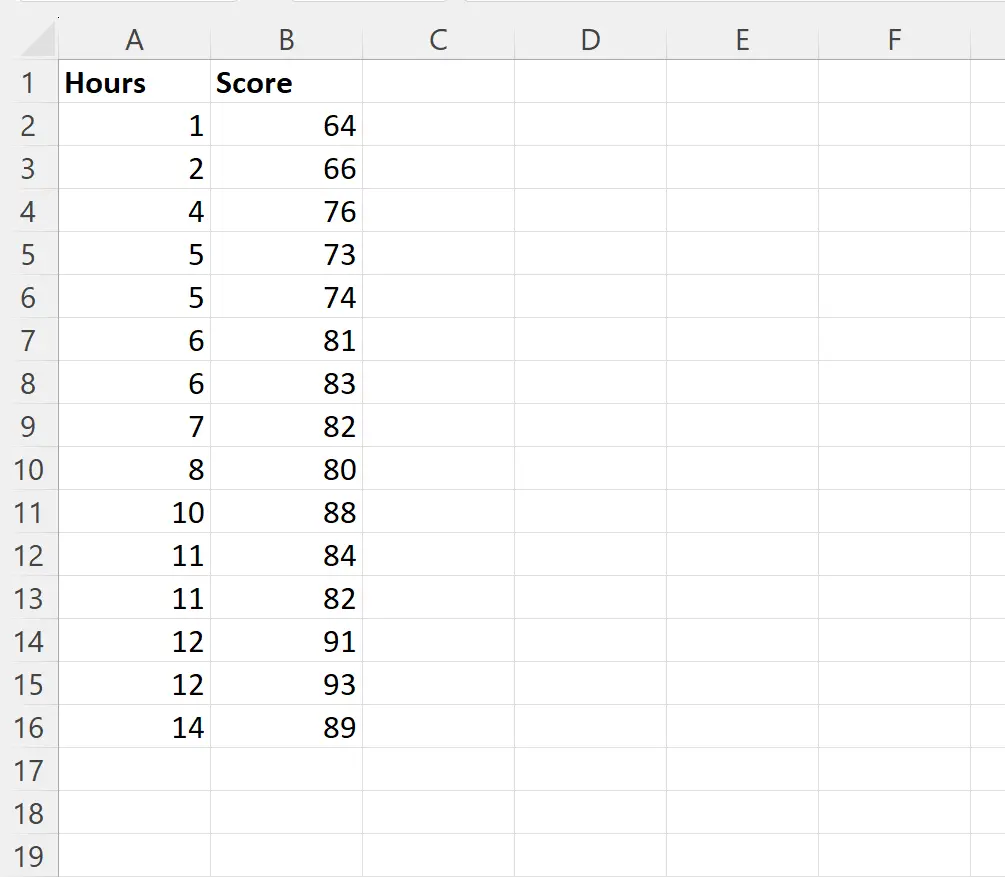
يمكننا كتابة الصيغة التالية في الخلية D2 لإجراء انحدار خطي بسيط باستخدام القيم الموجودة في عمود الساعات كمتغير التوقع والقيم الموجودة في عمود النتيجة كمتغير الاستجابة:

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

لاحظ أن الوسيطة TRUE الأولى تطلب من Excel حساب تقاطع معادلة الانحدار بشكل طبيعي دون فرضها على الصفر.

تخبر الوسيطة TRUE الثانية برنامج Excel بإنتاج إحصائيات انحدار إضافية بالإضافة إلى المعاملات.

توضح لقطة الشاشة التالية نتيجة هذه الصيغة (نوضح ما تمثله كل قيمة مخرجات في النص الأحمر الموجود أسفل الناتج):

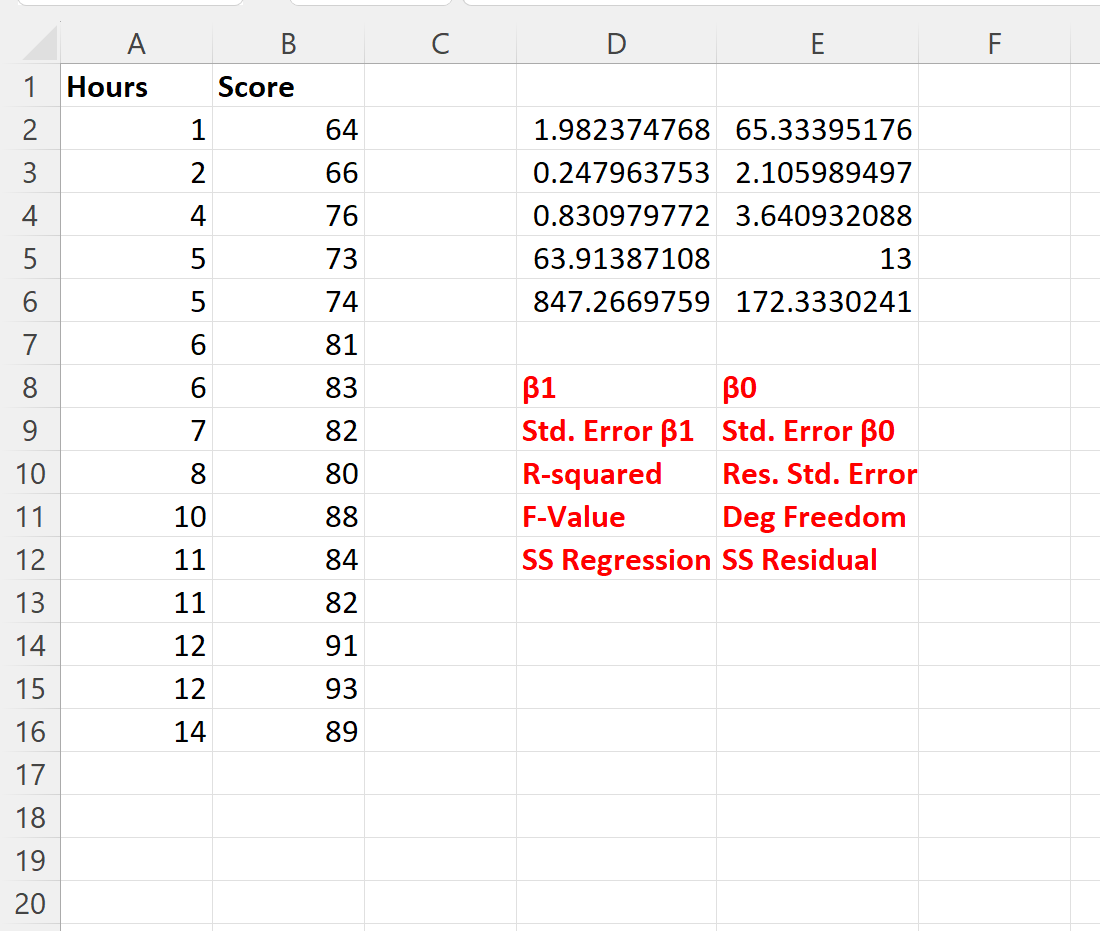
باستخدام معاملات الانحدار يمكننا كتابة معادلة الانحدار المجهزة على النحو التالي:

النتيجة = 65.334 + 1.982*(ساعات الدراسة)

لاحظ أن معامل الانحدار للساعات هو 1.982 .

يخبرنا هذا أن كل ساعة إضافية تقضيها في الدراسة ترتبط بمتوسط زيادة قدرها 1,982 في درجة الامتحان.

لحساب فاصل ثقة 95% لمعامل الانحدار، يمكننا إدخال الصيغ التالية في الخلايا H2 وH3:

• H2: = D2 – T.INV.2T(0.05, E5)*D3
• H3: = D2 + T.INV.2T(0.05, E5)*D3

توضح لقطة الشاشة التالية كيفية استخدام هذه الصيغ عمليًا:

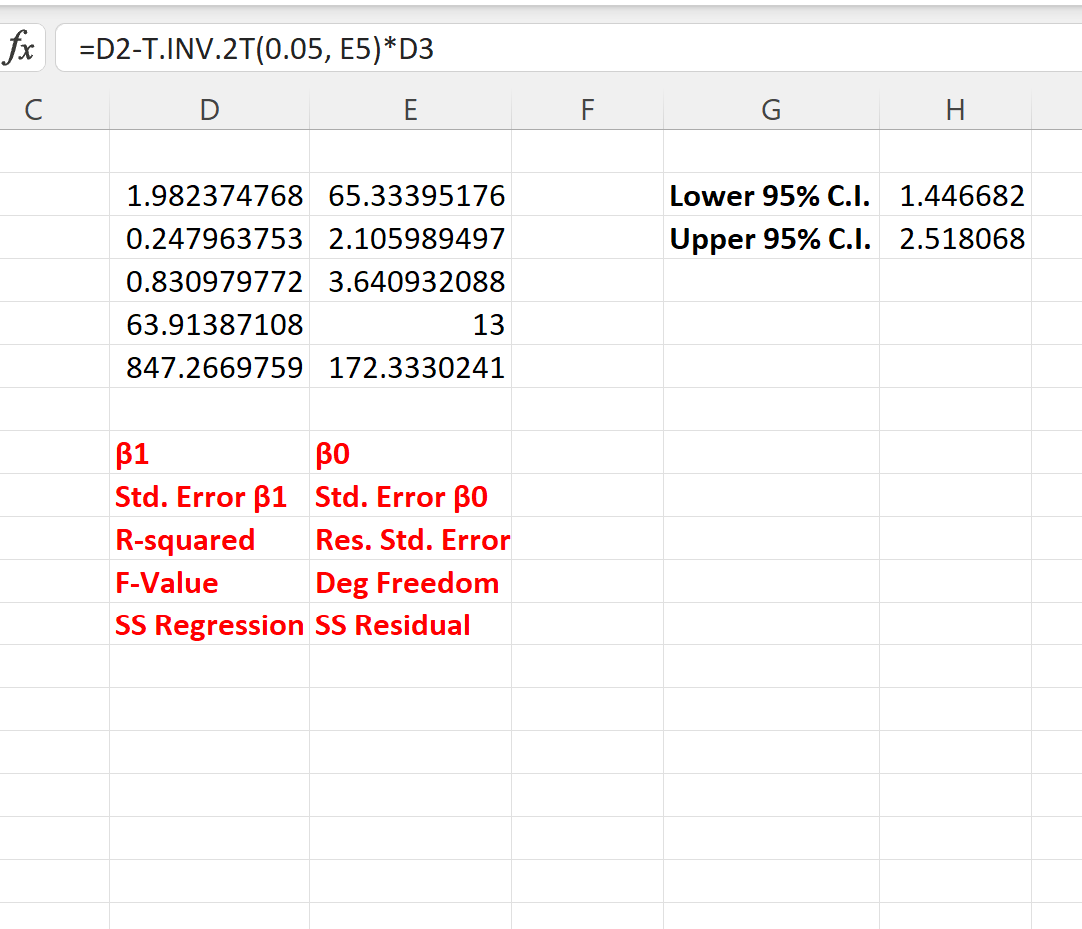
فترة الثقة 95% لمعامل الانحدار هي [1.446, 2.518] .

وبما أن فترة الثقة هذه لا تحتوي على القيمة 0 ، فيمكننا أن نستنتج أن هناك علاقة ذات دلالة إحصائية بين ساعات الدراسة ودرجة الامتحان.

يمكننا أيضًا التأكد من صحة ذلك عن طريق الحساب اليدوي لفاصل الثقة 95% لمعامل الانحدار:

• 95% CI لـ β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• 95% CI لـ β ₁ : 1.982 ± t _{0.975، 15-2} *0.248
• 95% CI لـ β ₁ : 1.982 ± 2.1604*0.248
• 95% CI لـ β ₁ : [1.446، 2.518]

فترة الثقة 95% لمعامل الانحدار هي [1.446, 2.518] .

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في Excel:

كيفية تنفيذ الانحدار الخطي البسيط في إكسيل
كيفية إجراء الانحدار الخطي المتعدد في إكسيل
كيفية تفسير القيم P في مخرجات الانحدار في Excel