فاصل الثقة للفرق في الوسائل
تشرح هذه المقالة ما هو فاصل الثقة للفرق في المتوسطات في الإحصائيات وما يتم استخدامه من أجله. لذلك، سوف تكتشف كيفية حساب فترة الثقة للفرق بين وسطين وتم حل التمرين خطوة بخطوة.
ما هو فاصل الثقة للفرق في الوسائل؟
فاصل الثقة لاختلاف المتوسطات هو فاصل يوفر قيمة قصوى وقيمة دنيا تقع بينهما قيمة الفرق بين مجموعتين من السكان عند مستوى معين من الثقة.
على سبيل المثال، إذا كان فاصل الثقة للفرق بين متوسطي مجموعتين من السكان بمستوى ثقة 95% هو (3.5)، فهذا يعني أن الفرق بين متوسطي المجموعتين سيكون بين 3 و5 مع احتمال 95 %.
لذلك، في الإحصاء، يتم استخدام فاصل الثقة للفرق في المتوسطات لتقدير قيمتين يقع بينهما الفرق بين وسطين سكانيين. وبالتالي، باستخدام بيانات من عينتين، فمن الممكن تقريب الفرق بين متوسط السكان.
صيغة فاصل الثقة للاختلاف في الوسائل
تعتمد صيغة فترة الثقة للفرق في المتوسطات على ما إذا كانت تباينات السكان معروفة أم لا، وإذا لم تكن معروفة، ما إذا كان من الممكن افتراض أن تباينات السكان متساوية أم لا. . وسنرى بعد ذلك كيف يتم حساب فترة الثقة للفرق في المتوسطات في كل حالة.
الانحرافات المعروفة
إن صيغة حساب فاصل الثقة للفرق في الوسائل عندما تكون تباينات المجموعتين معروفة بمستوى ثقة 1-α هي كما يلي:
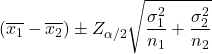
ذهب:
-

هو متوسط العينة i.
-

هو الانحراف المعياري للسكان أنا.
-

هي قيمة التوزيع الطبيعي القياسي مع الاحتمال α/2.
-

هو حجم العينة أنا.
هذه الحالة هي الأقل شيوعًا، نظرًا لأن قيمة تباينات السكان غير معروفة بشكل عام.
تباينات غير معروفة ومتساوية
عندما تكون تباينات المجموعتين غير معروفة ولكن يمكن تقديرها على أنها متساوية، تكون صيغة حساب فاصل الثقة لفرق المتوسطات بمستوى ثقة 1-α كما يلي:
![]()
ذهب:
-

هو متوسط العينة i.
-

هو الانحراف المعياري المجمعة.
-

هي قيمة توزيع الطالب لـ n 1 + n 2 -2 درجات الحرية مع احتمال α/2.
-

هو حجم العينة أنا.
وبما أنه من المفترض في هذه الحالة أن تباينات السكان متكافئة، يتم استخدام الانحراف المعياري المدمج لحساب فاصل الثقة، والذي يتم حسابه بالصيغة التالية:

ذهب
![]()
هو الانحراف المعياري للعينة i.
اختلافات غير معروفة ومختلفة
عندما تكون تباينات المجموعتين غير معروفة ولا يمكن افتراض أنها متساوية، تكون صيغة حساب فاصل الثقة لفرق المتوسطات بمستوى ثقة 1-α كما يلي:
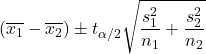
ذهب:
-

هو متوسط العينة i.
-
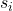
هو الانحراف المعياري للعينة i.
-

هي قيمة توزيع الطالب باحتمال α/2.
-

هو حجم العينة أنا.
في هذه الحالة يتم حساب درجات حرية توزيع الطالب باستخدام الصيغة التالية:

ذهب
![]()
هو الانحراف المعياري للعينة i.
مثال ملموس على فترة الثقة للفرق في الوسائل
بعد أن رأينا تعريف فترة الثقة للفرق بين الوسطين وما هي الصيغ المختلفة، سنرى الآن مثالًا ملموسًا للانتهاء من استيعاب كيفية حساب فترة الثقة للفرق بين وسطين.
- نريد دراسة تأثير التبغ على الوزن عند الولادة للأطفال. للقيام بذلك، يتم مقارنة عينتين: العينة الأولى تتكون من أطفال أمهاتهم غير مدخنات والعينة الثانية تتكون من أطفال أمهاتهم مدخنات (محددات العينة موضحة أدناه). احسب فترة الثقة للفرق في المتوسطات بمستوى ثقة 95%.
- الأمهات غير المدخنات:
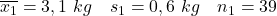
- الأمهات المدخنات:
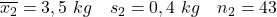
- الأمهات غير المدخنات:
في هذه الحالة لا نعرف قيم التباينات السكانية، ولكن يمكننا أن نفترض أن التباينات السكانية متكافئة لأننا نتعامل مع مجتمعين لهما خصائص متشابهة جدًا. ولذلك فإن صيغة فترة الثقة للفرق في الوسائل التي يجب أن نستخدمها هي:
![]()
وبذلك نحسب الانحراف المعياري المجمع عن الانحرافات المعيارية للعينتين:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
وبالمثل، يجب أن نجد قيمة توزيع t للطالب بمقدار 80 درجة حرية باحتمال 2.5% في جدول التوزيع الاحتمالي لتوزيع t للطالب :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
أخيرًا، نستبدل البيانات في صيغة فاصل الثقة للفرق في المتوسطات ونجري الحسابات:
![]()
![]()
![]()
وبالتالي فإن فترة الثقة للاختلاف في وسائل المشكلة هي كما يلي:
![]()