الفرضيات الثلاث التي تمت صياغتها في اختبار t المزدوج

يتم استخدام اختبار t للعينات المقترنة لمقارنة متوسطي عينتين عندما يمكن ربط كل ملاحظة في عينة واحدة بملاحظة في العينة الأخرى.

يقدم هذا النوع من الاختبارات الافتراضات التالية حول البيانات:

1. الاستقلال: يجب أن تكون كل ملاحظة مستقلة عن أي ملاحظة أخرى.

2. الحالة الطبيعية: يجب أن تكون الاختلافات بين الأزواج موزعة بشكل طبيعي تقريبًا.

3. لا توجد قيم متطرفة: لا ينبغي أن تكون هناك قيم متطرفة في الاختلافات.

إذا لم يتم استيفاء واحد أو أكثر من هذه الافتراضات، فقد تكون نتائج اختبار t للعينات المقترنة غير موثوقة أو مضللة.

نقدم في هذا البرنامج التعليمي شرحًا لكل افتراض، وكيفية تحديد ما إذا كان الافتراض قد تحقق، وماذا تفعل إذا تم انتهاكه.

الفرضية 1: الاستقلال

يفترض اختبار t للعينات المقترنة أن كل ملاحظة مستقلة عن جميع الملاحظات الأخرى.

كيفية التحقق من هذه الفرضية

إن أبسط طريقة للتحقق من هذا الافتراض هي التحقق من أن كل ملاحظة تم جمعها باستخدام طريقة أخذ العينات العشوائية .

إذا تم استخدام طريقة أخذ العينات العشوائية (مثل أخذ العينات العشوائية البسيطة)، فيمكننا أن نفترض أن كل ملاحظة مستقلة عن جميع الملاحظات الأخرى.

ماذا تفعل إذا لم يتم احترام هذا الافتراض

إذا لم يتم استيفاء هذا الافتراض، فإن نتائج اختبار t للعينات المقترنة تكون غير صالحة تمامًا.

في هذا السيناريو، من الأفضل جمع ملاحظات جديدة باستخدام طريقة أخذ العينات العشوائية للتأكد من أن كل ملاحظة مستقلة.

الفرضية 2: الحياة الطبيعية

يفترض اختبار t للعينات المقترنة أن الاختلافات بين الأزواج يجب أن تكون موزعة بشكل طبيعي تقريبًا.

يعد هذا افتراضًا حاسمًا لأنه إذا لم يتم توزيع الاختلافات بين الأزواج بشكل طبيعي، فليس من الصحيح استخدام القيمة الاحتمالية للاختبار لاستخلاص النتائج.

كيفية التحقق من هذه الفرضية

أسهل طريقة لاختبار هذه الفرضية هي ببساطة إنشاء رسم بياني للاختلافات المقترنة والتحقق بصريًا مما إذا كان الرسم البياني له شكل جرس أم لا.

على سبيل المثال، إذا كان الرسم البياني يبدو بهذا الشكل، فسنقول أن افتراض الحالة الطبيعية قد تم استيفاءه:

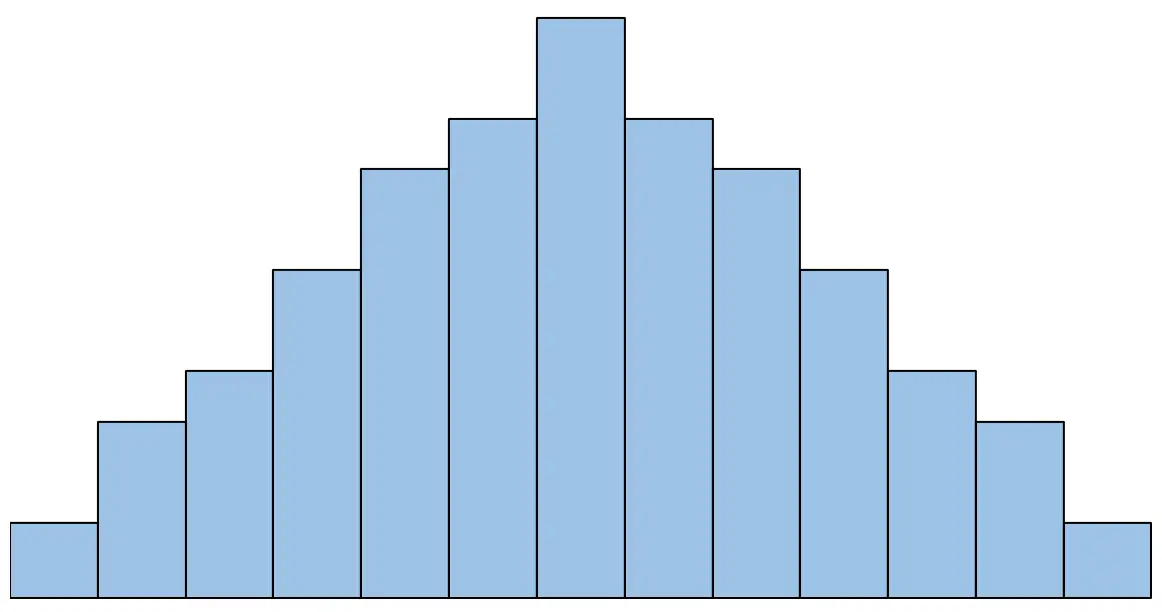
ومع ذلك، إذا كان الرسم البياني يبدو هكذا، فسنقول أن افتراض الحالة الطبيعية لم يتم استيفاءه:

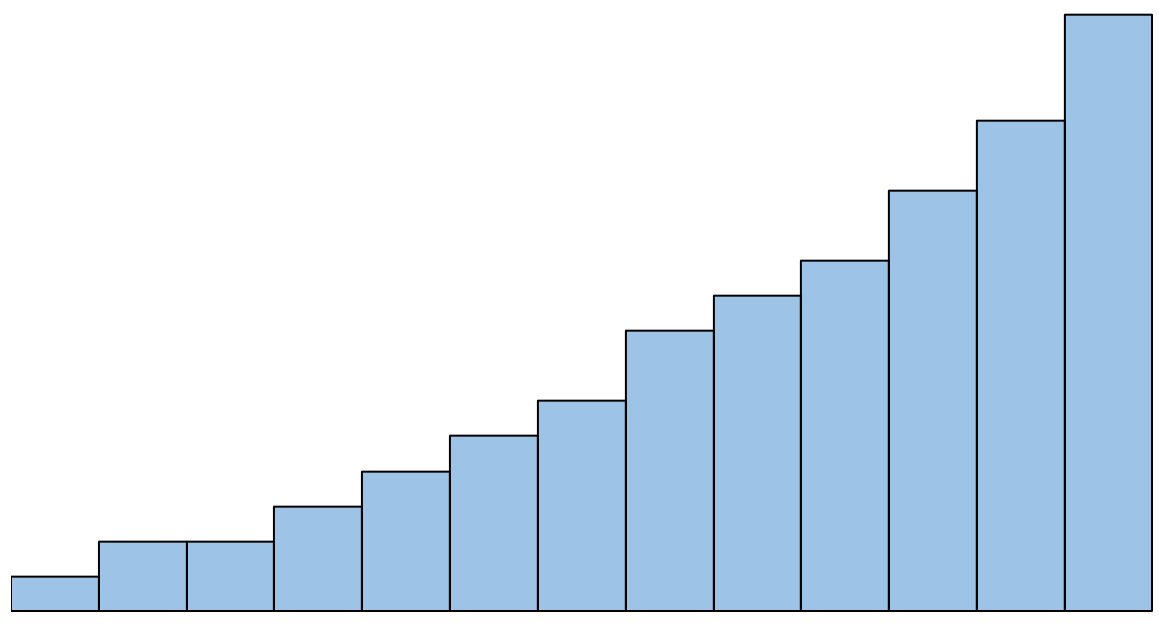
ماذا تفعل إذا لم يتم احترام هذا الافتراض

إذا تم انتهاك هذا الافتراض، فيمكننا إجراء اختبار رتبة موقعة ويلكوكسون ، والذي يعتبر المعادل غير المعلمي لاختبار t للعينات المقترنة ولا يفترض أن الاختلافات المقترنة موزعة بشكل طبيعي.

الفرضية 3: لا توجد قيم متطرفة

يفترض اختبار t للعينات المقترنة عدم وجود قيم متطرفة في البيانات.

كيفية التحقق من هذه الفرضية

أسهل طريقة لاختبار هذه الفرضية هي إنشاء مخطط مربع للاختلافات المقترنة والتحقق بصريًا من وجود أي قيم متطرفة.

على سبيل المثال، لنفترض أن المخطط المربع للاختلافات المقترنة يبدو كما يلي:

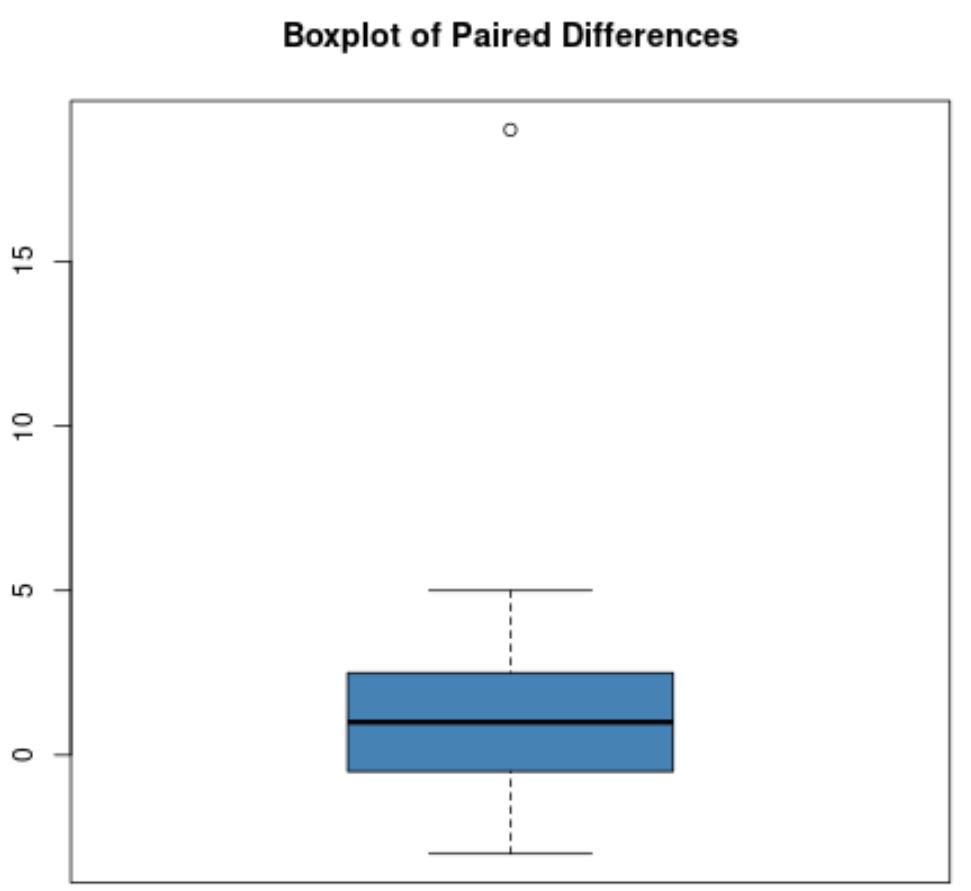
معظم الفروق الزوجية قريبة من الصفر، ولكن هناك فرق زوجي واحد يساوي حوالي 19، وهو ما يعد قيمة متطرفة بشكل واضح.

ملاحظة : تُستخدم الدائرة عادةً في مخطط مربع للإشارة إلى قيمة متطرفة.

ومع ذلك، لنفترض أن المخطط المربع للاختلافات المقترنة يبدو كما يلي:

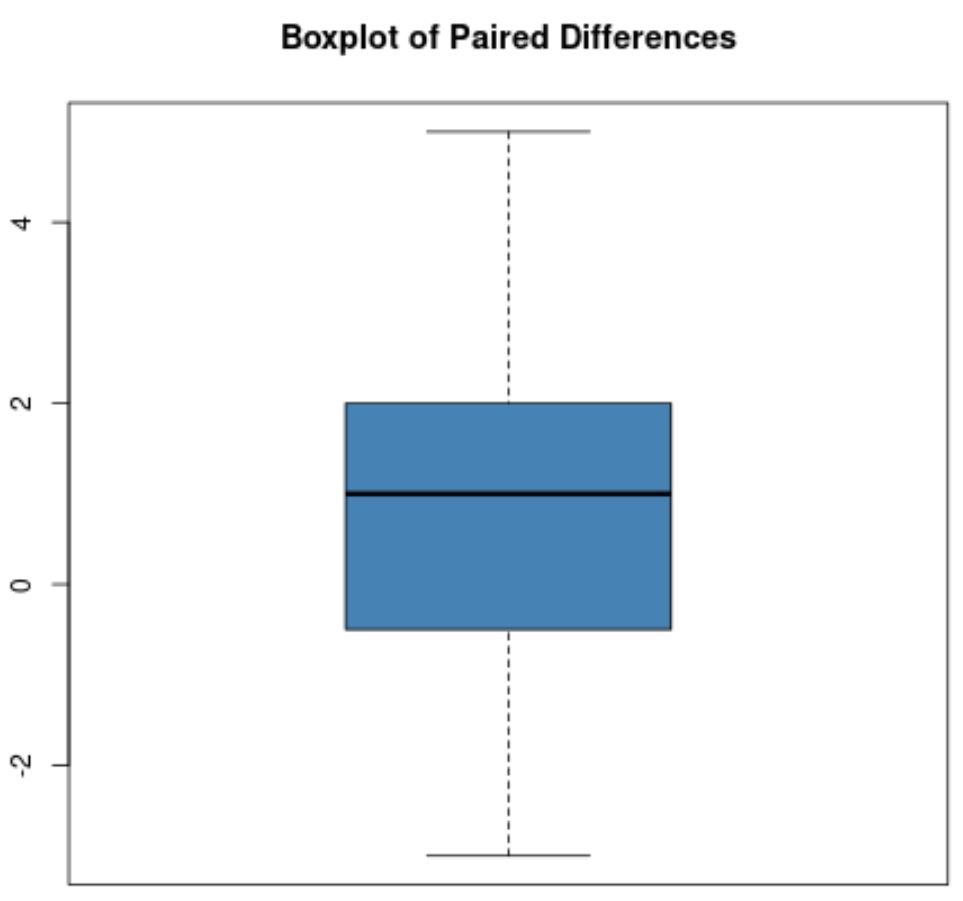
لا توجد قيم متطرفة واضحة في هذا الصندوق، لذلك سنفترض أنه لا توجد قيم متطرفة في البيانات.

ماذا تفعل إذا لم يتم احترام هذا الافتراض

إذا تم انتهاك هذا الافتراض، فقد تتأثر نتائج اختبار t للعينات المقترنة بشكل غير طبيعي بالقيمة المتطرفة.

في هذا السيناريو، يمكنك إزالة القيمة المتطرفة إذا كنت تعتقد أنها تمثل نقطة بيانات خاطئة أو أنها نتيجة لخطأ في إدخال البيانات.

وبدلاً من ذلك، يمكنك الاحتفاظ بالقيمة المتطرفة وملاحظةها ببساطة عند الإبلاغ عن نتائج اختبار t للعينات المقترنة.

مصادر إضافية

تشرح البرامج التعليمية التالية الافتراضات التي تم إجراؤها في الاختبارات الإحصائية الأخرى:

الفرضيات الأربع التي تمت صياغتها في اختبار t
الفرضيات الأربع لاختبار مربع كاي
الفرضيات الأربع للاختبارات البارامترية