الاختلاف داخل المجموعة أو بين المجموعة في anova
يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كانت وسائل ثلاث مجموعات مستقلة أو أكثر متساوية أم لا.
يستخدم تحليل التباين الأحاديالفرضيات الصفرية والبديلة التالية:
- H 0 : جميع وسائل المجموعة متساوية.
- HA : يختلف متوسط مجموعة واحدة على الأقل عن المجموعات الأخرى.
في كل مرة تقوم فيها بإجراء تحليل التباين أحادي الاتجاه، سينتهي بك الأمر بجدول ملخص يبدو كما يلي:
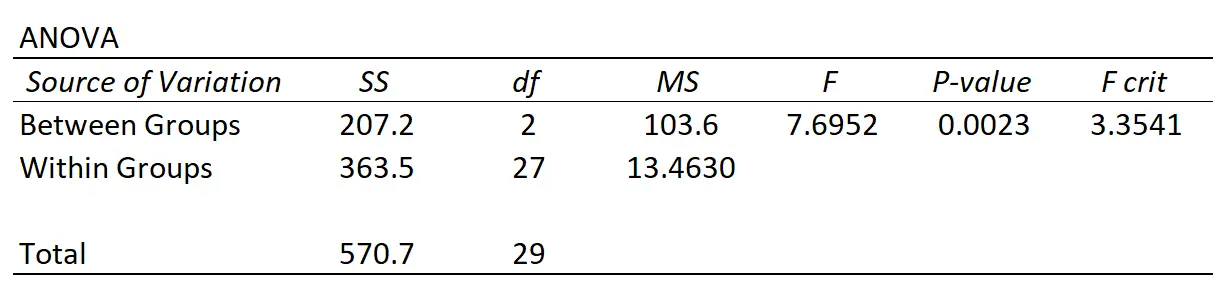
يمكننا أن نرى أن هناك مصدرين مختلفين للتباين يقيسهما تحليل التباين (ANOVA):
التباين بين المجموعات : التباين الكلي بين متوسط كل مجموعة والمعدل العام.
التباين داخل المجموعة : التباين الإجمالي للقيم الفردية في كل مجموعة ومتوسط مجموعتها.
إذا كان التباين بين المجموعات مرتفعًا بالنسبة للتباين داخل المجموعة، فستكون إحصائيات F الخاصة بـ ANOVA أعلى وستكون القيمة p المقابلة أقل، مما يزيد من احتمالية رفض الفرضية الصفرية التي بموجبها يتم رفض الفرضية الصفرية. وسائل المجموعة متساوية.
يوضح المثال التالي كيفية حساب التباين بين المجموعة والتباين داخل المجموعة لتحليل التباين أحادي الاتجاه عمليًا.
مثال: حساب التباين داخل المجموعة وبين المجموعات في ANOVA
لنفترض أننا نريد تحديد ما إذا كانت ثلاث طرق دراسة مختلفة تؤدي إلى متوسط درجات مختلفة في الامتحان. ولاختبار ذلك، قمنا بتجنيد 30 طالبًا وتخصيص 10 منهم بشكل عشوائي لاستخدام طريقة دراسة مختلفة.
وفيما يلي نتائج امتحانات الطلاب في كل مجموعة:
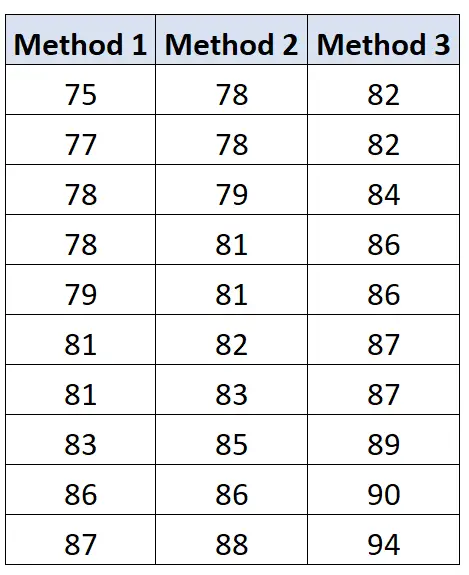
يمكننا استخدام الصيغة التالية لحساب التباين بين المجموعات :
التباين بين المجموعات = Σn j (X j – X ..) 2
ذهب:
- n j : حجم العينة للمجموعة j
- Σ : رمز يعني “المجموع”
- X j : متوسط المجموعة j
- عاشراً : المتوسط العام
ولحساب هذه القيمة سنقوم أولاً بحساب متوسط كل مجموعة والمعدل العام:
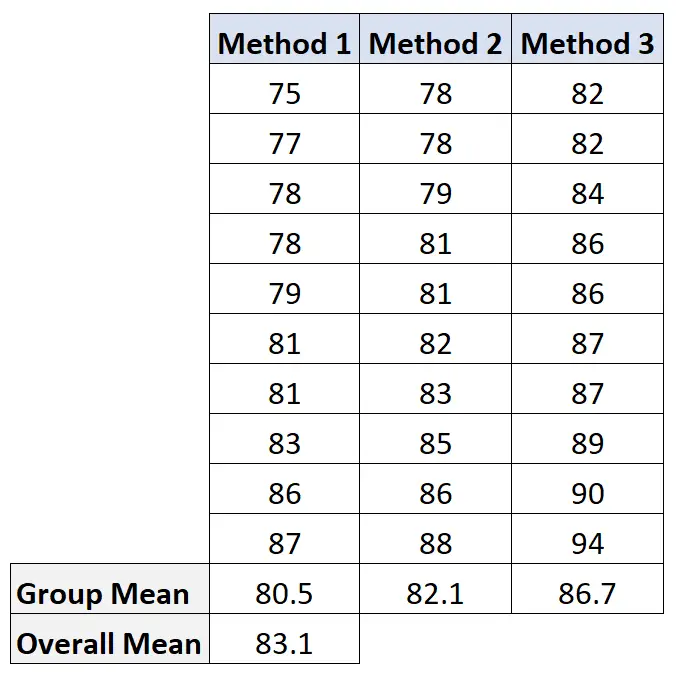
ثم نحسب التباين بين المجموعات كما يلي: 10(80.5-83.1) 2 + 10(82.1-83.1) 2 + 10(86.7-83.1) 2 = 207.2 .
ثم يمكننا استخدام الصيغة التالية لحساب التباين داخل المجموعة :
الاختلاف داخل المجموعة : Σ(X ij – X j ) 2
ذهب:
- Σ : رمز يعني “المجموع”
- X ij : الملاحظة رقم 1 للمجموعة j
- X j : متوسط المجموعة j
في مثالنا، نحسب التباين داخل المجموعة على النحو التالي:
المجموعة 1: (75-80.5) 2 + (77-80.5) 2 + (78-80.5) 2+ (78-80.5) 2+ (79-80.5) 2+ (81-80.5) 2+ (81-80.5) 2+ (83-80.5) 2+ (86-80.5) 2+ (87-80.5) 2 = 136.5
المجموعة 2: (78-82.1) 2 + (78-82.1) 2 + (79-82.1) 2+ (81-82.1) 2+ (81-82.1) 2+ (82-82.1) 2+ (83-82.1) 2+ (85-82.1) 2+ (86-82.1) 2+ (88-82.1) 2 = 104.9
المجموعة 3: (82-86.7) 2 + (82-86.7) 2 + (84-86.7) 2+ (86-86.7) 2+ (86-86.7) 2+ (87-86.7) 2+ (87-86.7) 2+ (89-86.7) 2+ (90-86.7) 2+ (94-86.7) 2 = 122.1
التباين داخل المجموعة: 136.5 + 104.9 + 122.1 = 363.5
إذا استخدمنا برنامجًا إحصائيًا لإجراء تحليل التباين أحادي الاتجاه باستخدام مجموعة البيانات هذه، فسنحصل على جدول تحليل التباين التالي:
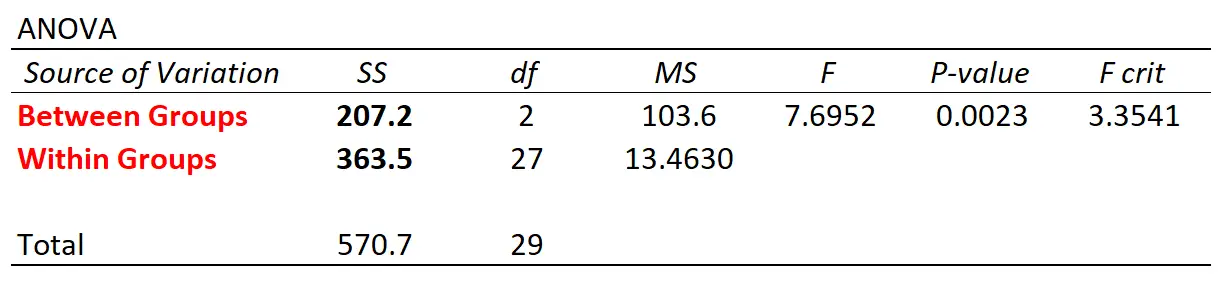
لاحظ أن قيم التباين بين المجموعة وداخل المجموعة تتطابق مع تلك التي قمنا بحسابها يدويًا.
تعد إحصائيات F الإجمالية في الجدول طريقة لقياس العلاقة بين التباين بين المجموعات والتباين داخل المجموعة.
كلما كانت إحصائية F أكبر، زاد التباين بين المجموعات بالنسبة إلى التباين داخل المجموعات.
لذلك، كلما كانت إحصائية F أكبر، كان من الواضح أن هناك فرقًا بين متوسطات المجموعة.
يمكننا أن نرى في هذا المثال أن القيمة p التي تتوافق مع إحصائيات F البالغة 7.6952 هي .0023 .
وبما أن هذه القيمة أقل من α = 0.05، فإننا نرفض الفرضية الصفرية لتحليل التباين (ANOVA) ونستنتج أن تقنيات الدراسة الثلاثة لا تؤدي إلى نفس النتيجة في الامتحان.
مصادر إضافية
توفر البرامج التعليمية التالية معلومات إضافية حول نماذج ANOVA:
مقدمة إلى تحليل التباين الأحادي (One-Way ANOVA).
كيفية تفسير قيمة F وقيمة P في ANOVA
الدليل الكامل: كيفية الإبلاغ عن نتائج ANOVA
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر