قانون الاحتمال الكلي: التعريف والأمثلة
في نظرية الاحتمالات، يعد قانون الاحتمال الإجمالي طريقة مفيدة للعثور على احتمال الحدث A عندما لا نعرف احتمال A بشكل مباشر ولكننا نعلم أن الأحداث B 1 , B 2 , B 3 … تشكل قسمًا. من فضاء العينة S .
يحدد هذا القانون ما يلي:
قانون الاحتمال الكلي
إذا كانت B 1 , B 2 , B 3 … تشكل قسماً من فضاء العينة S ، فيمكننا حساب احتمال الحدث A كما يلي:
P( A ) = ΣP( A | B i )*P( B i )
أسهل طريقة لفهم هذا القانون هي أن نأخذ مثالاً بسيطًا.
لنفترض أن هناك حقيبتين في صندوق يحتوي على الكرات التالية:
- الكيس 1: 7 كرات حمراء و3 كرات خضراء
- الكيس 2: 2 رخام أحمر و8 رخام أخضر
إذا اخترنا أحد الأكياس عشوائيًا، ثم اخترنا عشوائيًا رخامًا من ذلك الكيس، فما احتمال أن تكون رخامًا أخضر اللون؟
في هذا المثال، لنفترض أن P( G ) = احتمال اختيار رخام أخضر. إنه الاحتمال الذي يهمنا، لكننا لا نستطيع حسابه بشكل مباشر.
بدلاً من ذلك، نحتاج إلى استخدام الاحتمال الشرطي لـ G ، في ضوء بعض الأحداث B حيث يشكل B i قسمًا من مساحة العينة S. في هذا المثال، لدينا الاحتمالات الشرطية التالية:
- ف(ز| B1 ) = 3/10 = 0.3
- ف(ز| B2 ) = 8/10 = 0.8
لذا، وباستخدام قانون الاحتمال الكلي، يمكننا حساب احتمال اختيار رخام أخضر على النحو التالي:
- P(G) = ΣP(G|B i )*P(B i )
- P(G) = P(G|B 1 )*P(B 1 ) + P(G|B 2 )*P(B 2 )
- ف(ز) = (0.3)*(0.5) + (0.8)*(0.5)
- ف (ز) = 0.55
إذا اخترنا أحد الأكياس عشوائيًا، ثم اخترنا عشوائيًا رخامًا من ذلك الكيس، فإن احتمال اختيار رخام أخضر هو 0.55 .
اقرأ المثالين التاليين لترسيخ فهمك لقانون الاحتمال الكلي.
المثال 1: الحاجيات
تقوم الشركة “أ” بتوريد 80% من الأدوات إلى ورشة سيارات، وتبين أن 1% فقط من الأدوات معيبة. تقوم الشركة “ب” بتزويد ورشة إصلاح السيارات بنسبة 20% المتبقية من الأدوات المصغّرة، وتبين أن 3% من أدواتها معيبة.
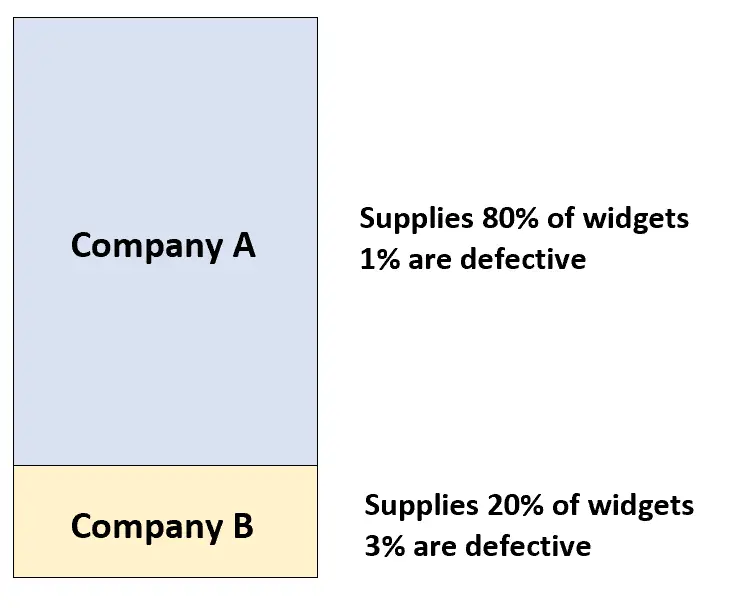
إذا قام أحد العملاء بشراء أداة بشكل عشوائي من ورشة لتصليح السيارات، ما هو احتمال أن تكون معيبة؟
إذا تركنا P( D ) = احتمال أن تكون القطعة معيبة و P(B i ) احتمال أن تأتي القطعة من إحدى الشركات، فيمكننا حساب احتمال شراء القطعة المعيبة على النحو التالي:
- P(D) = ΣP(D|B i )*P(B i )
- ف(د) = ف(د|ب 1 )*ف(ب 1 ) + ف(د|ب 2 )*ف(ب 2 )
- ف(د) = (0.01)*(0.80) + (0.03)*(0.20)
- ف (د) = 0.014
إذا اشترينا عنصر واجهة مستخدم بشكل عشوائي من متجر السيارات هذا، فإن احتمال أن يكون معيبًا هو 0.014 .
مثال 2: الغابات
تشغل الغابة أ 50% من المساحة الإجمالية لمنتزه معين، كما أن 20% من النباتات الموجودة في هذه الغابة سامة. تشغل الغابة ب 30% من المساحة الإجمالية و40% من النباتات التي تحتوي عليها سامة. تحتل الغابة C نسبة 20% المتبقية من الأراضي و70% من النباتات الموجودة هناك سامة.

إذا مشينا بشكل عشوائي في هذه الحديقة وقمنا بقطف نبات من الأرض، ما مدى احتمالية أن يكون سامًا؟
إذا تركنا P( P ) = احتمال أن يكون النبات سامًا، و P(B i ) احتمال أننا دخلنا إحدى الغابات الثلاث، فيمكننا حساب احتمال أن يكون النبات الذي تم اختياره عشوائيًا سامًا مثل:
- P(P) = ΣP(P|B i )*P(B i )
- P(P) = P(P|B 1 )*P(B 1 ) + P(P|B 2 )*P(B 2 ) + P(P|B 3 )*P(B 3 )
- ف(ف) = (0.20)*(0.50) + (0.40)*(0.30) + (0.70)*(0.20)
- ف (ف) = 0.36
إذا اخترنا نباتًا من الأرض عشوائيًا، فإن احتمال أن يكون سامًا هو 0.36 .
مصادر إضافية
توفر البرامج التعليمية التالية معلومات إضافية حول موضوعات الاحتمالية:
كيفية العثور على متوسط التوزيع الاحتمالي
كيفية العثور على الانحراف المعياري للتوزيع الاحتمالي
حاسبة التوزيع الاحتمالي