كيفية العثور على قيمة p من درجة t في excel

في كثير من الأحيان، في الإحصاء، يؤدي اختبار الفرضية إلى إحصائية اختبار T-score. بمجرد العثور على درجة t تلك، عادةً ما نجد القيمة p المرتبطة بها. إذا كانت هذه القيمة p أقل من مستوى ألفا معين (على سبيل المثال 0.10، 0.05، 0.01)، فإننا نرفض الفرضية الصفرية للاختبار ونستنتج أن نتائجنا مهمة.

يشرح هذا البرنامج التعليمي كيفية العثور على القيمة p من نتيجة t في Excel باستخدام الدالة T.DIST ، التي تأخذ الوسيطات التالية:

T.DIST (x، deg_freedom)

ذهب:

• x: درجة T التي تهمنا.
• deg_freedom: درجات الحرية.

دعونا نرى بعض الأمثلة.

مثال 1: قيمة P من t-score (ثنائي الذيل)

يريد عالم نبات معرفة ما إذا كان متوسط ارتفاع نوع معين من النباتات يساوي 15 بوصة. وفي عينة عشوائية مكونة من 12 نباتًا، وجدت أن متوسط ارتفاع العينة هو 14.33 بوصة، والانحراف المعياري للعينة هو 1.37 بوصة.

قم بإجراء اختبار فرضية ثنائي الذيل باستخدام مستوى ألفا قدره 0.05 لتحديد ما إذا كان متوسط الارتفاع يساوي 15 بوصة.

الخطوة الأولى: اذكر الفرضيات.

الفرضية الصفرية (H ₀ ): μ = 15

الفرضية البديلة : (ها): μ ≠ 15

الخطوة 2: ابحث عن درجة T ودرجات الحرية.

النتيجة t = ( x -μ) / (s/√n) = (14.33-15) / (1.37/√12) = -1.694 .

درجات الحرية = ن-1 = 12-1 = 11 .

الخطوة 3: ابحث عن القيمة الاحتمالية لدرجة t باستخدام برنامج Excel.

للعثور على القيمة الاحتمالية لدرجة t، سنستخدم الصيغة التالية في برنامج Excel:

=T.DIST.2T(ABS(-1.694)، 11)

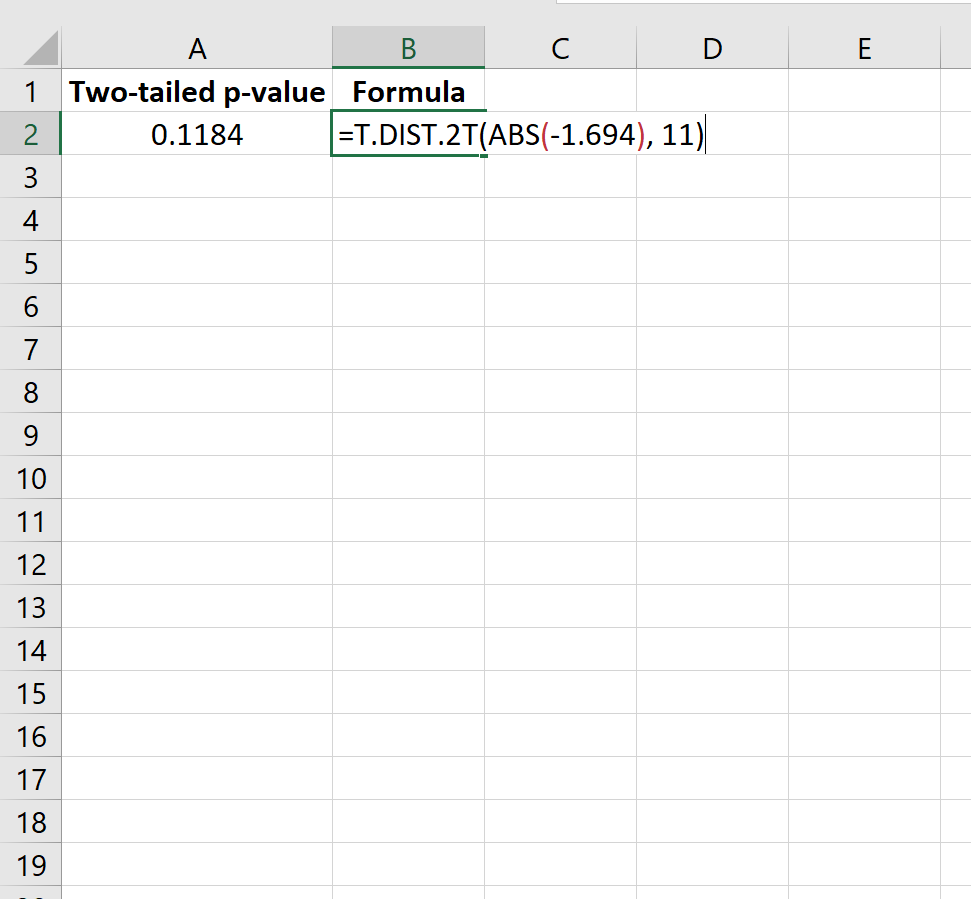
يخبرنا هذا أن القيمة p على الوجهين هي 0.1184 .

الخطوة الرابعة: رفض أو عدم رفض الفرضية الصفرية.

نظرًا لأن القيمة p البالغة 0.1184 لا تقل عن مستوى ألفا المختار وهو 0.05 ، فإننا نفشل في رفض فرضية العدم. ليس لدينا ما يكفي من الأدلة لنقول أن متوسط ارتفاع النبات يختلف عن 15 بوصة.

مثال 2: قيمة P من درجة T (أحادية الجانب)

تريد إحدى الشركات معرفة ما إذا كان النوع الجديد من البطاريات يتمتع بمتوسط عمر أطول من البطارية القياسية الحالية، والتي يبلغ متوسط عمرها 18 ساعة. وفي عينة عشوائية مكونة من 25 بطارية جديدة، وجدوا أن متوسط العمر هو 19 ساعة مع انحراف معياري قدره 4 ساعات.

قم بإجراء اختبار فرضي أحادي الجانب باستخدام مستوى ألفا قدره 0.05 لتحديد ما إذا كان متوسط عمر البطارية الجديدة أطول من متوسط عمر البطارية القياسية الحالية.

الخطوة الأولى: اذكر الفرضيات.

الفرضية الصفرية (H ₀ ): μ ≥ 18

الفرضية البديلة : (Ha): μ > 18

الخطوة 2: ابحث عن درجة T ودرجات الحرية.

النتيجة t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1.25 .

درجات الحرية = ن-1 = 25-1 = 24 .

الخطوة 3: ابحث عن القيمة الاحتمالية لدرجة t باستخدام برنامج Excel.

للعثور على القيمة الاحتمالية لدرجة t، سنستخدم الصيغة التالية في برنامج Excel:

=T.DIST.RT(1.25, 24)

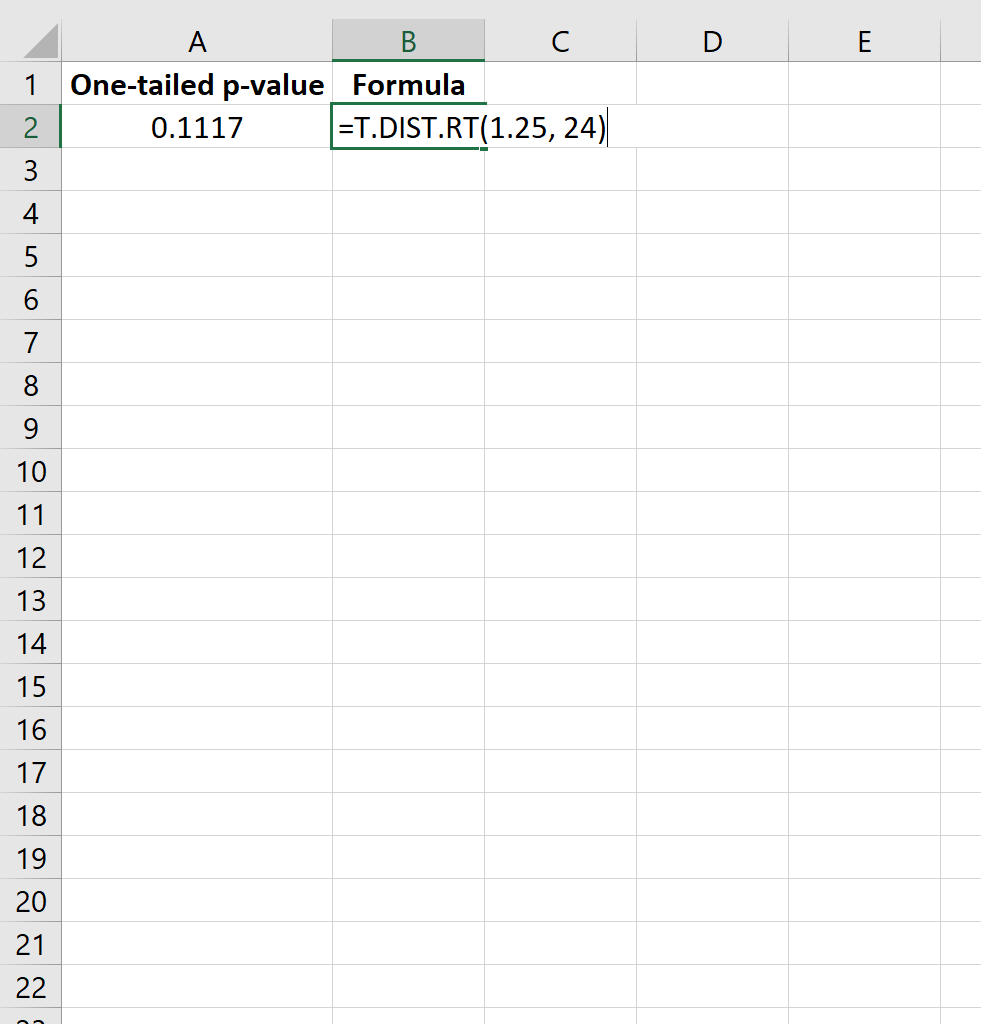
يخبرنا هذا أن القيمة p أحادية الجانب هي 0.1117 .

الخطوة الرابعة: رفض أو عدم رفض الفرضية الصفرية.

نظرًا لأن القيمة p البالغة 0.1117 أكبر من مستوى ألفا المختار وهو 0.05 ، فإننا نفشل في رفض فرضية العدم. ليس لدينا أدلة كافية للقول بأن متوسط عمر البطارية الجديدة أطول من متوسط عمر البطارية القياسية الحالية.

لمزيد من البرامج التعليمية حول الإحصائيات في Excel، تأكد من مراجعة قائمتنا الكاملة لأدلة Excel .