الفرق بين قيم t وقيم p في الإحصائيات
المصطلحان اللذان غالبًا ما يخلطهما الطلاب في الإحصاء هما قيم t وقيم p .
لفهم الفرق بين هذه المصطلحات، من المفيد فهم اختبارات t .
بشكل عام، هناك ثلاثة أنواع مختلفة من اختبارات t:
- اختبار t لعينة واحدة : يستخدم لاختبار ما إذا كان متوسط المجتمع يساوي قيمة معينة.
- اختبار t لعينتين : يستخدم لاختبار ما إذا كانت متوسطات مجموعتين من السكان متساوية.
- اختبار t للعينات المقترنة : يستخدم لاختبار ما إذا كانت متوسطات مجموعتين من السكان متساوية عندما يمكن ربط كل ملاحظة في عينة واحدة بملاحظة في العينة الأخرى.
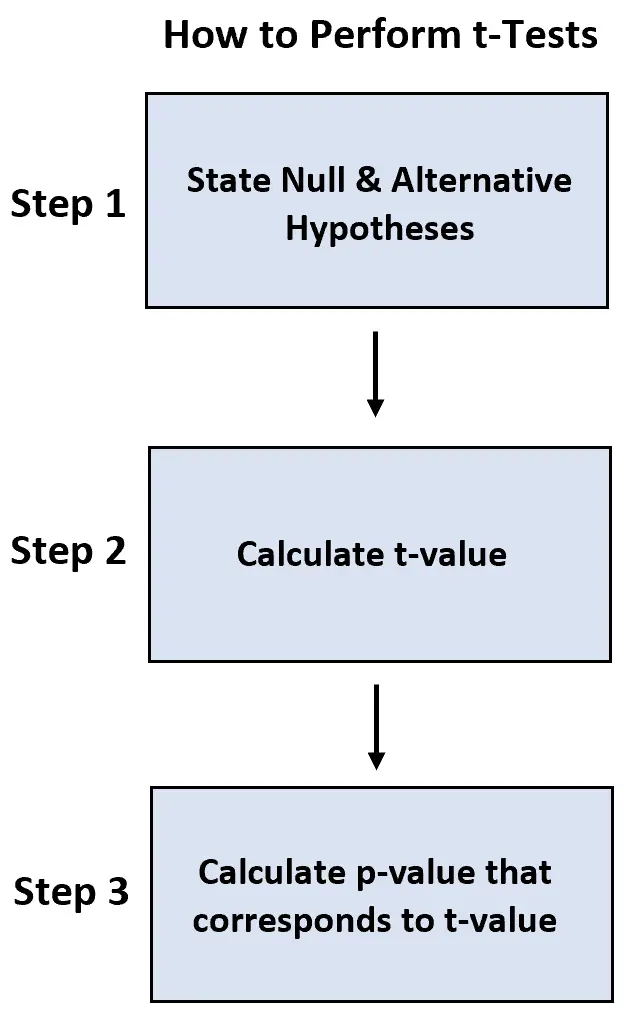
نستخدم الخطوات التالية لإجراء كل اختبار:
- الخطوة الأولى: اذكر الفرضية الصفرية والبديلة.
- الخطوة 2: احسب قيمة t.
- الخطوة 3: احسب القيمة p التي تتوافق مع القيمة t.
بالنسبة لكل اختبار، تكون قيمة t هي وسيلة لقياس الفرق بين متوسطات السكان والقيمة p هي احتمال الحصول على قيمة t بقيمة مطلقة كبيرة على الأقل كما لاحظنا بالفعل في “العينة”. البيانات إذا كانت الفرضية الصفرية صحيحة بالفعل.
إذا كانت القيمة p أقل من قيمة معينة (على سبيل المثال 0.05)، فإننا نرفض الفرضية الصفرية للاختبار.
بالنسبة لكل نوع من اختبارات t، نحن مهتمون بالقيمة p ونستخدم ببساطة قيمة t كخطوة وسيطة لحساب القيمة p.
يوضح المثال التالي كيفية حساب وتفسير قيمة t والقيمة p المقابلة لاختبار t المكون من عينتين.
مثال: حساب وتفسير قيم T وقيم P
لنفترض أننا نريد أن نعرف ما إذا كان متوسط وزن نوعين مختلفين من السلاحف متساويًا أم لا. قمنا بجمع عينة عشوائية بسيطة مكونة من 12 سلحفاة من كل مجموعة بالأوزان التالية:
الأنواع رقم 1 : 301، 298، 295، 297، 304، 305، 309، 298، 291، 299، 293، 304
الأنواع رقم 2 : 302، 309، 324، 313، 312، 310، 305، 298، 299، 300، 289، 294
فيما يلي كيفية إجراء اختبار t المكون من عينتين باستخدام هذه البيانات:
الخطوة الأولى: اذكر الفرضية الصفرية والبديلة.
أولاً سنذكر الفرضيتين الصفرية والبديلة:
- H 0 : μ 1 = μ 2 (متوسطا السكان متساويان)
- H 1 : μ 1 ≠ μ 2 (وسطا السكان غير متساويين)
الخطوة 2: احسب قيمة t.
بعد ذلك، سوف نقوم بإدخال أوزان كل عينة من السلاحف في آلة حاسبة اختبار t المكونة من عينتين ونجد أن قيمة t هي -1.608761 .
الخطوة 3: احسب القيمة الاحتمالية.
يمكننا أيضًا استخدام الآلة الحاسبة لاختبار t المكونة من عينتين للعثور على أن القيمة p التي تتوافق مع قيمة t البالغة -1.608761 هي 0.121926 .
وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم.
وهذا يعني أنه ليس لدينا أدلة كافية لنقول أن متوسط وزن السلاحف بين المجموعتين مختلف.
لاحظ أننا استخدمنا ببساطة قيمة t كخطوة وسيطة لحساب القيمة p. القيمة p هي القيمة الحقيقية التي كنا مهتمين بها، ولكن كان علينا حساب قيمة t أولاً.
مصادر إضافية
تقدم البرامج التعليمية التالية معلومات إضافية حول اختبارات t والقيم p:
مقدمة لاختبار t للعينة الواحدة
مقدمة لاختبار t ذو العينتين
مقدمة لاختبار t للعينات المقترنة
كيفية حساب قيمة P يدويًا من اختبار t
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر